




江西省九江市2022-2023学年高二下学期期末调研测试数学试题
展开![]() 江西省九江市2022-2023学年高二下学期期末调研测试数学试题
江西省九江市2022-2023学年高二下学期期末调研测试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知集合![]() ,则集合
,则集合![]() 的子集个数为( )
的子集个数为( )
A.1 B.2 C.4 D.8
2.已知命题![]() ,则
,则![]() 的否定是( )
的否定是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.函数![]() 的零点所在区间是( )
的零点所在区间是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.函数![]() 的部分图象大致为( )
的部分图象大致为( )
A.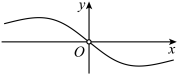 B.
B.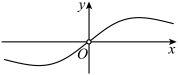
C.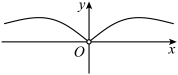 D.
D.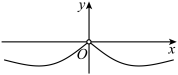
5.中国古代数学著作《九章算术》中有这样一个问题:“某贾人擅营,月入益功疾(注:从第2个月开始,每月比前一月多入相同量的铜钱),第3月入25贯,全年(按12个月计)共入510贯”,则该人第11月营收贯数为( )
A.64 B.65 C.68 D.70
6.设![]() ,则( )
,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.已知函数![]() ,当
,当![]() 时,恒有
时,恒有![]() ,则实数
,则实数![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.北京时间2023年2月10日0时16分,经过约7小时的出舱活动,神舟十五号航天员费俊龙、邓清明、张陆密切协同,圆满完成出舱活动全部既定任务,出舱活动取得圆满成功.载人飞船进入太空需要搭载运载火箭,火箭在发射时会产生巨大的噪声,已知声音的声强级![]() (单位:
(单位:![]() )与声强
)与声强![]() (单位:
(单位:![]() )满足关系式:
)满足关系式:![]() .若某人交谈时的声强级约为
.若某人交谈时的声强级约为![]() ,且火箭发射时的声强与此人交谈时的声强的比值约为
,且火箭发射时的声强与此人交谈时的声强的比值约为![]() ,则火箭发射时的声强级约为( )
,则火箭发射时的声强级约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、多选题
9.已知![]() ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.已知幂函数![]() ,则( )
,则( )
A.![]()
B.![]() 的定义域为
的定义域为![]()
C.![]()
D.将函数![]() 的图像向左平移
的图像向左平移![]() 个单位长度得到函数
个单位长度得到函数![]() 的图像
的图像
11.已知函数![]() ,则( )
,则( )
A.![]() 恰有2个极值点 B.
恰有2个极值点 B.![]() 在
在![]() 上单调递增
上单调递增
C.![]() D.
D.![]() 的值域为
的值域为![]()
12.提丢斯-波得定则是关于太阳系中行星轨道的一个简单的几何学规则,它是在1766年由德国的一位中学老师戴维·提丢斯发现的,后来被柏林天文台的台长波得归纳成一个经验公式来表示,即数列![]() :
:![]() ,表示的是太阳系第
,表示的是太阳系第![]() 颗行星与太阳的平均距离(以天文单位
颗行星与太阳的平均距离(以天文单位![]() 为单位).现将数列
为单位).现将数列![]() 的各项乘以10后再减4,得到数列
的各项乘以10后再减4,得到数列![]() ,可以发现数列
,可以发现数列![]() 从第3项起,每项是前一项的2倍,则下列说法正确的是( )
从第3项起,每项是前一项的2倍,则下列说法正确的是( )
A.数列![]() 的通项公式为
的通项公式为![]()
B.数列![]() 的第20项为
的第20项为![]()
C.数列![]() 的前10项和为157.3
的前10项和为157.3
D.数列![]() 的前
的前![]() 项和
项和![]()
三、填空题
13.已知函数![]() ,则
,则![]() 的图像在点
的图像在点![]() 处的切线的斜率为 .
处的切线的斜率为 .
14.已知![]() ,则
,则![]() 的值为 .
的值为 .
15.在中国,周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例,其中“弦”指的是直角三角形的斜边.现将两个全等的直角三角形拼接成一个矩形,若其中一个三角形“弦”的长度为![]() ,则该矩形周长的最大值为 .
,则该矩形周长的最大值为 .
四、双空题
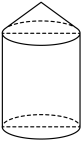
16.长征五号![]() 运载火箭是专门为中国载人航天工程空间站建设而研制的一款新型运载火箭,是中国近地轨道运载能力最大的新一代运载火箭,长征五号有效载荷整流罩外形是冯·卡门外形(原始卵形)+圆柱形,由两个半罩组成,某学校航天兴趣小组制作整流罩模型,模型近似看作一个圆柱和圆锥组成的几何体,如图所示,若圆锥的母线长为
运载火箭是专门为中国载人航天工程空间站建设而研制的一款新型运载火箭,是中国近地轨道运载能力最大的新一代运载火箭,长征五号有效载荷整流罩外形是冯·卡门外形(原始卵形)+圆柱形,由两个半罩组成,某学校航天兴趣小组制作整流罩模型,模型近似看作一个圆柱和圆锥组成的几何体,如图所示,若圆锥的母线长为![]() ,且圆锥的高与圆柱高的比为
,且圆锥的高与圆柱高的比为![]() ,则当圆锥的高为 时,该模型的体积取得最大值,且最大值为 .
,则当圆锥的高为 时,该模型的体积取得最大值,且最大值为 .
五、解答题
17.已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)记数列![]() 的前
的前![]() 项和为
项和为![]() ,求
,求![]() .
.
18.已知定义在![]() 上的函数
上的函数![]() 是偶函数.
是偶函数.
(1)求![]() 的值;
的值;
(2)求函数![]() 在其定义域上的最值.
在其定义域上的最值.
19.已知集合![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 及
及![]()
![]() ;
;
(2)若“![]() "是"
"是"![]() "成立的 ,求实数m的取值范围.
"成立的 ,求实数m的取值范围.
从“①充分不必要条件,②必要不充分条件”中任选一个,填在上面横线上并进行作答.注:如选择多个条件分别解答,按第一个解答计分.
20.已知函数![]() .
.
(1)求![]() 的极大值与极小值之差;
的极大值与极小值之差;
(2)若函数![]() 在区间
在区间![]() 上恰有2个零点,求
上恰有2个零点,求![]() 的取值范围.
的取值范围.
21.若数列![]() 满足
满足![]() ,则称数列
,则称数列![]() 为“平方递推数列".已知数列
为“平方递推数列".已知数列![]() 中,
中,![]() ,点
,点![]() 在函数
在函数![]() 的图象上,其中n为正整数,
的图象上,其中n为正整数,
(1)证明:数列![]() 是“平方递推数列”,且数列
是“平方递推数列”,且数列![]() 为等比数列;
为等比数列;
(2)设![]() ,
,![]() ,
,![]() 求数列
求数列![]() 的前10项和
的前10项和![]() .
.
22.已知函数![]() .
.
(1)当![]() 时,证明:
时,证明:![]() ;
;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求整数
恒成立,求整数![]() 的最小值.
的最小值.
2022-2023学年江西省南昌市部分学校高二下学期5月调研测试数学试题含答案: 这是一份2022-2023学年江西省南昌市部分学校高二下学期5月调研测试数学试题含答案,共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年江西省九江市高二第二次阶段模拟(期末)数学试题含答案: 这是一份2022-2023学年江西省九江市高二第二次阶段模拟(期末)数学试题含答案,共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
江西省九江市2022-2023学年高二数学下学期期末调研试题(Word版附解析): 这是一份江西省九江市2022-2023学年高二数学下学期期末调研试题(Word版附解析),共16页。试卷主要包含了 函数的部分图象大致为, 设,则, 已知幂函数,则等内容,欢迎下载使用。












