

2022-2023学年四川省成都市嘉祥重点学校高二(下)零诊数学试卷(文科)(含解析)
展开2022-2023学年四川省成都市嘉祥重点学校高二(下)零诊数学试卷(文科)
一、单选题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
1. 已知集合A={3,5,7,9,11,13,17},B={x|x=4n+1,n∈Z},则A∩B=( )
A. {5,9,11} B. {5,9,11,17} C. {5,13,17} D. {5,9,13,17}
2. 已知z+2−i=z(2+i),则复数z=( )
A. −12−32i B. 12−32i C. −32−32i D. 32−32i
3. 已知a=0.823,b=log923,c=40.3,则( )
A. a
A. 18π+12 B. 20π+12 C. 18π+16 D. 20π+16
5. 某高山地区的大气压强p(Pa)与海拔高度h(m)近似满足函数关系p=p0e−kh,其中k=0.000126,p0是海平面大气压强,已知在该地区甲、乙两处测得的大气压强分别为p1,p2,且p1p2=12,那么甲、乙两处的海拔高度之差约为( )
(参考数据:ln2≈0.693)
A. 4900m B. 5500m C. 6200m D. 7400m
6. 若函数f(x)=2x3−6x+a的图象与x轴有三个交点,则实数a的取值范围为( )
A. {−4,4} B. {4}
C. {a|a<−4或a>4} D. {a|−4
A. x−y−2=0 B. 2x−y−6=0 C. x+y−6=0 D. x−2y=0
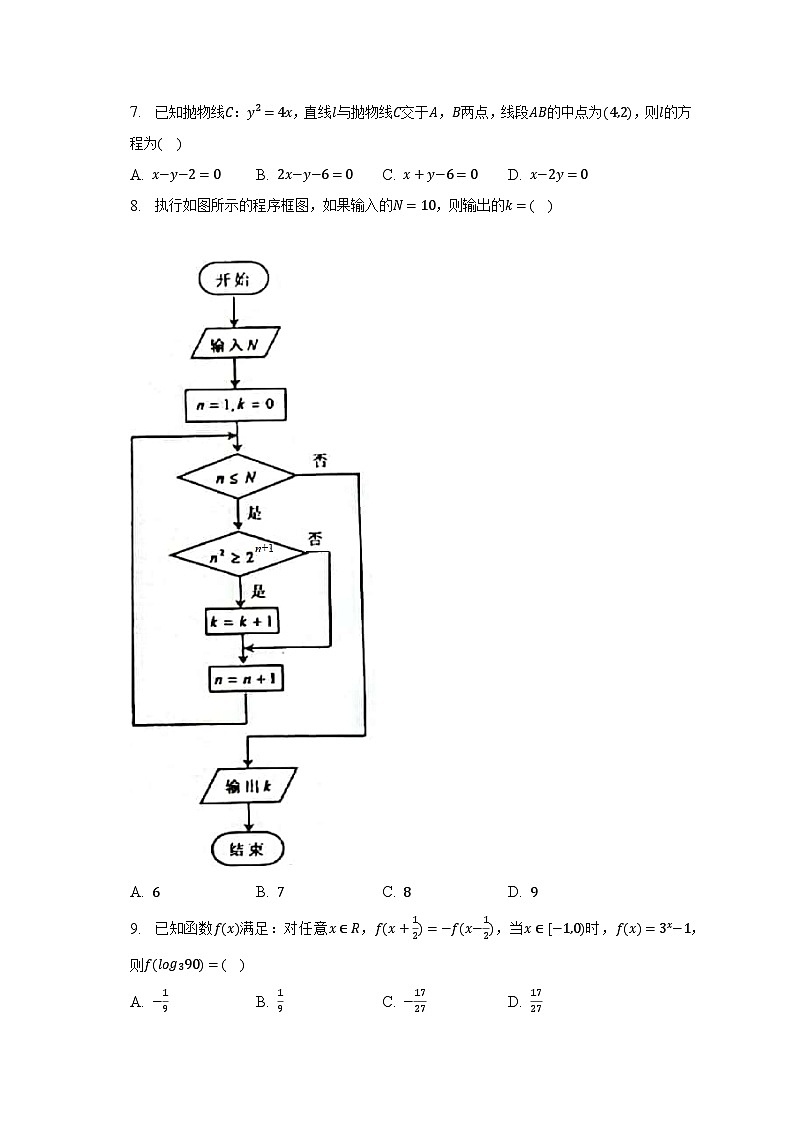
8. 执行如图所示的程序框图,如果输入的N=10,则输出的k=( )
A. 6 B. 7 C. 8 D. 9
9. 已知函数f(x)满足:对任意x∈R,f(x+12)=−f(x−12),当x∈[−1,0)时,f(x)=3x−1,则f(log390)=( )
A. −19 B. 19 C. −1727 D. 1727
10. 已知三棱锥S−ABC的体积为28 33,其外接球的体积为5003π,若AB=AC=4,∠BAC=120°,则线段SA的长度的最小值为( )
A. 8 B. 5 2 C. 6 D. 4 2
11. 已知双曲线C:x2a2−y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,过F1的直线与C的左、右两支分别于点M,N,且满足|F1N|=3|F1M|,△MNF2是等边三角形,则双曲线C的渐近线方程为( )
A. y=± 3x B. y=±2x C. y=± 6x D. y=± 7x
12. 如图,在四棱柱ABCD−A1B1C1D1中,底面ABCD为正方形,AA1⊥底面ABCD,AA1=2AB,M、N分别是棱BB1、DD1上的动点,且DN=B1M,则下列结论中正确的是( )
A. 直线AC与直线MN所成角的大小与点M的位置有关
B. 直线AD与直线MN所成角的最大值为π3
C. 直线A1C与直线MN可能异面
D. 三棱锥A1−C1MN的体积保持不变
二、填空题(本大题共4小题,共20.0分)
13. 2022年北京冬奥会自由式单板滑雪障碍追逐赛(SX),是每组4名选手在由各种地形障碍构成的赛道上竞速的比赛,由通过终点线的顺序决定排名,每组的前两名将晋级下一轮比赛.假设一组运动员技术水平相同,则运动员A,B同时晋级的概率为______.
14. 函数f(x)=(x−2)ex,x≥0−x−2,x<0的单调递减区间为______.
15. 若数据x1,x2,x3,x4,x5,x6,x7,x8,4,6的方差为5,则数据x1,x2,x3,x4,x5,x6,x7,x8,3,7的方差为______.
16. 已知函数f(x)=mlnx−2x3+4ex2−mx(m≥0),若f(x)在[1,+∞)上有零点,则实数m的取值范围为______ .
三、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题12.0分)
为迎接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取100名学生,将他们的竞赛成绩(满分为100分)分为6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],得到如图1所示的频率分布直方图.
(1)估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表),并估计这100名学生成绩的中位数(精确到0.01);
(2)在抽取的100名学生中,规定:竞赛成绩不低于80分为“优秀”,竞赛成绩低于80分为“非优秀”.
①请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“竞赛成绩是否优秀与性别有关”?
②求出等高条形图需要的数据,并画出等高条形图2(按图中“优秀”和“非优秀”所对应阴影线画),利用条形图判断竞赛成绩优秀与性别是否有关系?
2×2列联表
优秀
非优秀
合计
男生
10
女生
50
合计
100
参考公式及数据:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),n=a+b+c+d,
P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
18. (本小题12.0分)
已知函数f(x)=13x3−x2+2.
(1)讨论函数f(x)的单调性;
(2)求函数f(x)在区间[a,a+1](a>0)的最大值.
19. (本小题12.0分)
如图所示在直三棱柱ABC−A1B1C1中,AA1=6,△ABC是边长为4的等边三角形,D,E,F分别为棱B1C1,AA1,BB1的中点,点P在棱BC上,且BC=4CP.
(Ⅰ)证明:AP//平面DCE;
(Ⅱ)求点D到平面CEF的距离.
20. (本小题12.0分)
已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为12,其右焦点为F,点P(0,1),且|PF|= 2.
(Ⅰ)求C的方程;
(Ⅱ)过点P且斜率为k(k≠0)的直线l与椭圆C交于A,B两点,过A,B分别作y轴的垂线,垂足为M,N,直线AN与直线y=3交于点E,证明:B,M,E三点共线.
21. (本小题12.0分)
已知函数f(x)=(x+1)lnx+(a−3)x.
(1)若函数f(x)为增函数,求实数a的取值范围;
(2)若函数f(x)有两个极值点x1,x2(x1
22. (本小题10.0分)
在平面直角坐标系xOy中,曲线C1的参数方程为x=1+ty=t−6(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为ρ−3ρ=6sinθ−4cosθ.
(Ⅰ)求C1的普通方程和C2的直角坐标方程;
(Ⅱ)过C1上一点P作C2的一条切线l,切点为Q,当|PQ|最小时,求△C2PQ外接圆的参数方程.
答案和解析
1.【答案】D
【解析】解:∵集合A={3,5,7,9,11,13,17},B={x|x=4n+1,n∈Z},
∴当k=1,2,3,4时,B与A有交集,
∴A∩B={5,9,13,17}.
故选:D.
直接求交集即可得解.
本题考查交集及其运算,属基础题.
2.【答案】B
【解析】解:由z+2−i=z(2+i),
得z=2−i1+i=(2−i)(1−i)2=12−32i,
故选:B.
由复数的运算求解即可.
本题考查了复数的运算,属基础题.
3.【答案】D
【解析】解:∵0<0.823<0.80=1,
∴0
∴b
利用指数函数与对数函数的单调性及特值0,1比较三个数的大小即可.
本题考查三个数的大小比较的求法,是基础题,解题时要认真审题,注意对数函数和指数函数的性质的合理运用.
4.【答案】C
【解析】解:由三视图可知,该几何体是一个底面半径为2,高为4的圆柱体的34,
其表面积为π×22×34×2+2π×2×34×4+2×4×2=18π+16,
故选:C.
根据三视图判断出该几何体为圆柱体的34即可求解.
本题考查了由三视图还原几何体以及几何体表面积的计算,属于基础题.
5.【答案】B
【解析】解:记甲、乙两处的海拔高度分别为h1,h2,则由题可知:
p1p2=p0e−kh1p0e−kh2=e−k(h1−h2)=12,
则h1−h2=ln2k=0.6930.000126=5500m,
故选:B.
根据已知列式,由幂的运算化简,然后转化为对数式可得.
本题考查了指数的运算及指数与对数的转换,属于基础题.
6.【答案】D
【解析】解:f′(x)=6x2−6=6(x−1)(x+1),
所以当x∈(−∞,−1)和(1,+∞)时,f′(x)>0,f(x)单调递增,
当x∈(−1,1)时,f′(x)<0,f(x)单调递减,
故函数f(x)的极大值f(−1)=4+a,极小值f(1)=a−4,
函数f(x)=2x3−6x+a的图象与x轴有三个交点,
所以4+a>0a−4<0,得a∈(−4,4),
故选:D.
求出函数的导数,解关于导函数的不等式,求出函数的单调区间,求出函数的极值,根据图像和x轴交点的个数得到关于a的不等式,解出即可.
本题考查了函数的单调性,极值问题,考查导数的应用以及转化思想,是中档题.
7.【答案】A
【解析】解:设点A(x1,y1)、B(x2,y2),则y1+y2=4y1+y2=4,
若直线l⊥x轴,则线段AB的中点在x轴上,不合乎题意,
则直线l的斜率存在,
由已知y12=4x1y22=4x2,
两式作差可得(y1−y2)(y1+y2)=4(x1−x2),
所以,直线l的斜率为y1−y2x1−x2=4y1+y2=1,
因此,直线l的方程为y−2=x−4,
即x−y−2=0.
故选:A.
设点A(x1,y1),B(x2,y2),则x1+x2=8y1+y2=4,利用点差法可求得直线l的斜率,再利用点斜式可得出直线l的方程.
本题考查了直线与抛物线的位置关系,属于基础题.
8.【答案】A
【解析】解:执行程序框图,有N=10,n=1,k=0,满足条件n≤N;
满足条件n2≥2n−1,k=1,n=2,满足条件n≤N;
满足条件n2≥2n−1,k=2,n=3,满足条件n≤N;
满足条件n2≥2n−1,k=3,n=4,满足条件n≤N;
满足条件n2≥2n−1,k=4,n=5,满足条件n≤N;
满足条件n2≥2n−1,k=5,n=6,满足条件n≤N;
满足条件n2≥2n−1,k=6,n=7,满足条件n≤N;
不满足条件n2≥2n−1,n=8,满足条件n≤N;
不满足条件n2≥2n−1,n=9,满足条件n≤N;
不满足条件n2≥2n−1,n=10,满足条件n≤N;
不满足条件n2≥2n−1,n=11,满足条件n≤N;
输出k=6.
故选:A.
执行程序框图,写出每一次循环n,k的值,当n=11时,满足n≥N,可得输出k的值.
本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,考查运算求解能力,是基础题.
9.【答案】C
【解析】解:对任意x∈R,f(x+12)=−f(x−12),
所以f(x+1)=−f(x),f(x+2)=f(x),即函数的周期T=2,
当x∈[−1,0)时,f(x)=3x−1,
则f(log390)=f(log3109)=−f(log31027)=3log31027−1=1027−1=−1727.
故选:C.
由已知先求出函数的周期,然后结合对数的运算及周期把所求函数值的变量转化到已知区间上,代入结合对数恒等式可求.
本题主要考查了函数值的求解,体现了转化思想的应用,属于中档题.
10.【答案】B
【解析】解:如图,
O1是△ABC所在截面圆圆心O是球心,OO1⊥平面ABC,
SH⊥平面ABC,H为垂足,连接HA,HO1,
则SH⊥AH,SH⊥O1H,
则OO1//SH,AB=AC=4,∠BAC=120°,
则BC=2ABsin60°=4 3,
2O1A=BCsin∠BAC,O1A=4 32sin120°=4,
S△ABC=12×4×4×sin120°=4 3,
由VS−ABC=13S△ABC⋅SH,得SH=7,
由球体积V=43πR3,得43πR3=5003π,R=5,
即OS=OA=5,
OO1= OA2−O1A2= 52−42=3,
在直角梯形SOO1H中,O1H= OO12−(SH−OH)2=3,
即H在以O1为圆心,3为半径的圆上,
AHmin=AO1−O1H=4−3=1,
所以SAmin= 72+12=5 2,
故选:B.
作出三棱锥的高SH,O是球心,O1是△ABC所在截面圆圆心,由球体积求得球半径,由已知求得△ABC面积,截面圆O1的半径,由棱锥体积求得高SH,计算出O1H,得H点轨迹是圆,从而由点与圆的位置关系可求得AH的最小值,即得SA的最小值.
本题考查了几何体的外接球问题,属于中档题.
11.【答案】C
【解析】解:设|NF2|=m,
因为△MNF2是等边三角形,
所以|MN|=|MF2|=m,
由双曲线的定义知,|NF1|−|NF2|=2a,|MF2|−|MF1|=2a,
所以|NF1|=2a+m,|MF1|=m−2a,
因为|F1N|=3|F1M|,所以2a+m=3(m−2a),即m=4a,
在△MF1F2中,由余弦定理知,|F1F2|2=|MF1|2+|MF2|2−2|MF1|⋅|MF2|cos∠F1MF2,
所以4c2=(m−2a)2+m2−2(m−2a)⋅mcos120°=4a2+16a2+2m2+2⋅2a⋅4a⋅(−12),
即c2=7a2,
所以渐近线方程y=±bax=± c2a2−1x=± 6x.
故选:C.
设|NF2|=m,结合等边三角形的性质与双曲线的定义,推出m=4a,再在△MF1F2中,利用余弦定理,可得c2=7a2,而渐近线方程y=± c2a2−1x,代入运算,得解.
本题考查双曲线的定义与几何性质,还涉及余弦定理,考查逻辑推理能力和运算能力,属于中档题.
12.【答案】D
【解析】解:由题可知四棱柱ABCD−A1B1C1D1为正四棱柱,如下图,
由AC⊥DB,AC⊥DN,DB∩DN=D,可得AC⊥平面DBMN,所以AC⊥MN,与点M的位置无关,故A错误;
如下图作NP//DA交AA1于P,则∠PNM为所求角,
又PN⊥PM,则cos∠PNM=PNMN,MN最大时,cos∠PNM最小,∠PNM最大,
可求得cos∠PNMmin= 66≠12,∠PNMmax≠π3,故B错误;
由题易证四边形A1MCN为平行四边形,所以直线A1C与直线MN一定相交,故C错误;
如下图,VA1−C1MN=VM−C1A1N=VA−C1A1N=VN−C1A1A=VD−C1A1A为定值,故D正确.
故选:D.
确定AC与平面MNDB的位置关系可判定A;根据MN的变化情况,确定直线AD与直线MN所成角最大时的位置,求出余弦值即可判定B;确定直线A1M和CN位置关系即可判定C;求出三棱锥A1−C1MN的体积即可判定D.
本题考查了异面直线所成的角、三棱锥体积的计算,属于中档题.
13.【答案】16
【解析】解:设这4名运动员分别是A,B,C,D,
则分别有AB,AC,AD,BC,BD,CD6中基本事件,
满足运动员A,B同时晋级的概率P=16,
故答案为:16.
根据列举法求出满足条件的概率即可.
本题考查了古典概型问题,考查概率求值,是基础题.
14.【答案】(−∞,1)
【解析】解:当x<0时,f(x)=−x−2,在(−∞,0)上递减,
当x≥0时,f(x)=(x−2)ex,
则f′(x)=ex+(x−2)ex=(x−1)ex,
当0≤x<1时,f′(x)<0,所以f(x)在0,1)上递减,
综上,f(x)的单调递减区间为(−∞,1),
故答案为:(−∞,1).
利用导数求出f(x)=(x−2)ex,x≥0的单调区间,从而可求出函数的减区间.
本题考查了分段函数的单调性,属于中档题.
15.【答案】5.6
【解析】解:设数据x1,x2,x3,x4,x5,x6,x7,x8,4,6的平均数为x−,
由数据x1,x2,x3,x4,x5,x6,x7,x8,4,6的方差为5,
则110[(x1−x−)2+...+(x8−x−)2+(4−x−)2+(6−x−)2]=5,
又数据x1,x2,x3,x4,x5,x6,x7,x8,4,6的平均数与数据x1,x2,x3,x4,x5,x6,x7,x8,3,7的平均数相等,
则数据x1,x2,x3,x4,x5,x6,x7,x8,3,7的方差为110[(x1−x−)2+...+(x8−x−)2+(3−x−)2+(7−x−)2]=110[(x1−x−)2+...+(x8−x−)2+(4−x−)2+(6−x−)2+6]=5.6,
故答案为:5.6.
由平均数、方差的运算求解即可.
本题考查了平均数、方差的运算,属基础题.
16.【答案】[0,2e3e−1].
【解析】解:若f(x)=mlnx−2x3+4ex2−mx=0,则m⋅lnx−xx=2x2−4ex,
g(x)=lnx−xx且x≥1,g′(x)=1−lnxx2,
故[1,e)上g′(x)>0,(e,+∞)上g′(x)<0,
所以g(x)在[1,e)上单调递增,在(e,+∞)上单调递减,故g(x)≤g(e)=1−ee;
令h(x)=2x2−4ex(x≥1),
则由h′(x)=4x−4e>0,得x>e.
故在[1,e)上h′(x)<0,在(e,+∞)上h′(x)>0,
所以h(x)在[1,e)上单调递减,在(e,+∞)上单调递增,
故h(x)≥h(e)=−2e2;
要使f(x)在[1,+∞)上有零点,只需1−ee⋅m≥−2e2,可得0≤m≤2e3e−1,
即实数m的取值范围为:[0,2e3e−1].
故答案为:[0,2e3e−1].
将条件转化为m⋅lnx−xx=2x2−4ex在[1,+∞)上有解,令g(x)=lnx−xx、h(x)=2x2−4ex,并利用导数研究它们在[1,+∞)上的单调性和最值,注意最值对应的自变量,结合mg(x)max≥h(x)min即求m的范围.
本题考查了利用导数研究函数的零点问题,属于中档题.
17.【答案】解:(1)这100名学生的平均成绩:45×0.05+55×0.1+65×0.25+75×0.3+85×0.2+95×0.1=73,
设成绩的中位数为x,则根据频率分布直方图可知,有(0.05+0.1+0.25)+(x−70)×0.03=0.5,
解得x=70+103≈73.33.(或另解:(0.1+0.2)+(80−x)×0.03=0.5,解得x=80−302≈73.33).
(2)①根据表中已知数据和频率分布直方图得下表
优秀
非优秀
合计
男生
10
40
50
女生
20
30
50
合计
30
70
100
根据表中数据可得K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=100(300−800)250×50×30×70=10021≈4.762,
因为4.762<6.635,
所以没有99%的把握认为“竞赛成绩是否优秀与性别有关”.
②根据2×2列联表中数据可知,样本中男生优秀的频率为1050=20%,男生非优秀的频率为4050=80%;女生优秀的频率2050=40%,女生非优秀的频率为3050=60%,
画出等高条形图如图所示:
根据等高条形图,比较图中两个用斜纹实线所画条的高可以发现,女生样本中成绩优秀的频率明显高于男生样本中成绩优秀的频率,
因此可以认为竞赛成绩优秀与性别有关.
【解析】(1)根据已知条件,结合平均数和中位数的公式,即可求解.
(2)①结合独立性检验公式,即可求解,
②分别求出男生优秀的频率,男生非优秀的频率,女生优秀的频率,女生非优秀的频率,画出等高条形图,结合图形,即可求解.
本题主要考查独立性检验公式,考查计算能力,属于中档题.
18.【答案】解:(1)f′(x)=x2−2x=x(x−2),
当x<0或x>2时,f′(x)>0;
当0
(2)由(1)知当0
当1
①当1
所以f(x)max=f(a+1)=13a3−a+43.
综上所述,当0
本题考查利用导数研究函数的单调性与最值,考查学生的逻辑思维能力和运算能力,属中档题.
19.【答案】(Ⅰ)证明:如图,取BC的中点O,连接DO,取CD的中点Q,连接PQ,EQ.
∵BC=4CP,∴CP=PO,可得PQ//DO,PQ=12DO.
∵AE//DO,AE=12DO,∴PQ//AE,PQ=AE.
∴四边形AEQP为平行四边形,得EQ//AP,
∵EQ⊂平面DCE,AP⊄平面DCE,
∴AP//平面DCE;
(Ⅱ)解:连接DF,AO,可得AO=2 3.
∵BB1⊥平面ABC,AO⊂平面ABC,∴BB1⊥AO.
由已知可得AO⊥BC,而BB1∩BC=B,∴AO⊥平面BCC1B1.
∵S△DCF=6×4−12×4×3−12×2×3−12×6×2=9,
∴VE−DCF=13×AO×S△DCF=13×2 3×9=6 3.
∵EC=FC= 32+42=5,EF=4,
∴S△CEF=12× 52−22×4=2 21.
设点D到平面CEF的距离为d,
则由VD−CEF=VE−DCF,得13×2 21×d=6 3,
解得d=9 77.
故点D到平面CEF的距离为9 77.
【解析】(Ⅰ)取BC的中点O,连接DO,取CD的中点Q,连接PQ,EQ.证明四边形AEQP为平行四边形,得EQ//AP,再由直线与平面平行的判定可得AP//平面DCE;
(Ⅱ)连接DF,AO,可得AO=2 3.证明AO⊥平面BCC1B1.分别求出三角形DCF与三角形CEF的面积,再由等体积法求点D到平面CEF的距离.
本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了利用等体积法求点到平面的距离,是中档题.
20.【答案】(Ⅰ)解:设F(c,0)(c>0),由题意知ca=12,所以a=2c.
因为点P(0,1),且|PF|= c2+1= 2,解得c=1,
所以a=2,b= 3,
因此C的方程为x24+y23=1.
(Ⅱ)证明:由题意可知,直线l的方程为y=kx+1.
联立直线方程与椭圆方程可得(3+4k2)x2+8kx−8=0,
设A(x1,y1),B(x2,y2),则x1+x2=−8k3+4k2,x1x2=−83+4k2.
因为BN⊥y轴,所以N(0,y2),所以直线AN:y=y1−y2x1x+y2,
令y=3,得E(x1(3−y2)y1−y2,3).
因为AM⊥y轴,所以M(0,y1).
所以kEM−kBM=(3−y1)(y1−y2)x1(3−y2)−(y1−y2−x2)
=(y1−y2)[3−y1x1(3−y2)+1x2]=y1−y2x1x2(3−y2)[x2(3−y1)+x1(3−y2)]
=y1−y2x1x2(3−y2)[x2(3−kx1−1)+x1(3−kx2−1)]
=y1−y2x1x2(3−y2)[2(x2+x1)−2kx1x2]
=y1−y2x1x2(3−y2)[2×(−8k3+4k2)−2k×(−83+4k2)]=0,
所以B,M,E三点共线.
【解析】(Ⅰ)根据|PF|= 2可求c,根据离心率可求a,再根据a、b、c关系可求b,从而可求C的方程;
(Ⅱ)设A(x1,y1),B(x2,y2).联立l方程和椭圆方程得根与系数的关系,联立AN方程与y=3求出E的坐标,验证kEM−kBM=0即可证明B、M、E三点共线.
本题主要考查椭圆方程的求解,直线与圆锥曲线的位置关系,韦达定理及其应用等知识,属于中等题.
21.【答案】解:(1)f′(x)=lnx+1x+a−2,若函数f(x)为增函数,
则f′(x)≥0恒成立.g(x)=lnx+1x+a−2,g′(x)=1x−1x2=x−1x2,令g′(x)=0得x=1,
当x∈(0,1)时,g′(x)<0,g(x)单调递减;
当x∈(1,+∞)时,g′(x)>0,g(x)单调递增,故g(x)≥g(1)=a−1,因此a≥1.
故a∈[1,+∞);
证明:(2)由(1)知当a<1时,f′(1)=a−1<0,
当x→0时,f′(x)→+∞;当x→+∞时,f′(x)→+∞,
故0
将③代入f(x1)+f(x2)+x1+x2=x1lnx1+x2lnx2+lnx1+lnx2+(a−2)(x1+x2)得f(x1)+f(x2)+x1+x2=lnx1+lnx2−2,
即证lnx1+lnx2>0,即证x1x2>1.
①−②得lnx1x2=1x2−1x1,令t=x1x2∈(0,1),则x1=t−1lnt,x2=t−1tlnt,
即只需证t−1lnt⋅t−1tlnt>1,即证lnt− t+1 t>0.令g(t)=lnt− t+1 t,g′(t)=−( t−1)22t t<0,
故g(t)在区间(0,1)上单调递减,当t∈(0,1)时,g(t)>g(1)=0,命题得证.
【解析】(1)对函数求导,由于函数为增函数,则f′(x)≥0恒成立,再构造函数,求a的范围即可,
(2)函数有两个极值点,得出两个极值点的关系,再进行证明即可.
本题考查利用导数研究函数的极值,考查学生的运算能力,属于中档题.
22.【答案】解:(Ⅰ)曲线C1的参数方程为x=1+ty=t−6(t为参数),由消去t得C1的普通方程为x−y−7=0;
圆C2的极坐标方程为ρ−3ρ=6sinθ−4cosθ,
根据x=ρcosθ y=ρsinθ x2+y2=ρ2 ,整理得:ρ2−3=6ρsinθ−4ρcosθ,
所以x2+y2−3=6y−4x,
即C2的直角坐标方程为(x+2)2+(y−3)2=16.
(Ⅱ)由圆的切线的性质可知,
当C2P⊥l时,|C2P|最小,|PQ|也最小.
此时直线C2P的斜率为−1,因为C2(−2,3),
所以直线C2P的方程为x+y−1=0.
由得P(4,−3),
所以C2P的中点坐标为(1,0),|C2P|=6 2,
所以△C2PQ外接圆的参数方程为x=1+3 2cosαy=3 2sinα( α为参数).
【解析】(I)消去参数t即可得到C1的普通方程,利用极坐标和直角坐标的转化关系即可得到C2的直角坐标方程;
(II)由已知条件得|QP|= |C2P|2−|C2Q|2,则当|C2P|最小,|PQ|也最小,|C2P|最小时,C2P⊥l,即可求出直线C2P的方程,利用几何性质即可求出△C2PQ外接圆的参数方程.
本题考查极坐标方程及参数方程,考查学生的运算能力,属于中档题.
2022-2023学年四川省成都市高二(下)期末数学试卷(文科)(含解析): 这是一份2022-2023学年四川省成都市高二(下)期末数学试卷(文科)(含解析),共19页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
四川省成都市2022-2023学年高二下学期期末零诊测试文科数学试卷及答案: 这是一份四川省成都市2022-2023学年高二下学期期末零诊测试文科数学试卷及答案,文件包含数学文pdf、文科数学答案pdf等2份试卷配套教学资源,其中试卷共8页, 欢迎下载使用。
四川省成都市2022-2023高二下学期期末零诊文科数学试卷+答案: 这是一份四川省成都市2022-2023高二下学期期末零诊文科数学试卷+答案,共8页。












