

2022-2023学年四川省成都市高二(下)期末数学试卷(文科)(含解析)
展开2022-2023学年四川省成都市高二(下)期末数学试卷(文科)
一、单选题(本大题共12小题,共60.0分。在每小题列出的选项中,选出符合题目的一项)
1. 设集合A={x|x2−x−2<0},B={−2,−1,0,1,2},则A∩B=( )
A. {−2,0,1} B. {−1,0,1,2} C. {0,1} D. {1,2}
2. 命题“∃m∈N, m2+1∈N”的否定是( )
A. ∀m∉N, m2+1∈N B. ∀m∈N, m2+1∉N
C. ∃m∈N, m2+1∉N D. ∃m∉N, m2+1∈N
3. 双曲线x22-y2=1的渐近线方程是( )
A. y=±12x B. y=± 22x C. y=±2x D. y=± 2x
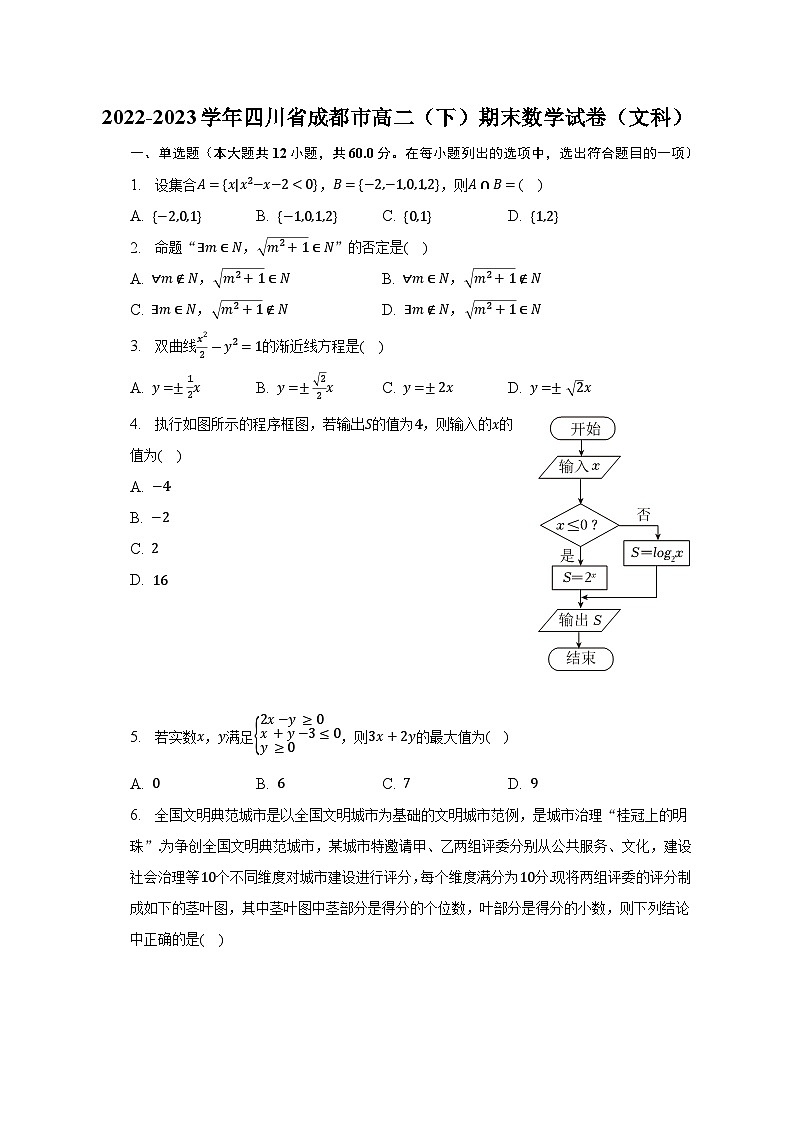
4. 执行如图所示的程序框图,若输出S的值为4,则输入的x的值为( )
A. −4
B. −2
C. 2
D. 16
5. 若实数x,y满足2x−y≥0x+y−3≤0y≥0,则3x+2y的最大值为( )
A. 0 B. 6 C. 7 D. 9
6. 全国文明典范城市是以全国文明城市为基础的文明城市范例,是城市治理“桂冠上的明珠”.为争创全国文明典范城市,某城市特邀请甲、乙两组评委分别从公共服务、文化,建设社会治理等10个不同维度对城市建设进行评分,每个维度满分为10分.现将两组评委的评分制成如下的茎叶图,其中茎叶图中茎部分是得分的个位数,叶部分是得分的小数,则下列结论中正确的是( )
A. 甲组评分的平均数小于乙组评分的平均数 B. 甲、乙两组评分的中位数不相同
C. 甲组评分的极差大于乙组评分的极差 D. 甲组评分的众数小于乙组评分的众数
7. 如图,在正方体ABCD−A1B1C1D1中,已知E,F,G,H分别是A1B1,AD,B1C1,C1D1的中点,则下列结论中错误的是( )
A. C,G,A1,F四点共面
B. 直线EF//平面BDD1B1
C. 平面HCG//平面BDD1B1
D. 直线EF和HG所成角的正切值为 2
8. 函数f(x)=ex−2023|x−2|的零点个数为( )
A. 0 B. 1 C. 2 D. 3
9. 已知直线l:mx+y−m=0(m∈R)和圆C:x2+y2−2x+4y+1=0,则“m=0”是“直线l与圆C相切”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
10. 七巧板又称七巧图,智慧板,是一种古老的中国传统智力玩具.据清代陆以湉《冷庐杂识》说:“宋黄伯思宴几图,以方几七,长段相参,衍为二十五体,变为六十八名.明严澈蝶几图,则又变通其制,以勾股之形,作三角相错形,如蝶翅.其式三,其制六,其数十有三,其变化之式,凡一百有余.近又有七巧图,其式五,其数七,其变化之式多至千余.体物肖形,随手变幻,盖游戏之具,足以排闷破寂,故世俗皆喜为之.”如图是一个用七巧板拼成的三角形(其中①②为两块全等的小型等腰直角三角形;③为一块中型等腰直角三角形;④⑤为两块全等的大型等腰直角三角形;⑥为一块正方形;⑦为一块平行四边形).现从该三角形中任取一点,则此点取自阴影部分的概率为( )
A. 18 B. 316 C. 14 D. 38
11. 记函数f(x)的导函数为f′(x).若f(x)为奇函数,且当时恒有f(x)cosx+f′(x)sinx>0成立,则( )
A. f(−π6)> 2f(−π4) B. f(π6)>− 3f(−π3)
C. 3f(π3)> 2f(π4) D. 2f(−π4)>− 3f(π3)
12. 如图①,已知四边形ABCD所有边长均为2,对角线AC=2 3.现以BD为折痕将四边形ABCD折起为四面体A′−BCD,使得A′D⊥BC,如图②.则四面体A′−BCD的外接球的表面积为( )
A. 23π B. 83π C. 6π D. 323π
二、填空题(本大题共4小题,共20.0分)
13. 已知复数z=(1−i)i(i为虚数单位),则|z|=______.
14. 第31届世界大学生夏季运动会将于2023年7月28日—8月8日在成都举行,比赛项目包括15个必选项目和武术、赛艇、射击3个自选项目,共18个大项,269个小项.小张、小王、小李三位大学生在谈论自己是否会武术、赛艇、射击3个自选项目时,小张说:我和小王都不会赛艇;小王说:我会的自选项目比小张多一个;小李说:三个自选项目中我们都会的项目只有一项,但我不会射击.假如他们三人都说的是真话,则由此可判断小张会的自选项目是______ (填写具体项目名称).
15. 已知P为抛物线y2=4x上的动点,F为抛物线的焦点,点Q(3, 5),则△PQF周长的最小值为______ .
16. 一条直线与函数y=lnx和y=ex的图象分别相切于点P(x1,y1)和点Q(x2,y2),则x2(x1−1)x1+1的值为______ .
三、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题12.0分)
记函数f(x)的导函数为f′(x),已知f(x)=x3+ax+10,f′(2)=0.
(1)求实数a的值;
(2)求f(x)在[−3,4]的值域.
18. (本小题12.0分)
某种产品的价格x(单位:万元/吨)与需求量y(单位:吨)之间的对应数据如表所示.
x
12
11
10
9
8
y
5
6
8
10
11
(1)已知可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程;
(2)请预测当该产品定价为6万元时需求量能否超过15吨?并说明理由.
参考公式:a=y−−bx−,b =i=1n(xi−x−)(yi−y−)i=1n(xi−x−)2.
19. (本小题12.0分)
如图,在直三棱柱ABC−A1B1C1中,已知AB⊥AC,AB=AC=4,AA1=2,D,E分别为棱AB,AC上的动点,F为BC中点,且BD=AE.
(Ⅰ)求三棱锥A−A1DE体积的最大值;
(Ⅱ)当三棱锥A−A1DE的体积最大时,求证:B1D⊥平面A1DF.
20. (本小题12.0分)
已知椭圆E:x2a2+y2b2=1(a>b>0)的离心率为12,椭圆E上的点到其左、右焦点的距离之和为4.
(1)求椭圆E的方程;
(2)设过左焦点F的直线l与椭圆E相交于A,B两点,M为AB的中点,O为坐标原点,若椭圆E上存在点N满足ON=λOM(λ>0),求四边形AOBN面积的最小值及此时λ的值.
21. (本小题12.0分)
已知函数f(x)=lnx+ax−a,其中a∈R.
(1)当a=1时,求函数f(x)的单调区间;
(2)当x>1时,若f(x)>−2恒成立,求整数a的最大值.
22. (本小题10.0分)
在平面直角坐标系xOy中,已知曲线C1的参数方程为x=2ty=t2(t为参数).以坐标原点O为极点,x轴非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρsinθ+ρcosθ=5.设曲线C1与曲线C2相交于A,B两点.
(1)求曲线C1的普通方程与曲线C2的直角坐标方程;
(2)已知点P(2,3),求1|PA|+1|PB|的值.
答案和解析
1.【答案】C
【解析】解:由x2−x−2<0,得(x+1)(x−2)<0,解得−1
故选:C.
先求出集合A,再求两集合的交集即可.
本题主要考查交集及其运算,属于基础题.
2.【答案】B
【解析】解:命题“∃m∈N, m2+1∈N”的否定是“∀m∈N, m2+1∉N”.
故选:B.
直接利用含有一个量词的命题的否定求解即可.
本题考查了命题的否定,涉及了含有一个量词的命题的否定,要掌握含有一个量词的命题的否定方法:改变量词,然后再否定结论.
3.【答案】B
【解析】
【分析】
本题考查双曲线的方程和性质,考查渐近线方程的求法,考查运算能力,属于基础题.
求出双曲线x22−y2=1的a,b,由双曲线x2a2−y2b2=1的渐近线方程为y=±bax,即可得到.
【解答】
解:双曲线x22−y2=1的a= 2,b=1,
由双曲线x2a2−y2b2=1的渐近线方程为y=±bax,
则所求渐近线方程为y=± 22x.
故选:B.
4.【答案】D
【解析】解:若2x=4,则x=2,此时不满足x≤0,不符合要求,故舍去,
若log2x=4⇒x=16,此时不满足x≤0,符合要求,故x=16.
故选:D.
根据程序框图,分类讨论求解.
本题主要考查程序框图的应用,属于基础题.
5.【答案】D
【解析】解:根据题意作可行域如图,
作直线l0:3x+2y=0,由图可知,平移直线l0到l位置,即过点B时,z取得最大值.
解方程组3x+2y=0y=0得B(3,0),
代入z=3x+2y=9.
故选:D.
先作可行域,再作直线l0:3x+2y=0,平移直线l0确定最优解,然后可得.
本题主要考查简单线性规划,考查转化能力,属于基础题.
6.【答案】A
【解析】解:甲的数据为7.5,7.6,7.8,7.9,8.0,8.1,8.3,8.3,8.5,8.6,乙组数据为7.5,7.6,7.8,7.8,8.0,8.1,8.2,8.3,8.5,9.8.
A选项,甲的平均数为:7.5+7.6+7.8+7.9+8.0+8.1+8.3+8.3+8.5+8.610=8.06,乙的平均数为:7.5+7.6+7.8+7.8+8.0+8.1+8.2+8.3+8.5+9.810=8.16,
甲的平均数小,A选项正确;
B选项,甲的中位数为:8.0+8.12=8.05,乙的中位数为:8.0+8.12=8.05,甲乙中位数一样,B选项错误;
C选项,甲的极差为1.1,乙的极差为2.3,甲的极差更小,C选项错误;
D选项,甲的众数为8.3,乙的众数为7.8,甲的众数更大,D选项错误.
故选:A.
根据茎叶图先写出甲乙两组数据,然后分别计算这两组数据的中位数,众数,极差,平均数.
本题主要考查茎叶图的应用,考查转化能力,属于中档题.
7.【答案】C
【解析】解:取BC中点M,连接B1M,FM,
由于F是AD的中点,在正方体中可知A1F//B1M,
又B1G=CM,B1G//CM,所以四边形B1GCM为平行四边形,故B 1M//CG,
因此CG//A1F,故C,G,A1,F四点共面,故A正确,
取AB中点N,连接FN,EN,
由于N,E,F均为中点,所以FN//BD,EN//BB1,
又因为FN⊄平面DBB1D1,BD平面DBB1D1,所以FN//平面DBB1D1,
同理EN//平面DBB1D1,EN∩FN=N,EN,FN⊂平面EFN,
所以平面EFN//平面DBB1D1,EF⊂平面EFN,故直线EF//平面BDD1B1,B正确,
假设平面HCG//平面BDD1B1,则平面HCG∩平面BCC1B1=GC,平面BDD1B1⋂平面BCC1B1=BB1,根据面面平行的性质可得平面BB1//GC,显然这与BB1与GC相交矛盾,故C错误,
由于GH//B1D1,BD//B1D1,FN//BD,所以GH//FN,
故∠EFN为直线EF和HG所成角或其补角,
不妨设正方体的棱长为a,则EN=a,FN= 2a2,
由于EN⊥底面ABCD,FN⊂平面ABCD,所以EN⊥FN,
故tan∠EFN=ENFN= 2,
直线EF和HG所成角的正切值为 2,D正确.
故选:C.
根据线线平行即可判断A,根据面面平行得线面平行即可判断B,根据面面平行的性质即可得矛盾判断C,根据异面直线的几何法找到其角,即可由三角形边角关系求解D.
本题主要考查了线面平行和面面平行的判定,考查了求异面直线所成的角,属于中档题.
8.【答案】D
【解析】解:f(x)=ex−2023|x−2|=ex−2023(x−2),x≥2ex+2023(x−2),x<2,
①当x≥2时,f(x)=ex−2023x+4046,则f′(x)=ex−2023,
由f′(x)>0,得x>ln2023,由f′(x)<0,得2≤x
所以f(x)在[2,+∞)上的最小值为f(ln2023)=eln2023−2023ln2023+4046=2023(3−ln2023)<0,
因为f(2)=e2−2023×2+4046=e2>0,
f(ln20232)=eln20232−2023ln20232+4046=2023(2025−2ln2023)>0,
所以f(x)在[2,ln2023)和(ln2023,+∞)上各有一个零点,
②当x<2时,f(x)=ex+2023x−4046,则f′(x)=ex+2023>0,
所以f(x)在(−∞,2)上递增,
因为f(2)=e2−2023×2+4046=e2>0,f(0)=e0−4046=−4045<0,
所以f(x)在(−∞,2)上有一个零点,
综上,f(x)共有3个零点.
故选:D.
先对函数化简得f(x)=ex−2023(x−2),x≥2ex+2023(x−2),x<2,然后分x≥2和x<2两种情况,利用导数和零点存在性定理讨论函数的零点即可.
此题考查函数与方程的综合问题,考查导数的应用,考查零点存在性定理的应用,解题的关键是利用导数求出函数的单调区间,然后结合零点存在性定理确定函数的零点,考查数学转化思想和计算能力,属于中档题.
9.【答案】C
【解析】解:圆C:x2+y2−2x+4y+1=0的方程可化为(x−1)2+(y+2)2=4,
其圆心坐标为(1,−2),半径为r=2,
当m=0时,直线l:y=0,圆心到直线的距离d=2=r,此时直线l与圆C相切,故充分性成立;
当直线l与圆C相切时,圆心到直线的距离d=|m−2−m| m2+12=r=2,所以m=0,故必要性成立,
所以“m=0”是“直线l与圆C相切”的充要条件.
故选:C.
根据充分条件和必要条件的判断方法,结合直线与圆的位置关系即可求解.
本题主要考查直线与圆的位置关系,属于基础题.
10.【答案】B
【解析】解:如图,
△ABC为等腰直角三角形,连接AD,EF,
由题可知,D,E,F,H,I 分别为BC,AB,AC,EF,FD的中点,
设BC=8,则AD=BD=4,AH=2,HI=FI= 2,GH=1,
则S△ABC=12×BC×AD=12×8×4=16,
阴影部分②的面积为12×HI×FI=12× 2× 2=1,
阴影部分⑦的面积为AH×GH=2×1=2
则从该三角形中任取一点,则此点取自阴影部分的概率为1+216=316.
故选:B.
数形结合,通过对图形的各点标记,以及各块几何图的性质,进行边长运算即可得出结论.
本题主要考查几何概型的应用,属于中档题.
11.【答案】B
【解析】解:令F(x)=f(x)sinx,
所以F′(x)=f(x)cosx+f′(x)sinx,
因为在(−π2,0)上,恒有f(x)cosx+f′(x)sinx>0成立,
所以任意x∈(−π2,0),F′(x)>0恒成立,
所以F(x)在(−π2,0)上单调递增,
因为f(x)为奇函数,
所以f(−x)=−f(x),
所以F(−x)=f(−x)sin(−x)=−f(x)⋅(−sinx)=f(x)sinx=F(x),
所以F(x)为偶函数,
所以F(x)在(0,π2)上单调递减
对于A:因为−π2>−π6>−π4>0,
所以F(−π6)>F(−π4),
所以f(−π6)sin(−π6)>f(−π4)sin(−π4),
所以−12f(−π6)>− 22f(−π4),
所以f(−π6)< 2f(−π4),故A错误;
对于B:因为F(x)为偶函数,
所以F(π6)=F(−π6),
因为−π2>−π6>−π3>0,
所以F(−π6)>F(−π3),
所以f(−π6)sin(−π6)>f(−π3)sin(−π3),
所以−12f(−π6)>− 32f(−π3),
所以f(−π6)< 3f(−π3),
所以−f(π6)< 3f(−π3),
所以f(π6)>− 3f(−π3),故B正确;
对于C:因为0<π4<π3<π2,
所以F(π4)>F(π3),
所以f(π4)sin(π4)>f(π3)sin(π3),
所以 22f(π4)> 32f(π3),
所以 2f(π4)> 3f(π3),故C错误;
对于D:由C知 2f(π4)> 3f(π3),
所以− 2f(−π4)> 3f(π3),
所以 2f(−π4)<− 3f(π3),故D错误;
故选:B.
令F(x)=f(x)sinx,求导F(x)的单调性,由奇偶性的定义,逐项分析,即可得出答案.
本题考查导数的综合应用,解题关键是分析函数的单调性,属于中档题.
12.【答案】C
【解析】解:由题意可知AB=BC=2,AC=2 3,由余弦定理可得cos∠ABC=AB2+BC2−AC22AB⋅BC=4+4−122×2×2=−12,
所以∠ABC=120°,故四边形ABCD为∠BCD=60°的菱形,
取BC中点为O,连接OD,OA′,
由于三角形BCD为等边三角形,所以BC⊥OD,
又A′D⊥BC,A′D∩OD=D,A′D,OD⊂平面A′OD,
所以BC⊥平面A′OD,A′O⊂平面A′OD,所以BC⊥A′O,
由于O为BC中点,所以A′B=A′C=2,故三角形A′BC为边长为2的等边三角形,
故A′B=A′C=A′D=BD=BC=CD=2,故四面体A′−BCD为棱长为2的正四面体,
不妨将其放入正方体中,则正方体的棱长为 22CB= 2,其正方体的外接球即为四面体的外接球,
则正方体的体对角线长为其外接球的一条直径,故2R= ( 2)2+( 2)2+( 2)2= 6,
故外接球的表面积为4πR2=6π.
故选:C.
根据边长可判断为四边形ABCD为菱形,进而根据线线垂直得线面垂直,可证得四面体A′−BCD为棱长为2的正四面体,将其放入正方体中,借助正方体的外接球即可求解.
本题主要考查球的表面积的求解,考查转化能力,属于中档题.
13.【答案】 2
【解析】解:z=(1−i)i=1+i,
∴|z|= 12+12= 2,
故答案为: 2.
利用复数模的计算公式即可求得复数z的模.
本题考查复数求模,属于基础题.
14.【答案】武术
【解析】解:由题意,如图下表所示:
武术
赛艇
射击
小张
会
不会
小王
会
不会
会
小李
会
不会
若他们三人都说的是真话,可得小张会武术,小王会武术和射击,小李会武术.
故答案为:武术.
根据题意,结合三人都说的是真话,利用表格的形式,即可求解.
本题主要考查简单的合情推理,属于基础题.
15.【答案】7
【解析】解:设点P在准线上的射影为D,则根据抛物线的定义可知|PF|=|PD|,
∴要求三角形周长的最小值,就是求解|PQ|+|PF|取得最小值,即求|PQ|+|PD|取得最小值.
当D,P,Q三点共线时|PQ|+|PD|最小,点Q(3, 5),|PQ|+|PF|的最小值为3−(−1)=4.
|QF|= (3−1)2+( 5−0)2=3,
则△PQF周长的最小值为:7.
故答案为:7.
设点P在准线上的射影为D,则根据抛物线的定义可知|PF|=|PD|进而把问题转化为求|PQ|+|PD|取得最小,进而可推断出当D,P,Q三点共线时|PQ|+|PD|最小,答案可得.
本题考查抛物线的定义、标准方程,以及简单性质的应用,判断当D,P,Q三点共线时|PQ|+|PD|最小,是解题的关键.
16.【答案】−1
【解析】解:因为f(x)=lnx,g(x)=ex,所以f′(x)=1x,g′(x)=ex,
则y=lnx在点P(x1,y1)处的切线方程为:y−lnx1=1x1(x−x1),即y=1x1x+lnx1−1;
y=ex在点Q(x2,y2)处的切线方程为:y−ex2=ex(x−x2),即y=exx+ex2(1−x2),
因为一条直线与函数y=lnx和y=ex的图象分别相切于点P(x1,y1)和点Q(x2,y2),
所以x1=1ex2lnx1−1=ex2(1−x2),则 −x2−1=1x1(1−x2),解得x2=1+x11−x1,
所以x2(x1−1)x1+1=−1.
故答案为:−1.
分别求得函数y=lnx和y=ex在点P(x1,y1)和点Q(x2,y2)处的切线方程,再由切线相同求解.
本题主要考查利用导数研究曲线上某点切线的方程,考查转化能力,属于中档题.
17.【答案】解:(1)由函数f(x)=x3+ax+10,可得f′(x)=3x2+a,
因为f′(2)=0,可得3×22+a=0,解得a=−12;
(2)由(1)得f′(x)=3x2−12=3(x+2)(x−2),
令f′(x)>0,解得x<−2或x>2;令f′(x)<0,解得−2
又由f(−3)=19,f(−2)=26,f(2)=−6,f(−3)=19,f(−2)=26,f(2)=−6,f(4)=26,
所以f(x)min=f(2)=−6,f(x)max=f(−2)=f(4)=26,
所以函数f(x)在[−3,4]的值域为[−6,26].
【解析】(1)求得f′(x)=3x2+a,根据f′(2)=0,列出方程,即可求解;
(2)由(1)得f′(x)=3(x+2)(x−2),求得f(x)的单调区间和最值,即可求得函数f(x)的值域.
本题主要考查利用导数研究函数的最值,考查转化能力,属于中档题.
18.【答案】解:(1)由题意得x−=15(12+11+10+9+8)=10,y−=15(5+6+8+10+11)=8;
因为i=15(xi−x−)(yi−y−)=2×(−3)+1×(−2)+(−1)×2+(−2)×3=−16,
i=15(xi−x−)2=22+12+(−1)2+(−2)2=10,
所以b =i=15(xi−x−)(yi−y−)i=15(xi−x−)2=−1.6,a =y−−b x−=24,
所以y关于x的线性回归方程为y =−1.6x+24;
(2)当x=6时,y =14.4<15;
所以当该产品定价为6万元时需求量不超过15吨.
【解析】(1)根据所给的数据求出利用最小二乘法所需要的几个数据,代入求系数b的公式中,求得结果,再把样本中心点代入公式,求出a的值,即可得到线性回归方程;
(2)根据(1)所求的线性回归方程,把x=6代入线性回归方程,即可解.
本题主要考查线性回归方程的应用,属于中档题.
19.【答案】(Ⅰ)解:设BD=AE=t,t∈(0,4),则AD=4−t,
所以三棱锥A−A1DE的体积为V=13S△ADE⋅A1A=13×12(4−t)t×2=13t(4−t),
当t=2时三棱锥A−A1DE的体积取得最大值为13×2×2=43;
(Ⅱ)证明:当三棱锥A−A1DE的体积最大时,AD=AE=2,
分别以AB、AC和AA1为x、y、z轴建立空间直角坐标系,如图所示:
则B1(4,0,2),D(2,0,0),F(2,2,0),A1(0,0,2),
所以B1D=(−2,0,−2),DF=(0,2,0),DA1=(−2,0,2),
计算B1D⋅DF=0,B1D⋅DA1=0,所以B1D⊥DF,B1D⊥DA1,
即B1D⊥DF,B1D⊥DA1,且DF∩DA1=D,DF⊂平面A1DF,DA1⊂平面A1DF,
所以B1D⊥平面A1DF.
【解析】(Ⅰ)设BD=AE=t,t∈(0,4),由此写出三棱锥A−A1DE的体积,利用函数的性质求出体积的最大值;
(Ⅱ)求出三棱锥A−A1DE的体积最大时AD=AE=2,建立空间直角坐标系,利用坐标表示向量,利用向量证明B1D⊥DF,B1D⊥DA1,即可证明B1D⊥平面A1DF.
本题考查了三棱锥体积计算问题,也考查了线面垂直的证明问题,是中档题.
20.【答案】解:(1)∵椭圆E的离心率为12,且椭圆E上的点到其左、右焦点距离之和为4,
∴ca=12且2a=4,解得a=2,c=1,
∴a2=4,b2=a2−c2=3,
∴椭圆E的标准方程为x24+y23=1.
(2)由题意知F(−1,0),直线l的斜率为0时显然不成立,
设直线l的方程为x=my−1,A(x1,y1),B(x2,y2),
由x=my−1x24+y23=1消去x,得(3m2+4)y2−6my−9=0,
Δ=144(m2+1)>0,则y1+y2=6m3m2+4,y1y2=−93m2+4,
∴y1+y22=3m3m2+4,∴y1+y22=3m3m2+4,x1+x22=my1−1+my2−12=−43m2+4,
∵M为AB的中点,∴M(−43m2+4,3m3m2+4),
∵ON=λOM,∵ON=λOM,∴N(−4λ3m2+4,3λm3m2+4),
又点N在椭圆E上,则(−4λ3m2+4)24+(3λm3m2+4)23=1,解得3m2+4=λ2,
∴S△AOB=12|OF||y1−y2|=12 (y1+y2)2−4y1y2=6 m2+13m2+4,
∵ON=λOM,
∴四边形AOBN的面积SAOBN=λS△AOB=6λ m2+13m2+4=6λ m2+1λ2=6 λ23−13λ=6 13−13λ2,
∵λ2=3m2+4≥4,
∴SAOBN=6 13−13λ2≥3(当且仅当λ=2时取等号),
∴当λ=2时,四边形AOBN面积最小值为3.
【解析】(1)利用椭圆离心率公式与定义求得a,b,c,从而得解;
(2)联立直线l与椭圆方程得到y1+y2,y1y2,从而求得S△AOB关于m的表达式,再利用ON=λOM得到SAOBN=λS△AOB,从而得解.
本题主要考查直线与椭圆的综合,考查转化能力,属于难题.
21.【答案】解:(1)当a=1时,函数f(x)=lnx+1x−1的定义域为(0,+∞),
f′(x)=1x−1x2=x−1x2(x>0).
由f′(x)>0解得x>1;由f′(x)<0解得0
(2)由题意当x>1时,f(x)>−2,即a(1−1x)
则g′(x)=x−lnx−3(x−1)2(x>1).
令h(x)=x−lnx−3(x>1).则h′(x)=1−1x.
当x>1时,h′(x)>0恒成立.
∴h(x)在(1,+∞)单调递增.
又h(4)=1−ln4<0,h(4)=1−ln4<0,h(5)=2−ln5>0,
∴∃x0∈(4,5),使得h(x0)=0,即lnx0=x0−3.
∴x∈(1,x0)时,h(x)<0;x∈(x0,+∞)时,h(x)>0.
∴g(x)在(1,x0)单调递减,在(x0,+∞)单调递增,
则gmin(x)=g(x0)=x0lnx0+2x0x0−1=x0(x0−3)+2x0x0−1=x0.
由a
【解析】(1)求得函数f(x)的定义域为(0,+∞),求得f′(x)=x−1x2,分别解不等式f′(x)<0、f′(x)>0可得出函数f(x)的单调递减区间和递增区间;
(2)分析可知不等式a
22.【答案】解:(1)由曲线C1的参数方程消去参数t,得曲线C1的的普通方程为x2=4y.
∵x=ρcosθ,y=ρsinθ,
化简得曲线C2的直角坐标方程为x+y−5=0.
(2)由题意得曲线C2的参数方程为x=2− 22my=3+ 22m(m为参数).
将其代入x2=4y,得m2−8 2m−16=0.
Δ=(8 2)2+64=192>0.
设A,B两点对应的参数分别为m1,m2.
则m1+m2=8 2,m1+m2=8 2,m1m2=−16.
则m1,m2为一正一负,
∴1|PA|+1|PB|=1|m1|+1|m2|=|m1|+|m2||m1||m2|=|m1−m2||m1||m2|= (m1+m2)2−4m1m2|m1m2|= 32.
【解析】(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.
(2)利用一元二次方程根和系数关系式的应用求出结果.
本题主要考查简单曲线的极坐标方程,考查转化能力,属于中档题.
2022-2023学年四川省成都市嘉祥重点学校高二(下)零诊数学试卷(文科)(含解析): 这是一份2022-2023学年四川省成都市嘉祥重点学校高二(下)零诊数学试卷(文科)(含解析),共18页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年四川省成都市树德中学高二(下)月考数学试卷(文科)(5月份)(含解析): 这是一份2022-2023学年四川省成都市树德中学高二(下)月考数学试卷(文科)(5月份)(含解析),共20页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年四川省成都市双流区名校高二(下)月考数学试卷(文科)(5月份)(含解析): 这是一份2022-2023学年四川省成都市双流区名校高二(下)月考数学试卷(文科)(5月份)(含解析),共20页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。












