






浙江省绍兴市2021-2023三年中考数学真题分类汇编
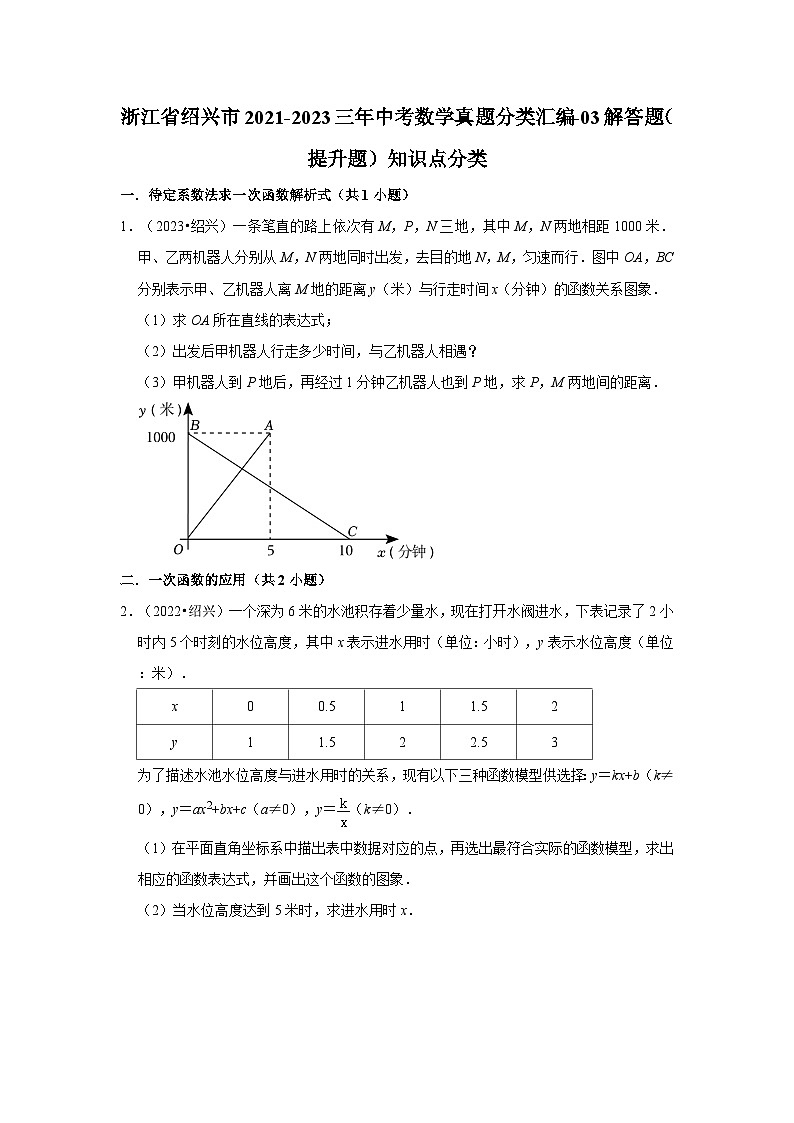
展开
这是一份浙江省绍兴市2021-2023三年中考数学真题分类汇编,文件包含浙江省绍兴市2021-2023三年中考数学真题分类汇编-03解答题提升题知识点分类doc、浙江省绍兴市2021-2023三年中考数学真题分类汇编-01选择题知识点分类doc、浙江省绍兴市2021-2023三年中考数学真题分类汇编-03解答题基础题知识点分类doc、浙江省绍兴市2021-2023三年中考数学真题分类汇编-02填空题知识点分类doc等4份试卷配套教学资源,其中试卷共90页, 欢迎下载使用。
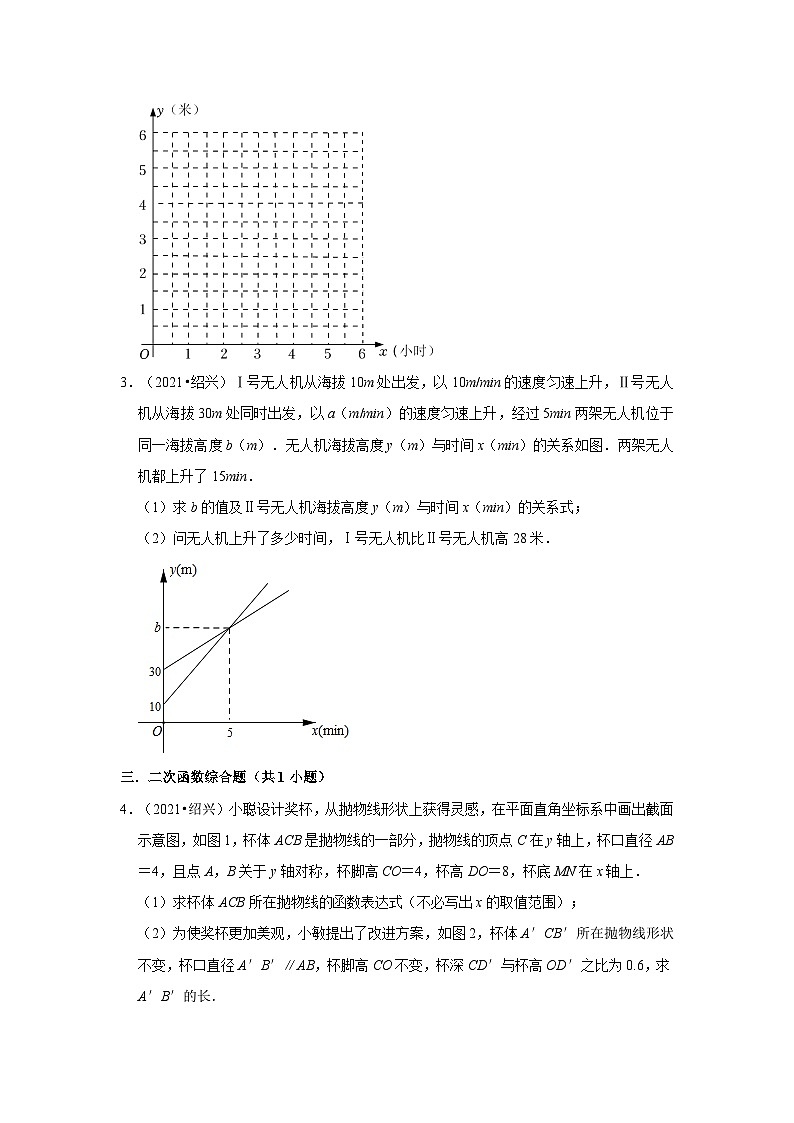
浙江省绍兴市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
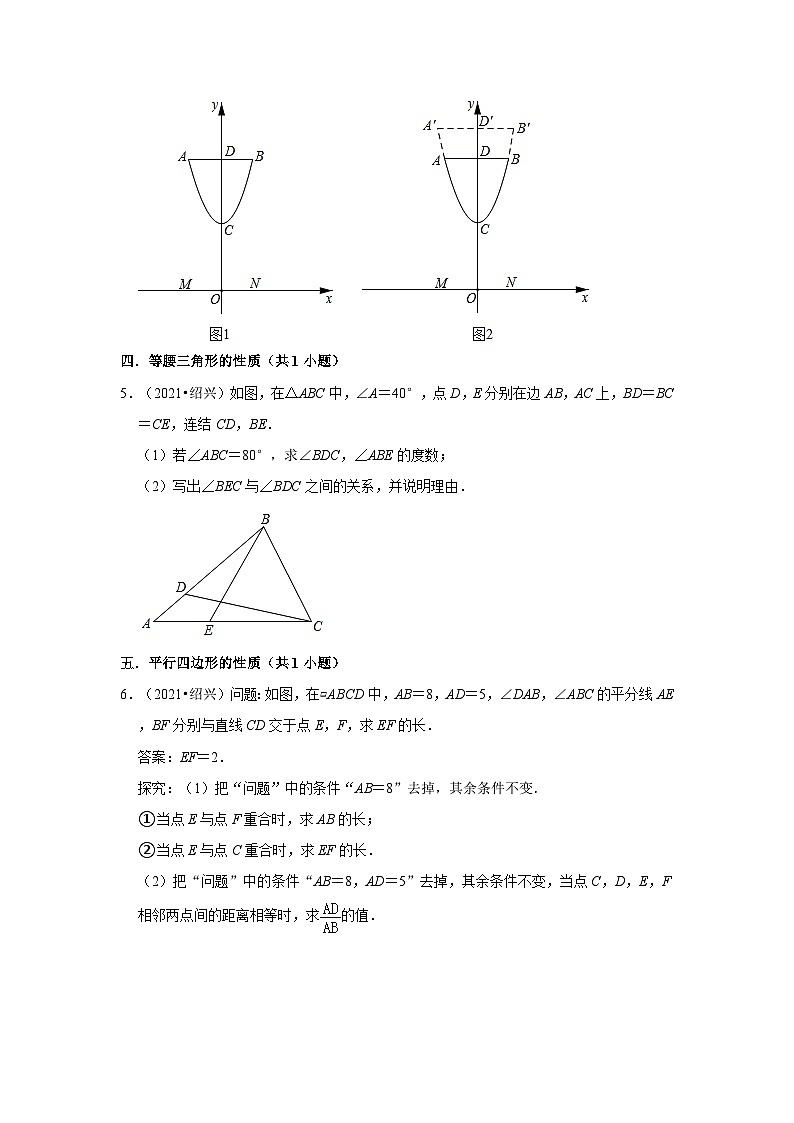
一.相反数(共1小题)
1.(2022•绍兴)实数﹣6的相反数是( )
A. B. C.﹣6 D.6
二.有理数的减法(共1小题)
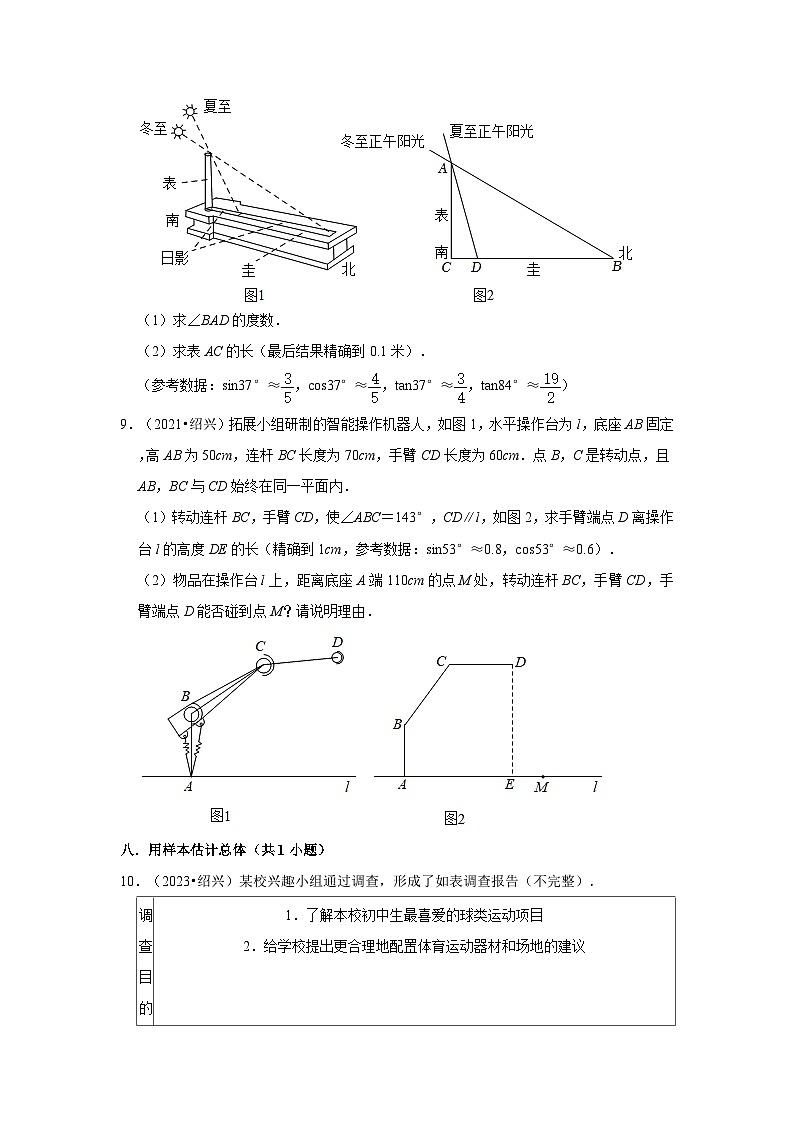
2.(2023•绍兴)计算2﹣3的结果是( )
A.﹣1 B.﹣3 C.1 D.3
三.科学记数法—表示较大的数(共3小题)
3.(2023•绍兴)据报道,2023年“五一”假期全国国内旅游出游合计274000000人次.数字274000000用科学记数法表示是( )
A.27.4×107 B.2.74×108 C.0.274×109 D.2.74×109
4.(2022•绍兴)2022年北京冬奥会3个赛区场馆使用绿色电力,减排320000吨二氧化碳.数字320000用科学记数法表示是( )
A.3.2×106 B.3.2×105 C.3.2×104 D.32×104
5.(2021•绍兴)第七次全国人口普查数据显示,绍兴市常住人口约为5270000人,这个数字5270000用科学记数法可表示为( )
A.0.527×107 B.5.27×106 C.52.7×105 D.5.27×107
四.实数大小比较(共1小题)
6.(2021•绍兴)实数2,0,﹣3,中,最小的数是( )
A.2 B.0 C.﹣3 D.
五.整式的除法(共1小题)
7.(2022•绍兴)下列计算正确的是( )
A.(a2+ab)÷a=a+b B.a2•a=a2
C.(a+b)2=a2+b2 D.(a3)2=a5
六.整式的混合运算(共1小题)
8.(2023•绍兴)下列计算正确的是( )
A.a6÷a2=a3 B.(﹣a2)5=﹣a7
C.(a+1)(a﹣1)=a2﹣1 D.(a+1)2=a2+1
七.由实际问题抽象出二元一次方程组(共1小题)
9.(2023•绍兴)《九章算术》中有一题:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大、小器各容几何?”译文:今有大容器5个,小容器1个,总容量为3斛(斛:古代容量单位);大容器1个,小容器5个,总容量为2斛,问大容器、小容器的容量各是多少斛?设大容器的容量为x斛,小容器的容量为y斛,则可列方程组是( )
A. B.
C. D.
八.函数的图象(共1小题)
10.(2023•绍兴)已知点M(﹣4,a﹣2),N(﹣2,a),P(2,a)在同一个函数图象上,则这个函数图象可能是( )
A. B.
C. D.
九.一次函数图象上点的坐标特征(共1小题)
11.(2022•绍兴)已知(x1,y1),(x2,y2),(x3,y3)为直线y=﹣2x+3上的三个点,且x1<x2<x3,则以下判断正确的是( )
A.若x1x2>0,则y1y3>0 B.若x1x3<0,则y1y2>0
C.若x2x3>0,则y1y3>0 D.若x2x3<0,则y1y2>0
一十.二次函数的性质(共2小题)
12.(2022•绍兴)已知抛物线y=x2+mx的对称轴为直线x=2,则关于x的方程x2+mx=5的根是( )
A.0,4 B.1,5 C.1,﹣5 D.﹣1,5
13.(2021•绍兴)关于二次函数y=2(x﹣4)2+6的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
一十一.直角三角形的性质(共1小题)
14.(2022•绍兴)如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( )
A.30° B.45° C.60° D.75°
一十二.菱形的性质(共1小题)
15.(2021•绍兴)如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC﹣CD方向移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
一十三.菱形的判定与性质(共1小题)
16.(2021•绍兴)数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形纵向排列放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是( )
A.用3个相同的菱形放置,最多能得到6个菱形
B.用4个相同的菱形放置,最多能得到16个菱形
C.用5个相同的菱形放置,最多能得到27个菱形
D.用6个相同的菱形放置,最多能得到41个菱形
一十四.正方形的性质(共1小题)
17.(2023•绍兴)如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD,AB的对称点为E1,E2;点F关于BC,CD的对称点为F1,F2在整个过程中,四边形E1E2F1F2形状的变化依次是( )
A.菱形→平行四边形→矩形→平行四边形→菱形
B.菱形→正方形→平行四边形→菱形→平行四边形
C.平行四边形→矩形→平行四边形→菱形→平行四边形
D.平行四边形→菱形→正方形→平行四边形→菱形
一十五.正方形的判定(共1小题)
18.(2022•绍兴)如图,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,边BC上的动点.下列四种说法:
①存在无数个平行四边形MENF;
②存在无数个矩形MENF;
③存在无数个菱形MENF;
④存在无数个正方形MENF.
其中正确的个数是( )
A.1 B.2 C.3 D.4
一十六.正多边形和圆(共1小题)
19.(2021•绍兴)如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
一十七.坐标与图形变化-平移(共1小题)
20.(2023•绍兴)在平面直角坐标系中,将点(m,n)先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )
A.(m﹣2,n﹣1) B.(m﹣2,n+1) C.(m+2,n﹣1) D.(m+2,n+1)
一十八.相似三角形的性质(共1小题)
21.(2022•绍兴)将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD,其中∠A=90°,AB=9,BC=7,CD=6,AD=2,则剪掉的两个直角三角形的斜边长不可能是( )
A. B. C.10 D.
一十九.相似三角形的判定与性质(共1小题)
22.(2023•绍兴)如图,在△ABC中,D是边BC上的点(不与点B,C重合).过点D作DE∥AB交AC于点E;过点D作DF∥AC交AB于点F、N是线段BF上的点,BN=2NF:M是线段DE上的点,DM=2ME.若已知△CMN的面积,则一定能求出( )
A.△AFE的面积 B.△BDF的面积 C.△BCN的面积 D.△DCE的面积
二十.相似三角形的应用(共1小题)
23.(2021•绍兴)如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5m,树影AC=3m,树AB与路灯O的水平距离AP=4.5m,则树的高度AB长是( )
A.2m B.3m C.m D.m
二十一.解直角三角形(共1小题)
24.(2021•绍兴)如图,Rt△ABC中,∠BAC=90°,cosB=,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连结CE,则的值为( )
A. B. C. D.2
二十二.简单组合体的三视图(共3小题)
25.(2023•绍兴)由8个相同的立方体搭成的几何体如图所示,则它的主视图是( )
A. B.
C. D.
26.(2022•绍兴)由七个相同的小立方块搭成的几何体如图所示,则它的主视图是( )
A. B. C. D.
27.(2021•绍兴)如图的几何体由五个相同的小正方体搭成,它的主视图是( )
A. B. C. D.
二十三.概率公式(共3小题)
28.(2023•绍兴)在一个不透明的袋子里装有2个红球和5个白球,它们除颜色外都相同,从中任意摸出1个球,则摸出的球为红球的概率是( )
A. B. C. D.
29.(2022•绍兴)在一个不透明的袋子里,装有3个红球、1个白球,它们除颜色外都相同,从袋中任意摸出一个球为红球的概率是( )
A. B. C. D.
30.(2021•绍兴)在一个不透明的袋中装有6个只有颜色不同的球,其中3个红球、2个黄球和1个白球.从袋中任意摸出一个球,是白球的概率为( )
A. B. C. D.
浙江省绍兴市2021-2023三年中考数学真题分类汇编-01选择题知识点分类
参考答案与试题解析
一.相反数(共1小题)
1.(2022•绍兴)实数﹣6的相反数是( )
A. B. C.﹣6 D.6
【答案】D
【解答】解:﹣6的相反数是6,
故选:D.
二.有理数的减法(共1小题)
2.(2023•绍兴)计算2﹣3的结果是( )
A.﹣1 B.﹣3 C.1 D.3
【答案】A
【解答】解:2﹣3=﹣1.
故选:A.
三.科学记数法—表示较大的数(共3小题)
3.(2023•绍兴)据报道,2023年“五一”假期全国国内旅游出游合计274000000人次.数字274000000用科学记数法表示是( )
A.27.4×107 B.2.74×108 C.0.274×109 D.2.74×109
【答案】B
【解答】解:274000000=2.74×108.
故选:B.
4.(2022•绍兴)2022年北京冬奥会3个赛区场馆使用绿色电力,减排320000吨二氧化碳.数字320000用科学记数法表示是( )
A.3.2×106 B.3.2×105 C.3.2×104 D.32×104
【答案】B
【解答】解:320000=3.2×105,
故选:B.
5.(2021•绍兴)第七次全国人口普查数据显示,绍兴市常住人口约为5270000人,这个数字5270000用科学记数法可表示为( )
A.0.527×107 B.5.27×106 C.52.7×105 D.5.27×107
【答案】B
【解答】解:5270000=5.27×106.
故选:B.
四.实数大小比较(共1小题)
6.(2021•绍兴)实数2,0,﹣3,中,最小的数是( )
A.2 B.0 C.﹣3 D.
【答案】C
【解答】解:∵﹣3<0<<2,
∴最小的数是﹣3,
故选:C.
五.整式的除法(共1小题)
7.(2022•绍兴)下列计算正确的是( )
A.(a2+ab)÷a=a+b B.a2•a=a2
C.(a+b)2=a2+b2 D.(a3)2=a5
【答案】A
【解答】解:A选项,原式=a2÷a+ab÷a=a+b,故该选项符合题意;
B选项,原式=a3,故该选项不符合题意;
C选项,原式=a2+2ab+b2,故该选项不符合题意;
D选项,原式=a6,故该选项不符合题意;
故选:A.
六.整式的混合运算(共1小题)
8.(2023•绍兴)下列计算正确的是( )
A.a6÷a2=a3 B.(﹣a2)5=﹣a7
C.(a+1)(a﹣1)=a2﹣1 D.(a+1)2=a2+1
【答案】C
【解答】解:A.a6÷a2=a4,故此选项不合题意;
B.(﹣a2)5=﹣a10,故此选项不合题意;
C.(a+1)(a﹣1)=a2﹣1,故此选项符合题意;
D.(a+1)2=a2+2a+1,故此选项不合题意.
故选:C.
七.由实际问题抽象出二元一次方程组(共1小题)
9.(2023•绍兴)《九章算术》中有一题:“今有大器五、小器一容三斛;大器一、小器五容二斛.问大、小器各容几何?”译文:今有大容器5个,小容器1个,总容量为3斛(斛:古代容量单位);大容器1个,小容器5个,总容量为2斛,问大容器、小容器的容量各是多少斛?设大容器的容量为x斛,小容器的容量为y斛,则可列方程组是( )
A. B.
C. D.
【答案】B
【解答】解:由题意得:,
故选:B.
八.函数的图象(共1小题)
10.(2023•绍兴)已知点M(﹣4,a﹣2),N(﹣2,a),P(2,a)在同一个函数图象上,则这个函数图象可能是( )
A. B.
C. D.
【答案】B
【解答】解:由N(﹣2,a),P(2,a)在同一个函数图象上,可知图象关于y轴对称,故选项A、C不符合题意;
由M(﹣4,a﹣2),N(﹣2,a),可知在y轴的左侧,y随x的增大而增大,故选项B符合题意;
故选:B.
九.一次函数图象上点的坐标特征(共1小题)
11.(2022•绍兴)已知(x1,y1),(x2,y2),(x3,y3)为直线y=﹣2x+3上的三个点,且x1<x2<x3,则以下判断正确的是( )
A.若x1x2>0,则y1y3>0 B.若x1x3<0,则y1y2>0
C.若x2x3>0,则y1y3>0 D.若x2x3<0,则y1y2>0
【答案】D
【解答】解:∵直线y=﹣2x+3,
∴y随x的增大而减小,当y=0时,x=1.5,
∵(x1,y1),(x2,y2),(x3,y3)为直线y=﹣2x+3上的三个点,且x1<x2<x3,
∴若x1x2>0,则x1,x2同号,但不能确定y1y3的正负,故选项A不符合题意;
若x1x3<0,则x1,x3异号,但不能确定y1y2的正负,故选项B不符合题意;
若x2x3>0,则x2,x3同号,但不能确定y1y3的正负,故选项C不符合题意;
若x2x3<0,则x2,x3异号,则x1,x2同时为负,故y1,y2同时为正,故y1y2>0,故选项D符合题意;
故选:D.
一十.二次函数的性质(共2小题)
12.(2022•绍兴)已知抛物线y=x2+mx的对称轴为直线x=2,则关于x的方程x2+mx=5的根是( )
A.0,4 B.1,5 C.1,﹣5 D.﹣1,5
【答案】D
【解答】解:∵抛物线y=x2+mx的对称轴为直线x=2,
∴﹣=2,
解得m=﹣4,
∴方程x2+mx=5可以写成x2﹣4x=5,
∴x2﹣4x﹣5=0,
∴(x﹣5)(x+1)=0,
解得x1=5,x2=﹣1,
故选:D.
13.(2021•绍兴)关于二次函数y=2(x﹣4)2+6的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
【答案】D
【解答】解:∵二次函数y=2(x﹣4)2+6,a=2>0,
∴该函数图象开口向上,有最小值,当x=4取得最小值6,
故选:D.
一十一.直角三角形的性质(共1小题)
14.(2022•绍兴)如图,把一块三角板ABC的直角顶点B放在直线EF上,∠C=30°,AC∥EF,则∠1=( )
A.30° B.45° C.60° D.75°
【答案】C
【解答】解:∵AC∥EF,∠C=30°,
∴∠C=∠CBF=30°,
∵∠ABC=90°,
∴∠1=180°﹣∠ABC﹣∠CBF=180°﹣90°﹣30°=60°,
故选:C.
一十二.菱形的性质(共1小题)
15.(2021•绍兴)如图,菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC﹣CD方向移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是( )
A.直角三角形→等边三角形→等腰三角形→直角三角形
B.直角三角形→等腰三角形→直角三角形→等边三角形
C.直角三角形→等边三角形→直角三角形→等腰三角形
D.等腰三角形→等边三角形→直角三角形→等腰三角形
【答案】C
【解答】解:∵∠B=60°,故菱形由两个等边三角形组合而成,
当AP⊥BC时,此时△ABP为直角三角形;
当点P到达点C处时,此时△ABP为等边三角形;
当P为CD中点时,△ABP为直角三角形;
当点P与点D重合时,此时△ABP为等腰三角形,
故选:C.
一十三.菱形的判定与性质(共1小题)
16.(2021•绍兴)数学兴趣小组同学从“中国结”的图案(图1)中发现,用相同的菱形纵向排列放置,可得到更多的菱形.如图2,用2个相同的菱形放置,得到3个菱形.下面说法正确的是( )
A.用3个相同的菱形放置,最多能得到6个菱形
B.用4个相同的菱形放置,最多能得到16个菱形
C.用5个相同的菱形放置,最多能得到27个菱形
D.用6个相同的菱形放置,最多能得到41个菱形
【答案】B
【解答】解:如图所示,
用2个相同的菱形放置,最多能得到3个菱形;
用3个相同的菱形放置,最多能得到8个菱形,
用4个相同的菱形放置,最多能得到16个菱形,
用5个相同的菱形放置,最多能得到29个菱形,
用6个相同的菱形放置,最多能得到47个菱形.
故选:B.
一十四.正方形的性质(共1小题)
17.(2023•绍兴)如图,在矩形ABCD中,O为对角线BD的中点,∠ABD=60°,动点E在线段OB上,动点F在线段OD上,点E,F同时从点O出发,分别向终点B,D运动,且始终保持OE=OF.点E关于AD,AB的对称点为E1,E2;点F关于BC,CD的对称点为F1,F2在整个过程中,四边形E1E2F1F2形状的变化依次是( )
A.菱形→平行四边形→矩形→平行四边形→菱形
B.菱形→正方形→平行四边形→菱形→平行四边形
C.平行四边形→矩形→平行四边形→菱形→平行四边形
D.平行四边形→菱形→正方形→平行四边形→菱形
【答案】A
【解答】解:如图1中,
∵四边形ABCD是矩形,
∴AB∥CD,∠BAD=∠ABC=90°,
∴∠BDC=∠ABD=60°,∠ADB=∠CBD=90°﹣60°=30°,
∵OE=OF、OB=OD,
∴DF=EB,
∵对称,
∴DF=DF2,BF=BF1,BE=BE2,DE=DE1,E1F2=E2F1.
∵对称
∴∠F2DC=∠CDF=60°,
∴∠EDA=∠E1DA=30°,
∴∠E1DB=60°,
同理∠F1BD=60°,
∴DE1∥BF1,
∵E1F2=E2F1,
∴四边形 E1E2F1F2 是平行四边形,
如图2所示,当E,F,O三点重合时,DO=OB,
∴DE1=DF2=AE1=AE2,即E1E2=E1F2,
∴四边形E1E2F1F2 是菱形.
如图3所示,当E,F分别为OD,OB的中点时,设DB=4,则 DF2=DF=1,DE1=DE=3,
在Rt△ABD中,AB=2,AD=2,连接AE,AO,
∵∠ABO=60°,BO=2=AB,
∴△ABO是等边三角形,
∵E为OB中点,
∴AE⊥OB,BE=1,
∴.
根据对称性可得 .
∴AD2=12,=9,=3,
∴,
∴ΔDE1A 是直角三角形,且∠E1=90°,
四边形E1E2F1F2是矩形.
当F,E分别与D,B重合时,△BE1D,△BDF1 都是等边三角形,则四边形 E1E2F2F2 是菱形,
∴在整个过程中,四边形 E1E2F1F2 形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形,
故选:A.
一十五.正方形的判定(共1小题)
18.(2022•绍兴)如图,在平行四边形ABCD中,AD=2AB=2,∠ABC=60°,E,F是对角线BD上的动点,且BE=DF,M,N分别是边AD,边BC上的动点.下列四种说法:
①存在无数个平行四边形MENF;
②存在无数个矩形MENF;
③存在无数个菱形MENF;
④存在无数个正方形MENF.
其中正确的个数是( )
A.1 B.2 C.3 D.4
【答案】C
【解答】解:连接AC,MN,且令AC,MN,BD相交于点O,
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵BE=DF,
∴OE=OF,
只要OM=ON,那么四边形MENF就是平行四边形,
∵点E,F是BD上的动点,
∴存在无数个平行四边形MENF,故①正确;
只要MN=EF,OM=ON,则四边形MENF是矩形,
∵点E,F是BD上的动点,
∴存在无数个矩形MENF,故②正确;
只要MN⊥EF,OM=ON,则四边形MENF是菱形,
∵点E,F是BD上的动点,
∴存在无数个菱形MENF,故③正确;
只要MN=EF,MN⊥EF,OM=ON,则四边形MENF是正方形,
而符合要求的正方形只有一个,故④错误;
故选:C.
一十六.正多边形和圆(共1小题)
19.(2021•绍兴)如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
【答案】B
【解答】解:连接OB、OC,如图,
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,
∴∠BPC=∠BOC=45°.
故选:B.
一十七.坐标与图形变化-平移(共1小题)
20.(2023•绍兴)在平面直角坐标系中,将点(m,n)先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是( )
A.(m﹣2,n﹣1) B.(m﹣2,n+1) C.(m+2,n﹣1) D.(m+2,n+1)
【答案】D
【解答】解:将点(m,n)先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是(m+2,n+1),
故选:D.
一十八.相似三角形的性质(共1小题)
21.(2022•绍兴)将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD,其中∠A=90°,AB=9,BC=7,CD=6,AD=2,则剪掉的两个直角三角形的斜边长不可能是( )
A. B. C.10 D.
【答案】A
【解答】解:如右图1所示,
由已知可得,△DFE∽△ECB,
则,
设DF=x,CE=y,
则,
解得,
∴DE=CD+CE=6+=,故选项B不符合题意;
EB=DF+AD=+2=,故选项D不符合题意;
如图2所示,
由已知可得,△DCF∽△FEB,
则,
设FC=m,FD=n,
则,
解得,
∴FD=10,故选项C不符合题意;
BF=FC+BC=8+7=15;
如图3所示:
此时两个直角三角形的斜边长为6和7;
故选:A.
一十九.相似三角形的判定与性质(共1小题)
22.(2023•绍兴)如图,在△ABC中,D是边BC上的点(不与点B,C重合).过点D作DE∥AB交AC于点E;过点D作DF∥AC交AB于点F、N是线段BF上的点,BN=2NF:M是线段DE上的点,DM=2ME.若已知△CMN的面积,则一定能求出( )
A.△AFE的面积 B.△BDF的面积 C.△BCN的面积 D.△DCE的面积
【答案】D
【解答】解:如图所示,连接ND,
∵DE∥AB,DF∥AC,
∴∠ECD=∠FDB,∠FBD=∠EDC,∠BFD=∠A,∠A=DEC.
∴△FBD∽△EDC,∠NFD=∠MEC.
∴=,
∵DM=2ME,BN=2NF,
∴,.
∴
∴,
又∵∠NFD=∠MEC,
∴△NFD∽△MEC.
∴∠ECM=∠FDN.
∵∠FDB=∠ECD,
∴∠MCD=∠NDB.
∴MC∥ND.
∴S△MNC=S△MDC.
∵DM=2ME,
∴.
故选:D.
二十.相似三角形的应用(共1小题)
23.(2021•绍兴)如图,树AB在路灯O的照射下形成投影AC,已知路灯高PO=5m,树影AC=3m,树AB与路灯O的水平距离AP=4.5m,则树的高度AB长是( )
A.2m B.3m C.m D.m
【答案】A
【解答】解:∵AB∥OP,
∴△CAB∽△CPO,
∴,
∴,
∴AB=2(m),
故选:A.
二十一.解直角三角形(共1小题)
24.(2021•绍兴)如图,Rt△ABC中,∠BAC=90°,cosB=,点D是边BC的中点,以AD为底边在其右侧作等腰三角形ADE,使∠ADE=∠B,连结CE,则的值为( )
A. B. C. D.2
【答案】D
【解答】解:设DE交AC于T,过点E作EH⊥CD于H.
∵∠BAC=90°,BD=DC,
∴AD=DB=DC,
∴∠B=∠DAB,
∵∠B=∠ADE,
∴∠DAB=∠ADE,
∴AB∥DE,
∴∠DTC=∠BAC=90°,
∵DT∥AB,BD=DC,
∴AT=TC,
∴EA=EC=ED,
∴∠EDC=∠ECD,
∵EH⊥CD,
∴CH=DH,
∵DE∥AB,
∴∠EDC=∠B,
∴∠ECD=∠B,
∴cos∠ECH=cosB=,
∴=,
∴==2,
故选:D.
二十二.简单组合体的三视图(共3小题)
25.(2023•绍兴)由8个相同的立方体搭成的几何体如图所示,则它的主视图是( )
A. B.
C. D.
【答案】D
【解答】解:如图所示:它的主视图是:
.
故选:D.
26.(2022•绍兴)由七个相同的小立方块搭成的几何体如图所示,则它的主视图是( )
A. B. C. D.
【答案】B
【解答】解:由图可得,
题目中图形的主视图是,
故选:B.
27.(2021•绍兴)如图的几何体由五个相同的小正方体搭成,它的主视图是( )
A. B. C. D.
【答案】D
【解答】解:从正面看,底层是三个小正方形,上层左边一个小正方形,
故选:D.
二十三.概率公式(共3小题)
28.(2023•绍兴)在一个不透明的袋子里装有2个红球和5个白球,它们除颜色外都相同,从中任意摸出1个球,则摸出的球为红球的概率是( )
A. B. C. D.
【答案】C
【解答】解:从中任意摸出1个球,则摸到红球的概率是:=,
故选:C.
29.(2022•绍兴)在一个不透明的袋子里,装有3个红球、1个白球,它们除颜色外都相同,从袋中任意摸出一个球为红球的概率是( )
A. B. C. D.
【答案】A
【解答】解:∵总共有4个球,其中红球有3个,摸到每个球的可能性都相等,
∴摸到红球的概率P=,
故选:A.
30.(2021•绍兴)在一个不透明的袋中装有6个只有颜色不同的球,其中3个红球、2个黄球和1个白球.从袋中任意摸出一个球,是白球的概率为( )
A. B. C. D.
【答案】A
【解答】解:∵袋子中共有6个小球,其中白球有1个,
∴摸出一个球是白球的概率是,
故选:A.
相关试卷
这是一份浙江省绍兴市2021-2023三年中考数学真题分类汇编-03解答题(提升题)知识点分类(含答案),共28页。试卷主要包含了的函数关系图象,的关系如图,问题等内容,欢迎下载使用。
这是一份浙江省绍兴市2021-2023三年中考数学真题分类汇编-03解答题(基础题)知识点分类(含答案),共18页。试卷主要包含了计算,0﹣,为4米等内容,欢迎下载使用。
这是一份2021-2023三年浙江省温州市中考数学真题分类汇编-03解答题(提升题)知识点分类(含答案),共29页。试卷主要包含了计算,某公司生产的一种营养品信息如表,根据以下素材,探索完成任务,,且∠AEB=∠CFD=90°,,且满足=,,连结AE等内容,欢迎下载使用。









