2023年广西梧州市中考数学二模试卷（含解析）

这是一份2023年广西梧州市中考数学二模试卷（含解析），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

2023年广西梧州市中考数学二模试卷
一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）
1. 5的相反数是(    )
A. 15 B. −5 C. ±5 D. −15
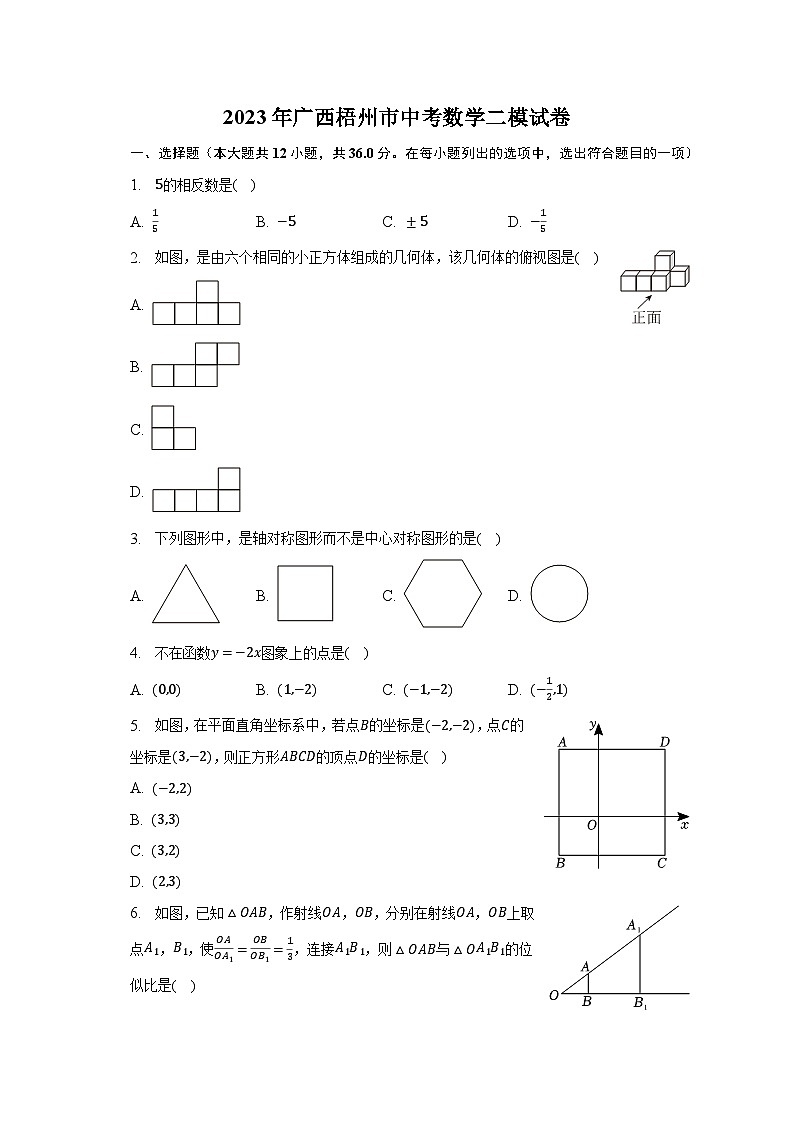
2. 如图，是由六个相同的小正方体组成的几何体，该几何体的俯视图是(    )
A.
B.
C.
D.
3. 下列图形中，是轴对称图形而不是中心对称图形的是(    )
A. B. C. D.
4. 不在函数y=−2x图象上的点是(    )
A. (0,0) B. (1,−2) C. (−1,−2) D. (−12,1)
5. 如图，在平面直角坐标系中，若点B的坐标是(−2,−2)，点C的坐标是(3,−2)，则正方形ABCD的顶点D的坐标是(    )
A. (−2,2)
B. (3,3)
C. (3,2)
D. (2,3)
6. 如图，已知△OAB，作射线OA，OB，分别在射线OA，OB上取点A1，B1，使OAOA1=OBOB1=13，连接A1B1，则△OAB与△OA1B1的位似比是(    )


A. 13 B. 23 C. 2 D. 3
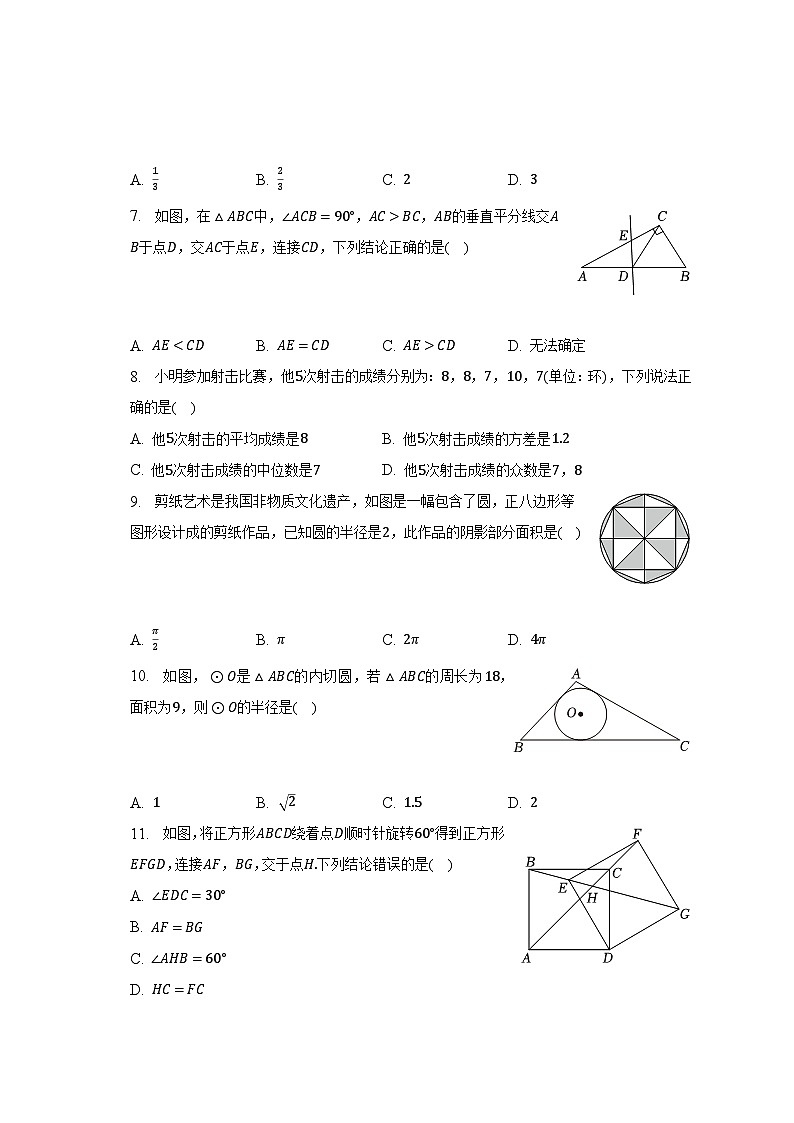
7. 如图，在△ABC中，∠ACB=90°，AC>BC，AB的垂直平分线交AB于点D，交AC于点E，连接CD，下列结论正确的是(    )


A. AECD D. 无法确定
8. 小明参加射击比赛，他5次射击的成绩分别为：8，8，7，10，7(单位：环)，下列说法正确的是(    )
A. 他5次射击的平均成绩是8 B. 他5次射击成绩的方差是1.2
C. 他5次射击成绩的中位数是7 D. 他5次射击成绩的众数是7，8
9. 剪纸艺术是我国非物质文化遗产，如图是一幅包含了圆，正八边形等图形设计成的剪纸作品，已知圆的半径是2，此作品的阴影部分面积是(    )


A. π2 B. π C. 2π D. 4π
10. 如图，⊙O是△ABC的内切圆，若△ABC的周长为18，面积为9，则⊙O的半径是(    )


A. 1 B. 2 C. 1.5 D. 2
11. 如图，将正方形ABCD绕着点D顺时针旋转60°得到正方形EFGD，连接AF，BG，交于点H.下列结论错误的是(    )
A. ∠EDC=30°
B. AF=BG
C. ∠AHB=60°
D. HC=FC
12. 如图，直线y=a(a是常数，a>0)与双曲线y=−4x(x<0)交于点A，与直线y=2x+4交于点B，当△OAB面积最小时，a的值是(    )
A. 1
B. 2
C. 3
D. 4
二、填空题（本大题共6小题，共12.0分）
13. 计算： 9= ______ ．
14. 分解因式：2x2−8= ______ ．
15. 一元二次方程(x−1)2=4的解为______ ．
16. 如图，在菱形ABCD中，点E，F分别是边BC，CD的中点，若AB=2，∠A=60°，则EF的长是______ ．


17. 如图，直线y1=−x+b与抛物线y2=12x2+2x−3相交于A，B两点，点B在y轴上，当y1>y2时，x的取值范围是______ ．


18. 如图，将矩形ABCD沿对角线BD折叠，点C落在点E处，若AB=4，AD=8，则点A到DE的距离是______ ．


三、解答题（本大题共8小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
19. (本小题9.0分)
计算：(−3)×2+|−4|−(−2)3．
20. (本小题9.0分)
解方程：−3x+12−x=1x−2−1．
21. (本小题9.0分)
菱形是一种富有美感的图形，小吴收到一块矩形的玉石ABCD，想尽可能制作成较大面积的菱形模型，在设计图纸上取AC作为这个菱形的对角线．
(1)请你用尺规作图的方法把这个菱形画出来(保留作图痕迹，不用写作法)；
(2)利用(1)中尺规作图过程中提供的条件证明你所作的图形是菱形．

22. (本小题9.0分)
综合实践
【问题情景】2022年4月21日，教育部正式印发《义务教育课程方案》，从2022年秋季开学起，劳动课将正式成为中小学的一门独立课程，并发布《义务教育劳动课程标准》，将煮饭、种菜、做手工、志愿服务等内容纳入其中.为了解学生劳动教育的情况，从某校学生中随机抽取了500名学生进行问卷调查．
【实践探究】该校开设“烹饪、种植、布艺、茶艺、木工”五门特色劳动校本课程学校要求每名学生必须选修且只能选修一门课程，为保证课程的有效实施，学校随机对抽取了500名学生选择课程情况调查，并将调查结果绘制成如下不完整的统计图．
【问题解决】请根据统计图提供的信息，解答下列问题：
(1)补全条形统计图，并在扇形统计图中，求出“种植”所对应的圆心角为多少度；
(2)若该校有1800名学生，请估计该校选择劳动课程为布艺的有多少人；
(3)在劳动课程中表现优异的小明和小华被选中与其他学生一起参加劳动技能展示表演，展示表演分为3个小组，他们俩若随机分到这三个小组中，请用列表或画树状图的方法求出小明和小华两人恰好分在同一组的概率．


23. (本小题9.0分)
要建一个面积为150m2的长方形养鸡场，为了节省材料，养鸡场的一边利用原有的一道墙，另三边用铁丝网围成，如果铁丝网的长为35m．
(1)若墙足够长，则养鸡场的长与宽各为多少？
(2)若给定墙长为am，则墙长a对题目的解是否有影响？
24. (本小题9.0分)
近年来，梧州市努力把六堡茶产业打造成乡村振兴的支柱产业，为庆祝2023年国际茶日，倡导茶为国饮，健康饮茶，助推做大六堡茶产业，打响六堡茶品牌和繁荣六堡茶经济，梧州市举办了“5.21国际茶日，邀你共饮六堡茶”系列活动.某商家借此活物也推出了某品牌两款茶叶的促销活动，已知A款茶叶每罐的进价比B款茶叶每罐的进价多40元，A款茶叶每罐售价300元，B款茶叶每罐售价250元.销售1罐A款茶叶和1罐B款茶叶的利润和为250元．
(1)求A，B两款茶叶的每罐进价分别是多少元？
(2)由于5月份的茶叶售卖情况良好，商家趁势而上，在电商平台“618”活动中，将A，B两款茶叶共400罐放到直播间进行售卖，其中A款茶叶的数量不少于160罐且不多于B款茶叶的数量.在茶叶的售价和进价都不变的情况下，每卖出1罐A款茶叶和1罐B款茶叶需给直播销售人员分别返还a元(a是常数)和0.5a元的提成.设本次在直播间销售的A款茶叶有x罐，售完所有茶叶后利润为w元.请求出w与x之间的函数关系式；当a=16时，求利润的最大值．
25. (本小题9.0分)
如图，⊙O是△ABC的外接圆，AB是⊙O的直径，△ABC与△ABD关于AB对称，点C的对应点为点D，DE//AB交⊙O于点E，连接AE交BD于点F.在C点作∠ACG=∠AED，交DA的延长线于点G．
(1)求证：AF=BF；
(2)求证：CG是⊙O的切线；
(3)若CG⊥DA，求EFAB的值．

26. (本小题9.0分)
如图，在平面直角坐标系中，O是坐标原点，抛物线y=ax2+bx−3与x轴交于A(−1,0)、B(3,0)，与y轴交于点C，其顶点为D点．
(1)求抛物线的解析式．
(2)连结BD、CD，动点Q的坐标为(m,1).P为抛物线上的一点，是否存在以B，D，Q，P为顶点的四边形是平行四边形？若存在，求出点P，Q的坐标；若不存在，请说明理由．
(3)连结OQ、CQ，当∠CQO最大时，求出点Q的坐标．


答案和解析

1.【答案】B 
【解析】解：根据概念，(5的相反数)+5=0，则5的相反数是−5．
故选：B．
据相反数的性质，互为相反数的两个数和为0，采用逐一检验法求解即可．
本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“−”号：一个正数的相反数是负数，一个负数的相反数是正数，0的相反数是0．

2.【答案】B 
【解析】解：该几何体的俯视图是．
故选：B．
根据几何体的俯视图是从几何体的上面看到的图形解答即可．
本题考查了几何体的三视图，属于基本题型，熟知几何体的俯视图是从几何体的上面看到的图形是解答本题的关键．

3.【答案】A 
【解析】解：A、是轴对称图形，不是中心对称图形，故本选项符合题意；
B、是轴对称图形，也是中心对称图形，故本选项不符合题意；
C、是轴对称图形，也是中心对称图形，故本选项不符合题意；
D、是轴对称图形，也是中心对称图形，故本选项不符合题意；
故选：A．
根据轴对称图形与中心对称图形的概念结合图形的形状求解．①如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．②如果一个图形绕某一点旋转180°后能够与自身重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．
本题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

4.【答案】C 
【解析】A.∵当x=0时，y=0，∴此点在函数图象上，不符合题意；
B.∵当x=1时，y=−2，∴此点在函数图象上，不符合题意；
C.∵当x=−1时，y=2≠−2，∴此点不在函数图象上，符合题意；
D.∵当x=−12时，y=1，∴此点在函数图象上，不符合题意．
故选：C．
分别把各点代入正比例函数的解析式进行检验即可．
本题考查了正比例函数图象上点的坐标特点，熟知正比例图象上各点的坐标一定合适此函数的解析式是解题的关键．

5.【答案】B 
【解析】解：∵点B的坐标是(−2,−2)，点C的坐标是(3,−2)，
∴BC//x，BC=3−(−2)=5，
∵四边形ABCD是正方形，
∴BC//AD，CD//AB，CD=BC=5，CD//y轴，
∴点D的坐标是(3,−2+5)，即(3,3)，
故选：B．
根据正方形的性质和坐标系中点的坐标特征进行求解即可．
此题考查了图形与坐标，熟练掌握正方形的性质和坐标系的特点是解题的关键．

6.【答案】A 
【解析】解：∵OAOA1=OBOB1=13，
∴△OAB与△OA1B1的位似比是13，
故选：A．
根据位似图形的定义，即可求解．
本题考查了位似的相关知识，掌握位似是相似的特殊形式，位似比等于相似比是解题的关键．

7.【答案】C 
【解析】解：∵AB的垂直平分线交AB于点D，
∴AD=BD，∠ADE=90°，
∵∠ACB=90°，
∴CD=12AB=AD，
∵AE>AD，
∴AE>CD，
故选：C．
根据线段垂直平分线的定义可得AD=BD，∠ADE=90°，根据直角三角形斜边中线的性质可得CD=12AB=AD，而AE>AD，则AE>CD，可得答案．
本题考查了线段垂直平分线的定义和直角三角形斜边中线的性质，熟知直角三角形斜边上的中线等于斜边的一半是解题的关键．

8.【答案】D 
【解析】解：他5次射击的成绩从小到大排列为：7，7，8，8，10，
A、他5次射击成绩的平均数，15(7+7+8+8+9)=7.8，故本选项不符合题意；
B、该组成绩数据的方差s2=15[2×(7−7.8)2+2×(8−7.8)2+(10−7.8)2]=1.24，故本选项不符合题意；
C、该组成绩的中位数是8，故本选项不符合题意；
D、∵7和8都出现了2次，出现的次数最多，
∴该组成绩的众数是7，8，故本选项符合题意．
故选：D．
根据众数、中位数、平均数和方差的意义分别对每一项进行分析，即可得出答案．
此题考查了平均数、中位数、众数和方差的意义，解题的关键是正确理解各概念的含义．

9.【答案】C 
【解析】解：由圆及正八边形的对称性可得：图中阴影部分的面积等于圆面积的一半，
所以此作品的阴影部分面积是12π×22=2π；
故选：C．
由圆及正八边形的对称性可得：图中阴影部分的面积等于圆面积的一半，据此即可求解．
本题考查了求阴影部分的面积，熟知圆及正八边形的对称性、得出阴影部分的面积等于圆面积的一半是解题的关键．

10.【答案】A 
【解析】解：如图，设⊙O与△ABC的各边分别相切于点E、F、G，连接OE，OF，OG，OA，OB，OC，设⊙O的半径为r，
则OE⊥AB，OF⊥AC，OG⊥BC，OE=OF=OG=r，
∵S△ABC=S△ABO+S△ACO+S△BOC，
=12AB⋅r+12AC⋅r+12BC⋅r，
=12(AB+AC+BC)⋅r，
又△ABC的周长为18，面积为9，
∴9=12×18⋅r，
∴r=1，
故选：A．

作辅助线如解析图，根据S△ABC=S△ABO+S△ACO+S△BOC，代入数据求解即可．
本题考查了利用三角形的面积求三角形的内切圆半径，掌握求解的方法是解题的关键．

11.【答案】D 
【解析】解：连接AE，CG，

∵将正方形ABCD绕着点D顺时针旋转60°得到正方形EFGD，
∴AD=DE，∠ADE=60°，
∴△ADE是等边三角形，
∴∠DAE=60°，
∴∠BAE=∠EDC=30°，故选项A正确；
连接BE，EG，
∵AB=AE，
∴∠AEB=12(180°−30°)=75°，∠DEG=45°，
∴∠BEA+∠AED+∠DEG=180°，
∴点E在线段BG上，同理点C在线段AF上，
∵AE=BC，∠AEF=60°+90°=∠BCG，EF=CG，
∴△AEF≌△BCG(SAS)，
∴AF=BG，故选项B正确；
∴∠AFE=∠BGC，
∵∠AHB=∠AFE+∠FEG=∠BGC+45°=∠BGC+∠DGE=60°，
故选项C正确；
不能证明HC=FC，故选项D不正确．
故选：D．
连接AE，CG，证明△ADE是等边三角形，推出点E在线段BG上，点C在线段AF上，证明△AEF≌△BCG，即可推出结论．
本题考查了正方形的性质，旋转的性质，等边三角形的判定和性质，全等三角形的判定和性质，等腰三角形的判定和性质，三角形内角和定理，熟记各图形的性质并准确识图是解题的关键．

12.【答案】B 
【解析】解：∵y=a，
∴a=−4xA，a=2xB+4，
∴xA=−4a，xB=12a−2，
∴AB=12a−2+4a，
∴S△OAB=12(12a−2+4a)⋅a=14a2−a+2=14(a2−4a+4−4)+2=14(a−2)2+1，
∵14>0，
∴当a=2时，S△OAB有最小值，最小值为1，
故选：B．
求得xA、xB，得到AB=12a−2+4a，利用三角形面积公式列式，根据二次函数的性质即可求解．
本题是反比例函数和一次函数的综合题，利用函数的解析式表示点的坐标，并表示线段的长，解题的关键是利用二次函数的性质解决问题．

13.【答案】3 
【解析】解： 9=3．
故答案为：3．
根据算术平方根的定义计算即可．
本题主要考查了算术平方根，掌握算术平方根的求法是解答本题的关键．

14.【答案】2(x+2)(x−2) 
【解析】解：2x2−8
=2(x2−4)
=2(x+2)(x−2)；
故答案为：2(x+2)(x−2)．
先提取公因数2，然后再运用平方差公式因式分解即可．
本题主要考查了因式分解，灵活运用提取公因式和公式法因式分解是解答本题的关键．

15.【答案】x1=3，x2=−1 
【解析】解：(x−1)2=4，
x−1=±2，
x1=3，x2=−1．
故答案为：x1=3，x2=−1．
根据直接开方法解一元二次方程，先进行开方，得到两个一元一次方程，再分别求解即可．
此题考查了直接开平方法解一元二次方程，解这类问题要移项，把所含未知数的项移到等号的左边，把常数项移项等号的右边，化成x2=a(a≥0)的形式，利用数的开方直接求解．

16.【答案】1 
【解析】解：连接BD，
∵四边形ABCD是菱形，
∴AB=AD，
∵∠A=60°，
∴△ABD是等边三角形，
∴BD=AB=2，
∵点E，F分别是边BC，CD的中点，
∴EF是△BCD的中位线，
∴EF=12BD=1，
故答案为：1．
利用菱形的性质求得△ABD是等边三角形，再利用三角形中位线定理求解即可．
本题考查了菱形的性质，等边三角形的判定和性质，三角形中位线定理，掌握“三角形的中位线平行于第三边且等于第三边的一半”是解题的关键．

17.【答案】−6 【解析】解：因为直线y1=−x+b与抛物线y2=12x2+2x−3分别交于A，B两点，
令x=0，则y2=−3，
∴B点坐标为(0,−3)，
则−3=−0+b，解得b=−3，
∴直线的解析式为y1=−x−3，
解方程−x−3=12x2+2x−3，
得x1=0，x2=−6，
∴A，B两点的横坐标分别为−6，0，
∴当y1>y2时，−6 故答案为：−6 求得A，B两点的横坐标，再根据图象得出取值范围即可．
此题考查二次函数与不等式，关键是根据图象得出取值范围．

18.【答案】245 
【解析】解：如图，作AG⊥DE交DE的延长线于点G，

∵矩形ABCD，
∴BC=AD=8，
由翻折的性质得，∠1=∠2，∠BED=∠C=90°，
∴BE=BC=8(角平分线的性质)，
∴EF//AG，
∵矩形ABCD的边AD//BC，
∴∠1=∠3，
∴∠2=∠3，
∴BF=DF，
∵AD=8，
∴AF=8−DF，
在Rt△ABF中，AB2+AF2=BF2，
∴42+(8−DF)2=DF2，
解得DF=5．
则EF=BE−BF=8−5=3，
∵EF//AG，
∴△DEF∽DGA，
∴EFAG=DFAD，即3AG=58，
∴AG=245，
故答案为：245．
根据翻折的性质可得∠1=∠2，再根据两直线平行，内错角相等可得∠2=∠3，再根据等角对等边可得BF=DF，在Rt△ABF中，利用勾股定理列出方程求得DF=5，证明△DEF∽DGA，利用相似三角形的性质即可求解．
本题考查了翻折变换的性质，相似三角形的判定和性质，平行线的性质，矩形的性质，勾股定理的应用，熟练掌握折叠的性质是解题的关键．

19.【答案】解：(−3)×2+|−4|−(−2)3
=−6+4−(−8)
=−6+4+8
=6． 
【解析】先计算乘法、绝对值和有理数的乘方，再计算加减．
本题考查了有理数的混合运算，掌握有理数的混合运算顺序：先算乘方，再算乘除，最后计算加减，如果有括号，先计算括号里面的是关键．

20.【答案】解：方程两边同乘以(x−2)，得3x−1=1−(x−2)，
解这个方程，得x=1，
经检验：x=1是方程的解；
∴原方程的解是：x=1． 
【解析】方程两边同乘以(x−2)，去掉分母化为整式方程，求得方程的解后再检验即得答案．
本题考查了分式方程的求解，属于基础题型，熟练掌握解分式方程的方法是解题的关键．

21.【答案】(1)解：如图，四边形AFCE即为所求菱形，

(2)证明：设AC与EF相交于点O，
由作图可知，直线EF垂直平分AC，
∴AO=CO，
∵四边形ABCD是矩形，
∴AB//CD，
∴∠OCE=∠OAF，
∵∠AOF=∠COE，
∴△AOF≌△COE(ASA)，
∴AF=CE，
∴四边形AFCE是平行四边形，
∵EF垂直AC，
∴四边形AFCE是菱形． 
【解析】(1)分别以点A和点C为圆心，以大于12AC为半径画弧，得到两个交点，过两个交点作直线EF，分别交CD、AB于点E和点F，则四边形AFCE即为所求菱形；
(2)设AC与EF相交于点O，由作图可知，直线EF垂直平分AC，则AO=CO，由 四边形ABCD是矩形得到AB//CD，则∠OCE=∠OAF，又由∠AOF=∠COE，可证得△AOF≌△COE(ASA)，则AF=CE，得到四边形AFCE是平行四边形，即可得到结论．
此题考查了菱形的判定、矩形的性质、三角形全等的判定和性质、垂直平分线的性质和作图等知识，熟练掌握相关性质和判定是解题的关键．

22.【答案】(1)解：选择“布艺”的学生人数为：
500−40−175−125−100=60(人)，
补全条形统计图，如图所示：

“种植”所对应的圆心角为：
360°×125500=90°．
(2)解：1800×60500=216(人)，
答：该校选择劳动课程为布艺的有216人．
(3)解：设三个小组分别为A、B、C，画树状图，如图所示：

∵共有9种等可能的情况，小明和小华两人恰好分在同一组的情况数有3种，
∴小明和小华两人恰好分在同一组的概率为39=13． 
【解析】(1)用总的调查人数减去另外4项的人数，即可得出“布艺”的学生人数，补全条形统计图即可；用360°×“种植”的百分比即可得出“种植”所对应的圆心角度数；
(2)用1800乘以选择劳动课程为布艺的百分比即可得出答案；
(3)根据题意画出树状图，然后求出概率即可．
本题主要考查了条形统计图和扇形统计图的信息关联，列表或画树状图求概率，用样本估计总体，解题的关键是数形结合，画出树状图．

23.【答案】解：(1)设垂直于墙的边长为xm，则平行于墙的边长为(35−2x)m，
依题意，得：x(35−2x)=150，
整理，得：2x2−35x+150=0，
解得：x1=7.5，x2=10，
∴35−2x=20或35−2x=15．
答：养鸡场的长为20m或15m，宽为7.5m或10m．
(2)当a<15时，题目无解；
当15≤a<20时，题目只有一个解；
当a≥20时，题目有两个解． 
【解析】(1)设垂直于墙的边长为xm，则平行于墙的边长为(35−2x)m，根据长方形的面积公式结合养鸡场的面积为150m2，即可得出关于x的一元二次方程，解之即可得出结论；
(2)根据(1)的结论可分a<15、15≤a<20及a≥20三种情况，找出题目解的个数．
本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．

24.【答案】解：(1)设B款茶叶的每罐进价为a元，则A款茶叶的每罐进价为b元，
由题意得300−b+250−a=250 b=a+40 ，
解得a=130 b=170
答：B款茶叶的每罐进价为130元，则A款茶叶的每罐进价为170元；
(2)设5月份A款茶叶的数量为x罐，
由题意得x≥160x≤400−x，
解得160≤x≤200，
∵W与x之间的函数关系为W=(300−170)a−ax+(400−x)(250−130)−0.5a(400−x)，
化简得W=(10−a2)x+48000−200a，
当a=16时，W=2x+44800
∵2>0，
∴W随x的增大而增大，
∴当x=200时，W有最大值，即W=200×2+44800=45200(元)，
综上，当a=16时，利润最大值为45200元． 
【解析】(1)设B款茶叶的每罐进价为a元，则A款茶叶的每罐进价为b元，根据题意列二元一次方程组，解之即可；
(2)由题意列出不等式组求出A款销售数量的范围，再写出利润与销售量之间的函数关系式，利用一次函数的性质求解即可．
本题考查一次函数的应用、二元一次方程组的应用、一元一次不等式组等知识，找到合适的等量关系及不等关系是解决问题的关键．

25.【答案】(1)证明：∵DE//AB，
∴∠DEF=∠FAB，
∵∠DEF=∠ABF，
∴∠FAB=∠FBA，
∴AF=BF；

(2)证明：连接OC，

∵AB是⊙O的直径，
∴∠ACB=90°，
∵△ABC与△ABD关于AB对称，点C的对应点为点D，
∴∠ACB=∠ADB=90°，∠ABC=∠ABD，
∵∠AED=∠ABD，
∴∠AED=∠ABC，
∵OC=OB，
∴∠OCB=∠OBC，
∴∠ACG=∠OCB=∠FAB=∠FBA，
∵∠ACO+∠OCB=90°，
∴∠ACO+∠ACG=∠OCG=90°，
∴半径OC⊥CG，
∴CG是⊙O的切线；

(3)解：连接OF，

∵CG⊥DA，
∴∠AGC=90°，
∴∠ACG+∠CAG=90°，
∵∠FAB=∠FBA，∠ABC=∠ABD，
∴∠FAB=∠CBA，
∴AE//BC，
∴∠EAC+∠ACB=180°，
∴∠EAC=180°−90°=90°，
∴∠CAG+∠DAF=180°−∠CAE=90°，
∴∠ACG=∠DAF，
∵∠ACG=∠FAB=∠FBA=∠DEF，
∴∠DAE=∠FBA=∠DEA=13×180°×12=30°，
∵AF=BF，AO=BO，
∴FO⊥AB，
∴∠AOF=90°，
∵tan∠FAO=FOAO，
∴tan30°=FOAO= 33，
∵AO=12AB，
∴FO12AB= 33，
∴FOAB= 36，
在△ADF和△AOF中，
∠ADF=∠AOF=90°∠DAF=∠OAF=30°AF=AF，
∴△ADF≌△AOF(AAS)，
∴DF=OF，
∵∠EDB=∠EAB，∠ABD=∠AED=∠EAB，
∴∠EDF=∠DEF，
∴FD=FE，
∴EF=OF，
∴EFAB= 36． 
【解析】(1)根据两直线平行内错角相等，在同圆中同弧所对的圆周角相等，三角形中等角对等边解答；
(2)根据直径所对的圆周角是直角得到∠ACB=90°，再利用轴对称图形的对应角相等得出∠ADB=90°，∠ABC=∠ABD，结合已知条件利用同角的余角相等得出∠OCB=∠ACG，再根据经过半径的外端且垂直于半径的直线是圆的切线解答即可；
(3)根据垂直的定义结合上面两个小题得出的结论得出∠DAE=∠FBA=∠DEA=30°，再利用等腰三角形三线合一得出∠AOF=90°，进而利用直角三角形三角函数得出FOAB= 36，再利用“AAS”及前面得出的结论得出EF=OF据此解答即可．
本题考查了切线的判定，圆周角定理，勾股定理，垂径定理，解直角三角形等知识，解题的关键是灵活运用所学知识解决问题．

26.【答案】解：(1)∵抛物线y=ax2+bx−3与x轴交于A(−1,0)、B(3,0)，
∴a−b−3=09a+3b−3=0，
解得a=1b=−2，
∴抛物线的解析式为y=x2−2x−3；
(2)∵y=x2−2x−3=(x−1)2−4，
∴D(1,−4)，
当DQ为对角线时，根据平行四边形的性质，相当于BD向上平移1个单位，
∵D(1,−4)，B(3,0)，
点B向上平移1个单位为点Q，
∴点D向上平移1个单位为点P，则点P的纵坐标为−3，
解方程x2−2x−3=−3，得x=0或x=2；
当x=0时，P(0,−3)，即点D(1,−4)向上平移1个单位，向左平移1个单位，
∴点B(3,0)向上平移1个单位，向左平移1个单位，得到点Q(2,1)，
当x=2时，同理P(2,−3)，Q(4,1)；
即P(0,−3)，Q(2,1)或P(2,−3)，Q(4,1)；
当DP为对角线时，根据平行四边形的性质，相当于BD向上平移5个单位，
∵B(3,0)，
∴点P的纵坐标为5，
解方程x2−2x−3=5，得，x=−2或x=4；
同理得P(−2,5)，Q(−4,1)或P(4,5)，Q(2,1)；
综上，P(0,−3)，Q(2,1)或P(2,−3)，Q(4,1)或P(−2,5)，Q(−4,1)或P(4,5)，Q(2,1)；
(3)如图，记△OQC的外心为M，则M在OC的垂直平分线MN上(设MN与y轴交于点N)．

连接OM、CM，则∠CQO=12∠CMO=∠OMN，MC=MO=MQ，
∴sin∠CQO=sin∠OMN=ONOM，
∴sin∠CQO的值随着OM的增大而减小．
又∵MO=MQ，
∴当MQ取最小值时sin∠CQO最大，
即MQ垂直直线y=1时，∠CQO最大，
此时，⊙M与直线y=1相切．
∴MQ=NF=2.5，MN= OM2−ON2=2，
∴Q坐标为(2,1)．
根据对称性，另一点(−2,1)也符合题意．
综上可知，Q点坐标为(2,1)或(−2,1)． 
【解析】(1)利用待定系数法即可求解；
(2)求得顶点D(1,−4)，分两种情况讨论，当DQ为对角线时，当DP为对角线时，根据平行四边形的性质以及平移的性质即可求解；
(3)记△OQC的外心为M，则M在OC的垂直平分线MN上(设MN与y轴交于点N)，连接OM、CM.由圆周角定理和三角函数的定义可表示出sin∠CQO，可得出sin∠CQO的值随着OM的增大而减小，则可得⊙M与直线y=1相切，再结合勾股定理可求得Q点的坐标．
本题主要考查二次函数的综合应用，涉及待定系数法、二次函数的性质、平行四边形的性质、直线和圆的位置关系、三角函数的定义等知识点．在(3)确定出∠CQO最大时⊙M与直线y=1相切是解题的关键．本题考查知识点较多，综合性较强．