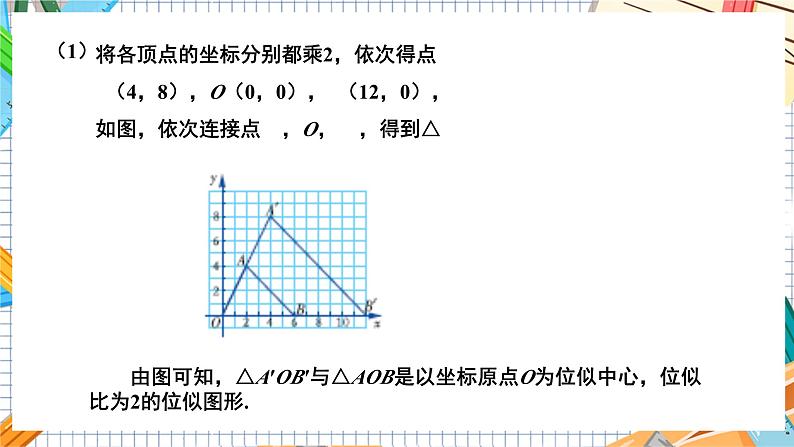
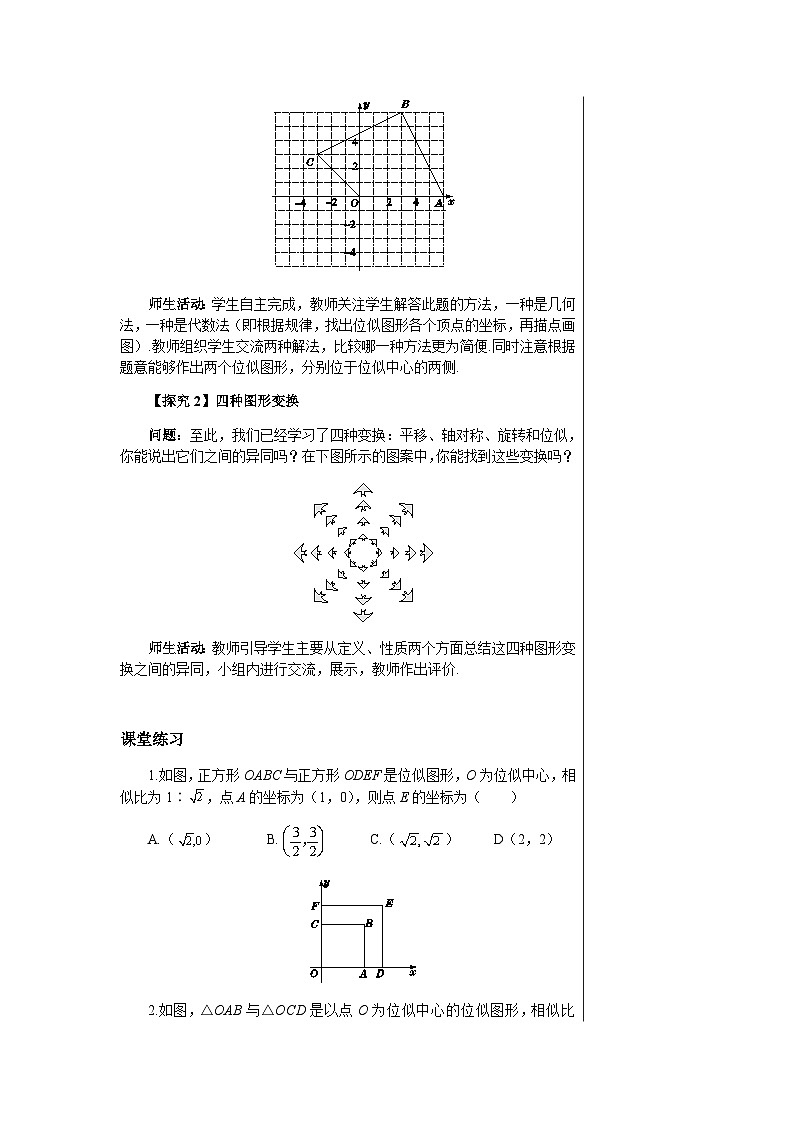
初中数学湘教版九年级上册3.6 位似一等奖教学ppt课件

这是一份初中数学湘教版九年级上册3.6 位似一等奖教学ppt课件，文件包含教学课件九上·湘教·36位似第2课时平面直角坐标系中的位似pptx、数学九上·湘教·36位似第2课时平面直角坐标系中的位似教案docx等2份课件配套教学资源，其中PPT共17页， 欢迎下载使用。

3.6.2 平面直角坐标系中的位似
湘教版数学九年级上册
能熟练在坐标系中根据坐标的变化规律做出位似图形，求某些特殊点的坐标.(难点)
1
2
掌握以坐标原点为位似中心的位似图形的变化规律. (重点)
学习目标
复习巩固
1. 两个相似多边形，如果它们对应顶点所在的直线相交于一点，我们就把这样的两个图形叫做 ，这个交点叫做 ．位似图形上任意一对对应 点到位似中心的距离之比等于 ， 对应线段 .
2. 如何判断两个图形是不是位似图形?
位似图形
位似中心
相似比 (或位似比)
平行或者在一条直线上
判断两个图形是不是位似图形，需要从两方面去考察：一是这两个图形是相似的，二是要有特殊的位置关系，即每组对应点所在的直线都经过同一点．
新课导入
3. 画位似图形的一般步骤有哪些？
（1）确定位似中心； （2）分别连接位似中心和能代表原图的关键点并延长； （3）根据相似比，确定能代表所画的位似图形的关键点； （4）按照原图的形状，顺次连接上述各点，得到放大或缩小后的图形.
我们知道，在直角坐标系中，可以利用变化前后两个多边形对应顶点的坐标之间的关系表示某些平移、轴对称和旋转 (中心对称). 那么，位似是否也可以用两个图形坐标之间的关系来表示呢？
如图，在平面直角坐标系中，已知△AOB的顶点坐标分别为A（2，4），O（0，0），B（6，0）.
知识讲解
由图可知，△A′OB′与△AOB是以坐标原点O为位似中心，位似比为2的位似图形.
数学上可以证明，一个多边形的顶点坐标分别扩大或缩小相同的倍数，所得到的图形与原图形是以坐标原点为位似中心的位似图形.
在平面直角坐标系中，如果以坐标原点为位似中心，位似比为k，那么位似图形对应点的坐标的比等于k.
例 如下图，在平面直角坐标系中，已知平行四边形OABC的顶点坐标分别为O（0，0），A（3，0），B（4，2）， C（1，2）. 以坐标原点O为位似中心，将平行四边形OABC放大为原图形的3倍.
分析 为了将平行四边形OABC放大为原图形的3倍，我们可以将原四边形每个顶点的横坐标、纵坐标都乘3，或都乘-3.
 
C
 
A
随堂训练
4.已知在平面直角坐标系中，点A(-3，-1)、B(-2，-4)、C(-6，-5)，以原点为位似中心将△ABC缩小，位似比为1:2，则点B的对应点的坐标为 ．
(-1，-2)、(1，2)
3.如图，已知△OAB与△OA′B′是相似比为1：2的位似图形，点O为位似中心，若△OAB内一点P（x，y）与△OA′B′内一点P′是一对对应点，则P′的坐标是　 　．
（﹣2x，﹣2y）
 
解：（1）如图所示．（2）如图所示．（3 )（ 2a , 2b ）或（ -2a ,-2 b ）.
点拨：以原点为位似中心的两个位似图形中，如果相似比为k，那么点（ a , b ）的对应点的坐标为（ k a , k b ）（位似图形在原点的同侧）或（- k a ,- k b ）（位似图形在原点的两侧）．
平面直角坐标系中的位似变换
在平面直角坐标系中，以原点为位似中心作一个图形的位似图形可以作两个．
当位似图形在原点同侧时，其对应顶点的坐标的比为 k；当位似图形在原点两侧时，其对应顶点的坐标的比为－k ．
当 k＞1 时，图形扩大为原来的 k 倍；当 0＜k＜1时，图形缩小为原来的 k 倍．
课堂小结