中考数学复习压轴解答题题组练二含答案

  压轴解答题题组练二

(针对中考：解答题第24—25题)

(时间：45分钟　　满分：20分)　　　　　　　　　　　　　　　

1．(10分)在平面直角坐标系中，抛物线y＝ax2＋bx＋4(a≠0)的图象经过点A(－2，0)，B(4，0)，与y轴交于点C，连接AC.

(1)求抛物线的函数解析式；

(2)如图①，连接BC，点P为第一象限抛物线上一动点，过点P作PM∥x轴交直线BC于点M，过点P作PN∥AC交x轴于点N，求PN＋PM的最大值及此时点 P的坐标；

(3)如图②，把抛物线y＝ax2＋bx＋4向右平移2个单位长度，平移后的抛物线与原抛物线相交于点Q，点E是原抛物线对称轴上一动点，点F是平移后抛物线上一动点，直接写出所有使得以点A，Q，E，F为顶点的四边形是平行四边形的点F的坐标，并把求其中一个点F的坐标的过程写出来．

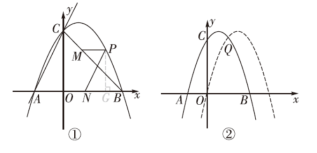
解：(1)抛物线的函数解析式为y＝－x2＋x＋4.

(2)设P(0＜t＜4)，

过点P作PG⊥x轴于点G，则

∠PGN＝90°，PG＝－t2＋t＋4，

∵抛物线y＝－x2＋x＋4与y轴交于点C，

∴C(0，4)，∴OC＝4.

∵OA＝2，∴AC＝ ＝ ＝2 .

∵PN∥AC，∴∠PNG＝∠CAO.

∵∠PGN＝∠COA＝90°，∴△PNG∽△CAO，

∴＝＝＝，∴PG＝PN.

∵B(4，0)，C(0，4)，

∴直线BC的解析式为y＝－x＋4.

∵PM∥x轴，∴点M的纵坐标为－t2＋t＋4，

∴－x＋4＝－t2＋t＋4，解得x＝t2－t，

∴M，

∴PM＝t－＝－t2＋2t，

∴PN＋PM＝PG＋PM

  ＝－t2＋t＋4＋

  ＝－＋.

∵－1＜0，0＜t＜4，∴当t＝时，PN＋PM有最大值，最大值为，此时点P的坐标为.

(3)抛物线y＝－x2＋x＋4向右平移2个单位长度，得到新抛物线y＝－x2＋3x，联立两函数解析式，得解得∴Q(2，4)．

∵原抛物线的对称轴为直线x＝1，∴设E(1，m)．

∵点F是平移后抛物线上一动点，

∴设F.

Ⅰ)当AQ，EF为对角线时，AQ，EF的中点重合，

∴n＋1＝2－2，解得n＝－1，

∴－n2＋3n＝－，∴F；

Ⅱ)当AE，FQ为对角线时，AE，FQ的中点重合，

∴n＋2＝－2＋1，解得n＝－3，

∴－n2＋3n＝－，∴F；

Ⅲ)当AF，EQ为对角线时，AF，EQ的中点重合，

∴n－2＝1＋2，解得n＝5，

∴－n2＋3n＝，∴F；

综上所述，点F的坐标为，或.

2．(10分)在△ABC中，∠BAC＝90°，AB＝AC＝2，D为BC的中点，E，F分别为AC，AD上任意一点，连接EF，将线段EF绕点E顺时针旋转90°得到线段EG，连接FG，AG.

 　           ①　　　　　　　②              ③

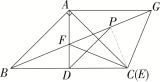
(1)如图①，点E与点C重合，且GF的延长线过点B，若点P为FG的中点，连接PD，求PD的长；

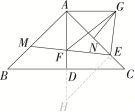
(2)如图②，EF的延长线交AB于点M，点N在AC上，∠AGN＝∠AEG且GN＝MF，求证：AM＋AF＝AE；

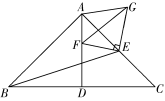
(3)如图③，F为线段AD上一动点，E为AC的中点，连接BE，H为直线BC上一动点，连接EH，将△BEH沿EH翻折至△ABC所在平面内，得到△B′EH，连接B′G，直接写出线段B′G的长度的最小值．

(1)解：如图①，连接CP，

由旋转知CF＝CG，∠FCG＝90°，

∴△FCG为等腰直角三角形，

∵点P是FG的中点，∴CP⊥FG，

∵点D是BC的中点，∴DP＝BC，

在Rt△ABC中，AB＝AC＝2，

∴BC＝AB＝4，∴DP＝2.

(2)证明：如图②，过点E作EH⊥AE交AD的延长线于点H，∴∠AEH＝90°，

由旋转知EG＝EF，∠FEG＝90°，

∴∠FEG＝∠AEH，∴∠AEG＝∠HEF，

∵AB＝AC，点D是BC的中点，

∴∠BAD＝∠CAD＝∠BAC＝45°，

∴∠H＝90°－∠CAD＝45°＝∠CAD，

∴AE＝HE，∴△EGA≌△EFH(SAS)，

∴AG＝HF，∠EAG＝∠H＝45°，

∵∠AGN＝∠AEG，∴∠AGN＝∠HEF，

∴∠AGN＝∠AMF，

∵GN＝MF，∴△AGN≌△AMF(AAS)，

∴AG＝AM，∵AG＝FH，∴AM＝FH，

∴AF＋AM＝AF＋FH＝AH＝AE.

(3)解：∵点E是AC的中点，

∴AE＝AC＝，

根据勾股定理得BE＝＝，

由折叠知BE＝B′E＝，

∴点B′是在以点E为圆心，为半径的圆上，

由旋转知EF＝EG，

∴点G是在以点E为圆心，EG为半径的圆上，

∴B′G的最小值为B′E－EG，

要使B′G最小，则EG最大，即EF最大，

∵点F在AD上，

∴点F在点A或点D时，EF最大，最大值为，

∴线段B′G的长度的最小值为－.