

广东省清远市清新区2022-2023学年高二下学期6月月考数学试题(无答案)
展开![]() 2022-2023学年度第二学期高二级6月月考
2022-2023学年度第二学期高二级6月月考
数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.将5封信投入3个邮筒,不同的投法共有( )
A.![]() 种 B.
种 B.![]() 种 C.
种 C.![]() 种 D.
种 D.![]() 种
种
2.已知随机变量![]() 的分布列
的分布列![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,则实数
垂直,则实数![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.4 D.3
C.4 D.3
4.数轴上一个质点在随机外力的作用下,从原点0出发,每隔1秒向左或向右移动一个单位,已知向右移动的概率为![]() ,向左移动的概率为
,向左移动的概率为![]() ,共移动6次,则质点位于2的位置的概率是( )
,共移动6次,则质点位于2的位置的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.某人将斐波那契数列的前6项“![]() ”进行排列设置数字密码,其中两个“1”必须相邻,则可以设置的不同数字密码有( )
”进行排列设置数字密码,其中两个“1”必须相邻,则可以设置的不同数字密码有( )
A.120种 B.240种 C.360种 D.480种
6.云计算是信息技术发展的集中体现,近年来,我国云计算市场规模持续增长.已知某科技公司2018年至2022年云计算市场规模数据,且市场规模![]() 与年份代码
与年份代码![]() 的关系可以用模型
的关系可以用模型![]() (其中
(其中![]() 为自然对数的底数)拟合,设
为自然对数的底数)拟合,设![]() ,得到数据统计表如下:
,得到数据统计表如下:
年份 | 2018年 | 2019年 | 2020年 | 2021年 | 2022年 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
云计算市场规模 | 7.4 | 11 | 20 | 36.6 | 66.7 |
| 2 | 2.4 | 3 | 3.6 | 4 |
由上表可得经验回归方程![]() ,则2025年该科技公司云计算市场规模
,则2025年该科技公司云计算市场规模![]() 的估计值( )
的估计值( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.![]() 的展开式中,
的展开式中,![]() 的系数为( )
的系数为( )
A.60 B.![]() C.30 D.
C.30 D.![]()
8.某公司生产一种产品,固定成本为20000元,每生产一单位的产品,成本增加100元,若总收入![]() 元与年产量
元与年产量![]() 的关系是
的关系是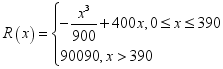 ,则当总利润最大时,每年生产产品的单位数是( )
,则当总利润最大时,每年生产产品的单位数是( )
A.150 B.200 C.250 D.300
二、多选题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.
9.在![]() 的展开式中,二项式的系数和为256,则下列说法正确的是( )
的展开式中,二项式的系数和为256,则下列说法正确的是( )
A.![]() B.展开式中各项系数和为256
B.展开式中各项系数和为256
C.第4项的二项式系数最大 D.展开式中所有系数的绝对值的和为4
10.给出以下四个说法,正确的有( )
A.如果由一组样本数据![]() 得到的经验回归方程是
得到的经验回归方程是![]() ,那么经验回归直线至少经过点
,那么经验回归直线至少经过点![]() 中的一个
中的一个
B.在残差的散点图中,残差分布的水平带状区域的宽度越窄,其模型的拟合效果越好
C.在回归分析中,用决定系数![]() 来比较两个模型拟合效果,
来比较两个模型拟合效果,![]() 越大,表示残差平方和越小,即模型的拟合效果越好
越大,表示残差平方和越小,即模型的拟合效果越好
D.设两个变量![]() 之间的线性相关系数为
之间的线性相关系数为![]() ,则
,则![]() 的充要条件是成对数据构成的点都在经验回归直线上
的充要条件是成对数据构成的点都在经验回归直线上
11.为了考察某种疫苗的预防效果,先选取某种动物进行实验,试验时得到如下统计数据:
| 未发病 | 发病 | 总计 | |||
未注射疫苗 |
|
|
| |||
注射疫苗 | 40 |
|
| |||
总计 | 70 |
| 100 | |||
| 0.1 | 0.05 | 0.01 | 0.005 | 0.001 | |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 | |
现从实验动物中任取一只,若该动物“注射疫苗”的概率为0.5,则下列判断正确的是( )
A.未注射疫苗发病的动物数为30只
B.从该实验注射疫苗的动物中任取一只,发病的概率为![]()
C.在犯错概率不超过0.05的前提下,认为未发病与注射疫苗有关
D.注射疫苗可使实验动物的发病率下降约![]()
12.已知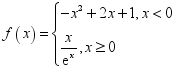 ,若关于
,若关于![]() 的方程
的方程![]() 恰好有6个不同的实数解,则
恰好有6个不同的实数解,则![]() 的取值可以是( )
的取值可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
三、填空题:本题共4小题,每小题5分,共20分.
13.某班将5名同学分配到甲、乙、丙三个社区参加劳动锻炼,每个社区至少分配一名同学,则甲社区恰好分配2名同学共有______种不同的方法(用数字作答).
14.某同学上学路上要经过3个路口,在每个路口遇到红灯的概率都是![]() ,且在各路口是否遇到红灯是相互独立的,记
,且在各路口是否遇到红灯是相互独立的,记![]() 为遇到红灯的次数,若
为遇到红灯的次数,若![]() ,则
,则![]() 的方差
的方差![]() ________.
________.
15.某杂交水稻种植研究所调查某地水稻的株高时,发现株高(单位:![]() )服从正态分布
)服从正态分布![]() ,若测量10000株水稻,株高在
,若测量10000株水稻,株高在![]() 的约有_______株.(若
的约有_______株.(若![]() ,
,![]() .
.
16.在临床上,经常用某种试验来诊断试验者是否患有某种癌症,设![]() “试验结果为阳性”,
“试验结果为阳性”,![]() “试验者患有此癌症”,据临床统计显示
“试验者患有此癌症”,据临床统计显示![]() .已知某地人群中患有此种癌症的概率为0.001,现从该人群中随机抽在了1人,其试验结果是阳性,则此人患有此种癌症的概率为_______.
.已知某地人群中患有此种癌症的概率为0.001,现从该人群中随机抽在了1人,其试验结果是阳性,则此人患有此种癌症的概率为_______.
四、解答题:本题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(10分)在![]() 中,内角
中,内角![]() 的对边分别为
的对边分别为![]() ,若
,若![]() .
.
(1)求角![]() 的大小;
的大小;
(2)若![]() .且
.且![]() ,求
,求![]() 的面积.
的面积.
18.(12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() 是公差为1的等差数列.
是公差为1的等差数列.
(1)求![]() 的通项公式;
的通项公式;
(2)记![]() ,求证:
,求证:![]() .
.
19.(12分)如图,在四棱雉![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上,且
上,且![]() 平面
平面![]() .
.
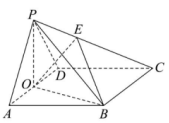
(1)求![]() 的值;
的值;
(2)若![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
20.(12分)血液检测是诊断是否患某疾病的重要依据,通过提取病人的血液样本进行检测,样本的某一指标会呈现阳性或阴性.若样本指标呈阳性,说明该样本携带病毒;若样本指标呈阴性,说明该样本不携带病毒.根据统计发现,每个疑似病例的样本呈阳性(即样本携带病毒)的概率均为![]() .现有4例疑似病例,分别对其进行血液样本检测.多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要携带病毒,则混合样本化验结果就会呈阳性.若混合样本呈阳性,则将该组中各个样本再逐个化验;若混合样本呈阴性,则该组各个样本均为阴性.现有以下两种方案:方案一:逐个化验;方案二:平均分成两组化验.在该疾病爆发初期,由于检测能力不足,化验次数的期望值越小,则方案越优”.
.现有4例疑似病例,分别对其进行血液样本检测.多个样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要携带病毒,则混合样本化验结果就会呈阳性.若混合样本呈阳性,则将该组中各个样本再逐个化验;若混合样本呈阴性,则该组各个样本均为阴性.现有以下两种方案:方案一:逐个化验;方案二:平均分成两组化验.在该疾病爆发初期,由于检测能力不足,化验次数的期望值越小,则方案越优”.
(1)若![]() ,求这4例疑似病例中呈阳性的病例个数
,求这4例疑似病例中呈阳性的病例个数![]() 的分布列;
的分布列;
(2)若将该4例疑似病例样本进行化验,且方案二比方案一更“优”,求![]() 的取值范围.
的取值范围.
21.(12分)椭圆![]() 的离心率为
的离心率为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆上运动,且
在椭圆上运动,且![]() 的最大值为
的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作斜率分别为
作斜率分别为![]() 的两条直线分别交椭圆于点
的两条直线分别交椭圆于点![]() ,且
,且![]() ,证明:直线
,证明:直线![]() 恒过定点.
恒过定点.
22.(12分)已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
2022-2023学年广东省清远市”四校联盟”高一下学期期中数学试题含答案: 这是一份2022-2023学年广东省清远市”四校联盟”高一下学期期中数学试题含答案,共12页。试卷主要包含了单选题,多选题,填空题,双空题,解答题等内容,欢迎下载使用。
2022-2023学年广东省清远市清新区第一中学高二下学期5月月考数学试题含答案: 这是一份2022-2023学年广东省清远市清新区第一中学高二下学期5月月考数学试题含答案,共17页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年广东省清远市高二下学期期末数学试题含答案: 这是一份2022-2023学年广东省清远市高二下学期期末数学试题含答案,共15页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。












