25章 图形的相似复习课（教学设计）-2023-2024学年冀教版九年级上学期数学

第二十五章 图形的相似

【教材分析】本节课是冀教版九年级上册第25章的内容，相似三角形是在全等三角形知识的基础上拓广和发展的，它在工农业生产、土木建筑、测量绘图和日常生活中有着广泛的应用。本课主要是复习相似三角形的判定和性质及其应用。

【学情分析】本节课是一节复习课，学生已经学过相似三角形的有关知识，本节课将通过关注相似图形的变式，帮助学生自主构建知识网络，将相似三角形的定义，判定，性质，应用等知识形成知识网络，还应与全等形等知识联网。通过本节课的学习，培养学生猜想、实验、证明、探索等能力，对掌握观察、比较、类比、转化等思想有重要作用。

【教学目标】1.疏通本章知识，弄清知识脉络，体会知识间的内在联系；

2.进一步熟悉相似三角形的判定及其性质，并能运用这些判定和性质解决一些相应的问题。

3.养成合作交流与总结的习惯，培养学生推理能力和空间想象能力.

【教学重难点】熟悉相似三角形的基本构图，综合运用相似三角形的判定定理及性质定理解决问题。

【教      具】多媒体、课件

【教学过程】

一、回顾提升

1.比例的基本性质是什么？

2.如何判断四条线段成比例？

3.什么是线段的黄金分割点？黄金比值是多少？

4.由平行线推出成比例线段的比例时，要注意什么？

5.相似三角形定义：_________________________．

6.判定方法：__________________________.

7.相似三角形性质：

（1）对应角相等，对应边成比例；（2）对应线段之比等于           ；（对应线段包括哪几种主要线段？）（3）周长之比等于            ；（4）面积之比等于          ．

8.位似形的性质：          . 

9.将一个图形按一定的比例放大或缩小的步骤为：           .

10.相似三角形中的基本图形:（1）平行型（X型，A型）：                              

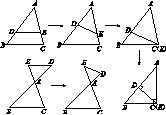
（2）交错型；（3）旋转型；（4）母子三角形.       

二、综合应用

知识1  比例的基本性质

1. 已知＝(a，b，c，d均不为0)，则下列等式中不成立的是(　　)

A.＝       B.＝       C.＝        D.＝

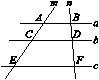
2.如图，已知直线a∥b∥c，直线m，n与a，b，c分别交于

点A，C，E，B，D，F.若AC＝4，CE＝6，BD＝3，

则DF的值是(　　)

A．4　　　　B．4.5      C．5        D．5.5

3.如图所示，点C 把线段AB分成两条线段AC、BC，且AC＞BC，下列说法错误的是(　　)

A．如果,那么线段AB 被点C 黄金分割

B．如果 ＝AB·BC，那么线段AB 被点C 黄金分割

C．如果线段AB被点C黄金分割，则线段AC 与AB 的比叫做黄金比

D．如果线段AB被点C黄金分割，则 ＝0.618

知识2  相似三角形

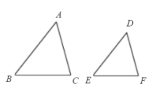1.如图，(1)已知,要使∆ABC∽∆DEF，

还需添加一个条件，你添加的条件是        .  

(2)已知，要使∆ABC∽∆DEF，

还需添加一个条件，你添加的条件是         .

2.已知∆ABC∽∆DEF，

(1)你能得到哪些结论?

(2）若AM、DN分别是BC、EF边上的中线，AB=6，AM=4，DE=5，DN=          .

3.已知两个相似三角形的面积比等于4:9，则它们的周长比是            .

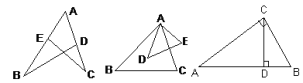
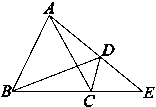4.如图，在四边形ABCD中，∠ADB＝∠ACB，延长AD，BC相交于点E.

求证：(1)△ACE∽△BDE；

(2)BE·DC＝AB·DE.

知识3 相似三角形的应用

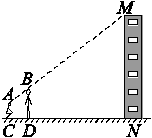
 亮亮和颖颖住在同一幢住宅楼，两人准备用测量影子的方法测算其楼高，但恰逢阴天，于是两人商定改用下面方法：如图，亮亮蹲在地上，颖颖站在亮亮和楼之间，两人适当调整自己的位置，当楼的顶部M，颖颖的头顶B及亮亮的眼睛A恰在一条直线上时，

两人分别标定自己的位置C，D，然后测出两人之间的距离CD＝1.25 m，

颖颖与楼之间的距离DN＝30 m(点C，D，N在一条直线上)，

颖颖的身高BD＝1.6 m，亮亮蹲地观测时眼睛到地面的距离AC＝0.8 m.

请你根据以上测量数据帮助他们求出这幢住宅楼的高度．

师生活动：教师提出问题；学生积极的思考、讨论整理出解决本题的思路．教师应注意学生对相似三角形判定的思路，方法，及时地鼓励和点评并最后总结本题的答案．

知识4　位似图形

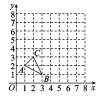如图，△ABC三个顶点的坐标分别为A(1，2)，B(3，1)，C(2，3)，以原点O为位似中心，将△ABC放大为原来的2倍得到△A′B′C′.

(1)在图中第一象限内画出符合要求的△A′B′C′(不要求写画法)；

(2)△A′B′C′的面积是________．

三、课堂小结

【作业设计】

基础性作业【必做】“找”“选”相似基本型解题。

如图，已知△ABC、△DCE、△FEG是三个全等的等腰三角形，底边BC，CE，EG在同一直线上，

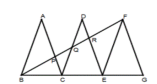且 AB=，BC=1，BF分别交AC、DC，DE于点P、Q、R.

求证:（1)△BFG∽△FEG;

(2）求AP: PC.

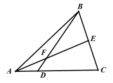拓展性作业【选做】“造”相似基本型解题，而且该题至少有10种不同的解题方法。

如图，在△ABC中，AD:DC=1:2，BE:EC=3:2，求DF:BF.

(找尽可能多的方法哦! )