北京市顺义区2022-2023学年八年级下学期数学期末试题（含答案）

顺义区2022-2023学年度第二学期八年级教学质量检测

数学试卷

考生须知

1．本试卷共8页，共三道大题，28道题，满分100分。考试时间120分钟。

2．在答题卡上准确填写学校、班级、姓名和准考证号。

3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4．在答题卡上，选择题、作图题用2B铅笔作答，其他试题用黑色字迹签字笔作答。

5．考试结束，将答题卡交回。

一、选择题（本题共16分，每题2分）

第1-8题均有四个选项，符合题意的选项只有一个

1．在平面直角坐标系中，点关于轴的对称点的坐标是（    ）

A． B． C． D．

2．下列几何体中，是圆柱体的为（    ）

A． B． C． D．

3．若一个多边形的内角和与外角和相等，则这个多边形是（    ）

A．三角形 B．四边形 C．五边形 D．六边形

4．方程的解为（    ）

A． B． C． D．

5．如图，在平行四边形中，对角线相交于点．则图中全等三角形的对数是（    ）

A．2对 B．3对 C．4对 D．5对

6．如图，顺次连接矩形各边中点，得到由矩形和菱形组成的图形，则关于这个图形的描述正确的是（    ）

A．是轴对称图形但不是中心对称图形 B．不是轴对称图形也不是中心对称图形

C．不是轴对称图形但是中心对称图形 D．是轴对称图形也是中心对称图形

7．用配方法解一元二次方程，则此方程可化为（    ）

A． B． C． D．

8．下面的三个问题中都有两个变量：

①正方形的面积与边长

②将水箱中的水匀速放出，直至放完，水箱中剩余水量与放水时间

③汽车从A地匀速行驶到地，汽车距离地的路程与行驶时间

其中，变量与变量之间的函数关系可以利用如图所示的图象表示的是（    ）

A．①② B．①③ C．②③ D．①②③

二、填空题（本题共16分，每题2分）

9．的相反数是_________．

10．方程的解为_________．

11．如图，在中，为边的中点，则_________．

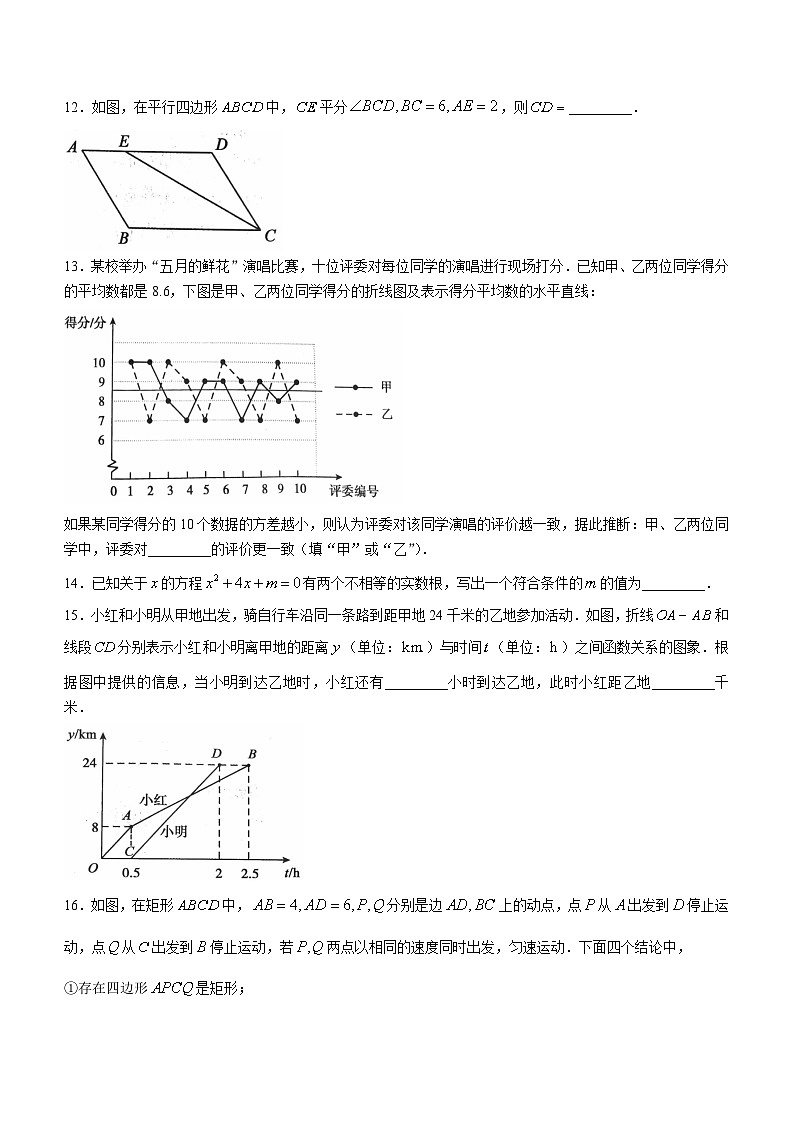
12．如图，在平行四边形中，平分，则_________．

13．某校举办“五月的鲜花”演唱比赛，十位评委对每位同学的演唱进行现场打分．已知甲、乙两位同学得分的平均数都是8.6，下图是甲、乙两位同学得分的折线图及表示得分平均数的水平直线：

如果某同学得分的10个数据的方差越小，则认为评委对该同学演唱的评价越一致，据此推断：甲、乙两位同学中，评委对_________的评价更一致（填“甲”或“乙”）．

14．已知关于的方程有两个不相等的实数根，写出一个符合条件的的值为_________．

15．小红和小明从甲地出发，骑自行车沿同一条路到距甲地24千米的乙地参加活动．如图，折线和线段分别表示小红和小明离甲地的距离（单位：）与时间（单位：）之间函数关系的图象．根据图中提供的信息，当小明到达乙地时，小红还有_________小时到达乙地，此时小红距乙地_________千米．

16．如图，在矩形中，分别是边上的动点，点从出发到停止运动，点从出发到停止运动，若两点以相同的速度同时出发，匀速运动．下面四个结论中，

①存在四边形是矩形；

②存在四边形是菱形；

③存在四边形是矩形；

④存在四边形是正方形．

所有正确结论的序号是_________．

三、解答题（本题共68分，第17-19题，每题5分，第20-22题，每题6分，第23题5分，第24，25题，每题6分，第26题5分，第27题7分，第28题6分）

解答应写出文字说明、演算步骤或证明过程

17．解不等式组：

18．解方程：．

19．下表是一次函数中与的两组对应值．

（1）求该一次函数的表达式；

（2）求该一次函数的图象与轴的交点坐标．

20．下面是小红设计的“已知直角作矩形”的尺规作图过程．

已知：如图，．

求作：矩形．

作法：如图，

①在的两边上分别任取点（不与点重合）；

②以点为圆心，长为半径画弧，以点为圆心，长为半径画弧，两弧在的内部交于点；

③连接．

所以四边形即为所求作的矩形．

根据小红设计的尺规作图过程

（1）使用直尺和圆规，补全图形（保留作图痕迹）；

（2）完成下列证明．

证明：

∵_________，

∴四边形是平行四边形（_________）（填推理的依据）．

又∵，

∴四边形是矩形（_________）（填推理的依据）．

21．已知关于的一元二次方程．

（1）求证：方程总有两个不相等的实数根；

（2）若方程的一个根是1，求的值及方程的另一个根．

22．如图，在中，分别是的中点，．

（1）求证：四边形是菱形；

（2）连接，若，求的长．

23．某校打算用的篱笆，在墙边（墙足够长）围成一个矩形区域，作为“养殖基地”（篱笆只围三边），当矩形区域的面积是时，求它的长和宽．

24．在平面直角坐标系中，直线与轴交于点，直线与轴交于点，与交于点．

（1）求的面积；

（2）若的面积是面积的2倍，求的值．

25．2023年5月30日，神舟十六号载人飞船发射取得圆满成功．为普及航天知识，某中学举办了一次”航天知识竞赛”，共有1000名学生参加。为更好的了解本次比赛得分的分布情况，随机抽取了部分学生的比赛得分，进行收集、整理、描述和分析．下面给出了部分信息（数据分成5组：，，，，）：

a．学生比赛得分频数分布表：

c．学生比赛得分在这一组的是：

80  81  83  82  86  87  85  81  89  88  85  86  80  83

根据以上信息，回答下列问题：

（1）_________，_________；

（2）请补全频数分布直方图；

（3）若得分在85分及以上均为“优秀”，请估计参加这次比赛的1000名学生中得分优秀的人数．

26．在平面直角坐标系中，一次函数的图象经过点．

（1）求的值；

（2）当时，对于的每一个值，一次函数的值小于一次函数的值，直接写出b的取值范围．

27．如图，在正方形中，是边上的一动点（不与点重合），于点，，连接．

（1）求证：；

（2）延长，交于点，连接．

①依题意补全图形；

②用等式表示线段之间的数量关系，并证明．

28．在平面直角坐标系中，给出如下定义：若在图形上存在一点，且点的纵坐标是横坐标的（为正整数）倍，则称点为图形的“倍点”．

例如，点是直线的“4倍点”．

（1）在点中，_________是直线的“2倍点”；

（2）已知点的坐标为，点的坐标为，以线段为矩形的一边向上作矩形．

①若，判断是否存在矩形的“3倍点”，若存在，求出矩形的“3倍点”的坐标，若不存在，请说明理由；

②若，且存在矩形的“倍点”，直接写出的取值范围．

顺义区2022-2023学年度第二学期期末八年级数学答案

一、选择题

二、填空题

9．2  10．  11．40  12．4  13．甲  14．0  15．0.5，4  16．①②③

三、解答题

17．解不等式组：

解不等式①得，

解不等式②得，

∴原不等式组的解集为．

18．解：

19．解：

（1）依题意得：解得

∴一次函数表达式．

（2）令，则，

∴

∴一次函数的图象与x轴的交点坐标为．

20．解：（1）

（2）：

两组对边分别相等的四边形是平行四边形

有一个角是直角的平行四边形是矩形

21．解：（1）依题可得

∵，∴

即

∴关于的一元二次方程有两个不相等的实数根．

（2）当．

∴，

∴方程为，∴．

22．（1）

证明：∵，

∴四边形是平行四边形．

又∵在中，，分别是的中点，

∴，

又∵，

∴，

∴四边形是菱形．

（2）解：∵，

∴，∴，

又∵，

∴在中，．

∴．

23．解：设矩形长为米，则宽为米．

依题意可列方程

答：矩形的长、宽分别为，或、米．

24．（1）令，则，∴点坐标为

令，则，∴点坐标为

∴，

∴．

（2）由题意得：

∵

∴，∴，

当时，，∴点丛标为；

当时，，∴点坐标为；

∴约值为1或．

25．解：（1）0.28，50

（2）

（3）（人）

这次比基的1000名等生中得分优祭的人数大约是340人．

26．解：

（1）把点坐标代入一次函数

则，．

（2）

27．（1）证明：

∵边形是正方形，

∴．

∵于点，

∴，∴，

又∵，

∴，

∴．

（2）①

②线段之间的数量关系是

延长到点，使，连接．

∵，

∴，∴．

又∵，

∴，

∴．

∵，∴．

即．

∴是等腰直角三角形．

∴，

∴，∴．

28．（1）．

（2）

①时，点些标为，点坐被为

三倍点在直线上，

当时，，点；

当时，，点；

∴

②．