初中数学中考复习：15二次函数(含答案)

中考总复习：二次函数—巩固练习（基础）

【巩固练习】

一、选择题

1．二次函数的图象的顶点坐标是(    )  

    A．(-1，8)    B．(1，8)    C．(-1，2)    D．(1，-4)

2．若，三点都在函数的图象上，则的大小关系是(   )
　　A. 　　　B. 　　　 C. 　　　D.

3．函数在同一直角坐标系内的图象大致是(    )

4.如图是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A（－3，0），

对称轴为x＝－1．给出四个结论：①b2＞4ac；②2a＋b=0；③a－b＋c=0；

④5a＜b．其中正确结论是（　　）．

A．②④  B. ①④  C. ②③  D. ①③

5.抛物线y=ax2+bx+c图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（   ）

;

6.矩形ABCD中，．动点E从点C开始沿边CB向点以2cm/s的速度运动至点B停止，动点F从点C同时出发沿边CD向点D以1cm/s的速度运动至点D停止．如图可得到矩形CFHE，设运动时间为x（单位：s），此时矩形ABCD去掉矩形CFHE后剩余部分的面积为y(单位：)，则y与x之间的函数关系用图象表示大致是下图中的（    ）

二、填空题

7．如图所示的抛物线是二次函数的图象，那么的值是          ．

8．二次函数y =ax2＋bx＋c 的图象如图所示，且P=| a－b＋c |＋| 2a＋b |，Q=| a＋b＋c |＋| 2a－b |，

则P、Q的大小关系为               .

9．给出下列命题：

命题1．点(1，1)是双曲线与抛物线的一个交点．

命题2．点(1，2)是双曲线与抛物线的一个交 点．

命题3．点(1，3)是双曲线与抛物线的一个交点．

……

请你观察上面的命题,猜想出命题(是正整数):                          .

10．抛物线y=ax2与直线x=1，x=2，y=1，y=2组成的正方形有公共点，则a的取值范围是           .

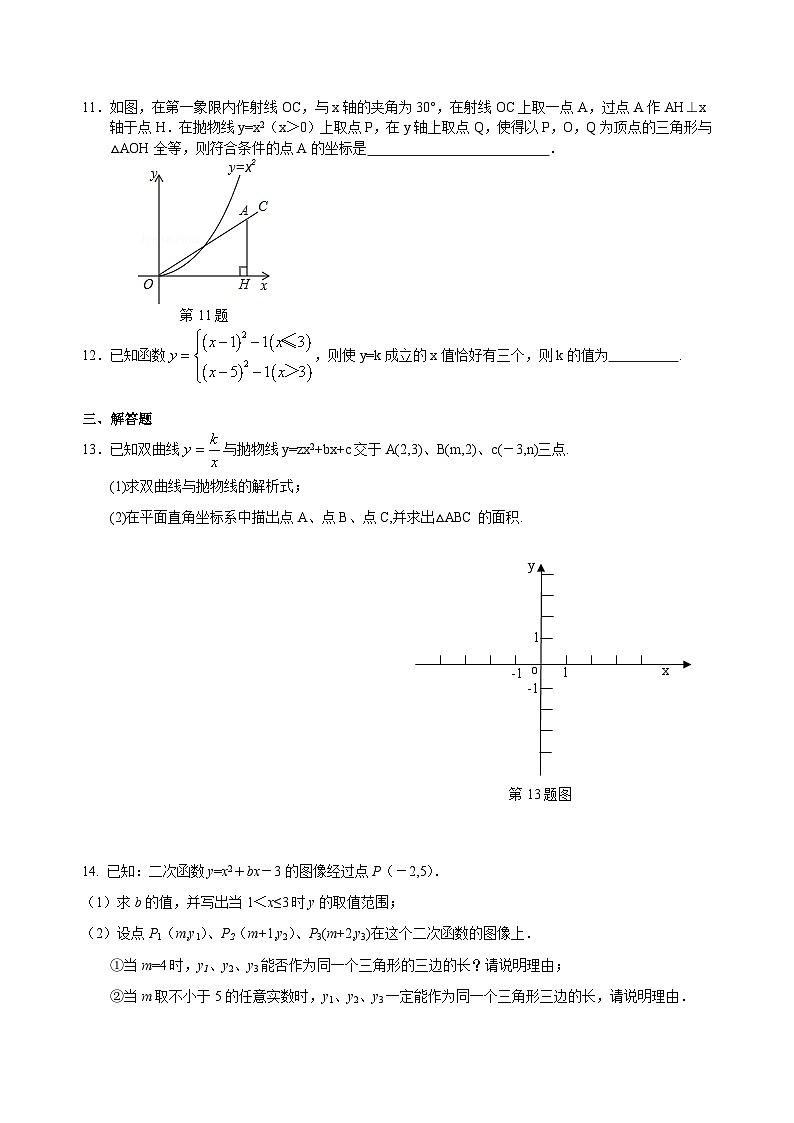
11．如图，在第一象限内作射线OC，与x轴的夹角为30°，在射线OC上取一点A，过点A作AH⊥x轴于点H．在抛物线y=x2（x＞0）上取点P，在y轴上取点Q，使得以P，O，Q为顶点的三角形与△AOH全等，则符合条件的点A的坐标是　                      　．

第11题                                   

12．已知函数，则使y=k成立的x值恰好有三个，则k的值为          .

三、解答题

13．已知双曲线与抛物线y=zx2+bx+c交于A(2,3)、B(m,2)、c(－3,n)三点.

    (1)求双曲线与抛物线的解析式；

    (2)在平面直角坐标系中描出点A、点B、点C,并求出△ABC的面积.

14. 已知：二次函数y=x2＋bx－3的图像经过点P（－2,5）．

（1）求b的值，并写出当1＜x≤3时y的取值范围；

（2）设点P1（m,y1）、P2（m+1,y2）、P3(m+2,y3)在这个二次函数的图像上．

①当m=4时，y1、y2、y3能否作为同一个三角形的三边的长？请说明理由；

②当m取不小于5的任意实数时，y1、y2、y3一定能作为同一个三角形三边的长，请说明理由．

15．关于x的方程

（1）当a取何值时，二次函数的对称轴是x=-2；

（2）求证：a取任何实数时，方程总有实数根.

16. 如图，开口向上的抛物线与轴交于A（，0）和B（，0）两点，和是方程的两个根（），而且抛物线交轴于点C，∠ACB不小于90°.

（1）求点A、点B的坐标和抛物线的对称轴；

（2）求系数的取值范围；

（3）在的取值范围内，当取到最小值时，抛物线上有点P，使，求所有满足条件的点P的坐标.

【答案与解析】

一、选择题

1.【答案】A；

【解析】求抛物线的顶点坐标有两种方法：①抛物线的顶点坐标为，将中的a，b，c直接代入即可求出；②采用配方法，即将变形为，所以的顶点坐标

为(-l，8)．

2.【答案】A；

【解析】主要考查反比例函数的图象和性质.解答时，应先画出的图象，如图，然后把 三点在图中表示出来，依据数轴的特性，易知，

故应选A.
                                 

3.【答案】C；

【解析】当>0时，抛物线开口向上，一次函数图象过一、三象限，所以排除A选项，再看B、C选项，抛物线对称轴在y轴右侧，a、b异号，所以一次函数应与y轴交于负半轴，排除B选项；当<0时，抛物线开口向下，而一次函数图象过二、四象限，排除D选项.所以答案选C.

4.【答案】B； 

5.【答案】D；

【解析】从二次函数图像可看出>0，>0,得b0,c0,b2-4c>0.又可看出当x=1时，y0.

      所以0，由此可知D答案正确.

6.【答案】A；

【解析】分段函数y1=-2x2+48 (0≤x<4)； y2=-8x+48 (4≤x<6),故选A.

二、填空题

7．【答案】－1；

  【解析】图象经过原点（0,0），把点（0,0）代入得，因为抛物线开口向下，所以.

8．【答案】P<Q ；

【解析】由抛物线的图象可以知道：

（1）开口向下， a＜0；（2）抛物线过原点，c=0 ；

（3）对称轴x=﹣＞1，则b＞﹣2a，即b+2a＞0；

（4）当x=﹣1时，y =ax2＋bx＋c= a－b+ c＜0；

（5）当x=1时，y =ax2＋bx＋c= a+b+ c＞0；

（6）因为a＜0，b＞﹣2a，所以，b＞0，因此，2a－b＜0；

则：P－Q=[﹣（a－b+c）+(2a+b)]－[(a+b+c)－(2a－b)]

              =﹣a+b－c+2a+b－a－b－c+2a－b

              =2a＜0

所以，P＜Q

9．【答案】点(1，n)是双曲线与抛物线的一个交点 ．

10．【答案】

【解析】如图，四条直线x=1，x=2，y=1，y=2围成正方形ABCD，

因为抛物线与正方形有公共点，所以可得a＞0，而且a值越大，抛物线开口越小，

因此当抛物线分别过A（1，2），C（2，1）时，

a分别取得最大值与最小值，代入计算得出：a=2，a=；

由此得出a的取值范围是．

11．【答案】（3，）、（，）、（2，2）、（，）．

   【解析】由题可得A的纵坐标是横坐标的倍，故设A的坐标为（t，t）；

则Q的坐标为（0，2t）或（0，t）；

可求得P点对应的坐标，解得t的值有4个，为，，2，；

故点A的坐标是（3，）、（，）、（2，2）、（，）．

12．【答案】3；

【解析】函数的图象如图：

，

根据图象知道当y=3时，对应成立的x有恰好有三个，∴k=3．

三、解答题

13.【答案与解析】

 (1)把点A(2,3)代入得  ：k=6.

 ∴反比例函数的解析式为：.

 把点B(m,2)、C(－3,n)分别代入得： m=3,n=-2.

 把A(2,3)、B(3,2)、C(-3,-2)分别代入y=ax2+bx+c得：

  解之得 

∴抛物线的解析式为：y=-.

(2)描点画图

S△ABC=(1+6)×5-×1×1-×6×4==5.

14.【答案与解析】

解：（1）把点P代入二次函数解析式得5= （－2）2－2b－3，解得b=－2.

当1＜x≤3时y的取值范围为－4＜y≤0.

（2）①m=4时，y1、y2、y3的值分别为5、12、21，由于5+12＜21，不能成为三角形的三边长．

②当m取不小于5的任意实数时，y1、y2、y3的值分别为m2－2m－3、m2－4、m2＋2m－3，由于，

m2－2m－3＋m2－4＞m2＋2m－3，（m－2）2－8＞0，

当m不小于5时成立，即y1＋y2＞y3成立．

所以当m取不小于5的任意实数时，y1、y2、y3一定能作为同一个三角形三边的长，

15.【答案与解析】

(1)解：∵二次函数的对称轴是x=-2

∴    

解得a=-1

经检验a=-1是原分式方程的解.

所以a=-1时，二次函数的对称轴是x=-2；

（2）①当a=0时，原方程变为-x-1=0，方程的解为x= -1；

    ②当a≠0时，原方程为一元二次方程，，

当方程总有实数根，

∴

整理得，

∵a≠0时，  总成立

所以a取任何实数时，方程总有实数根.

16.【答案与解析】

（1）A（－3，0）B（1，0），对称轴；

（2）    化简得    OC＝.

若∠ACB＝90°，则，，；

若∠ACB＞90°，则，；所以.

（3）由（2）有，当在取值范围内，取到最小值时，，，由AB＝，得：.

当时，，，∴（，），（，）；

当时，，，      ∴（0，），（－2，）.