2024全国一轮数学（基础版）第46讲 第2课时 非线性回归模型与曲线拟合课件PPT

这是一份2024全国一轮数学（基础版）第46讲 第2课时 非线性回归模型与曲线拟合课件PPT，共28页。PPT课件主要包含了研题型·融会贯通，举题说法，随堂内化等内容，欢迎下载使用。
例1　2021年6月，公安部推出国家级反诈防骗“王炸”系统——“国家反诈中心App”，这是一款能有效预防诈骗、快速举报诈骗内容的软件，用户通过学习里面的防诈骗知识可以有效避免各种网络诈骗的发生，减少不必要的财产损失，某省自“国家反诈中心App”推出后，持续采取多措并举的推广方式，积极推动全省“国家反诈中心App”安装注册工作．经统计，省反诈中心发现全省网络诈骗举报件数y(单位：件)与推广时间有关，并记录了经推广x个月后举报件数的数据如下表.
(2) 分析该省一直加大力度推广下去，有可能将网络诈骗举报件数降至接近于零吗？
y＝bxm＋a型的处理方法：设x′＝xm，原方程可化为y＝bx′＋a，再根据线性回归模型的方法求出a，b.
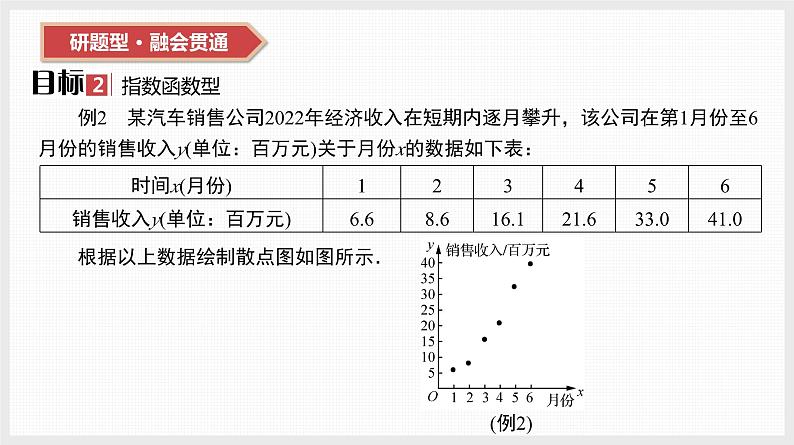
例2　某汽车销售公司2022年经济收入在短期内逐月攀升，该公司在第1月份至6月份的销售收入y(单位：百万元)关于月份x的数据如下表：
根据以上数据绘制散点图如图所示．
【解答】 y＝cedx，因为散点图中点的分布不是一条直线，相邻两点在y轴上差距是增大的趋势，故用y＝cedx表示更合适．
(1) 根据散点图判断，y＝ax＋b与y＝cedx(a，b，c，d均为常数)哪一个适宜作为该公司销售收入y关于月份x的回归方程类型？
(2) 根据(1)的结果及表中数据，求出y关于x的回归方程，并预测该公司8月份的销售收入．(结果近似到小数点后第二位)参考数据：
【解答】 由y＝cedx，得lny＝ln(cedx)＝lnc＋dx，设u＝lny，所以u＝lnc＋dx. 预测该公司8月份的销售收入为y＝e1.52＋0.38×8＝e4.56≈95.58(百万元)．
指数函数型y＝ebx＋a的处理方法：两边取对数得lny＝lnebx＋a，即lny＝bx＋a.令z＝lny，把原始数据(x，y)转化为(x，z)，再根据线性回归模型的方法求出a，b.
例3　“不关注分数，就是对学生的今天不负责；只关注分数，就是对学生的未来不负责．”为锻炼学生的综合实践能力，长沙市某中学组织学生对雨花区一家奶茶店的营业情况进行调查统计，得到的数据如下表.
(2) 从相关系数的角度确定哪一个模型的拟合效果更好，并据此预测次年2月(计x＝14)的净利润(保留1位小数)．
对数函数型y＝blnx＋a的处理方法：设x′＝lnx，原方程可化为y＝bx′＋a，再根据线性回归模型的方法求出a，b.
1. 用模型y＝cekx拟合一组数据时，为了求出经验回归方程，设z＝ln y，其变换后得到的经验回归方程为z＝0.5x＋2，则c等于(　 　)A. 0.5 B. e0.5 C. 2 D. e2
点击对应数字即可跳转到对应题目
【解析】 因为y＝cekx，两边取对数得lny＝ln(cekx)＝ln c＋ln ekx＝kx＋ln c，则z＝kx＋ln c，而z＝0.5x＋2，于是得ln c＝2，即c＝e2.
2. 已知变量x，y的关系可以用模型y＝c·ekx拟合，设z＝lny，其变换后得到一组数据如下表：
由y＝c·ekx，得z＝lny＝ln(cekx)＝lnc＋lnekx＝lnc＋kx，所以lnc＝－0.9，即c＝ e－0.9.
4. 已知变量y关于x的回归方程为y＝ebx－0.5，若对y＝ebx－0.5两边取自然对数，可以发现lny与x线性相关，现有一组数据如下表所示，当x＝5时，预测y的值为_________.
【解析】 对y＝ebx－0.5两边取对数，得lny＝bx－0.5，令z＝lny，则z＝bx－0.5，列表如下：