2024年新高考数学第一轮复习课件：第46讲　第2课时　非线性回归模型与曲线拟合

这是一份2024年新高考数学第一轮复习课件：第46讲　第2课时　非线性回归模型与曲线拟合，共23页。PPT课件主要包含了答案BC，e－2等内容，欢迎下载使用。
　　　 　由y＝menx，得z＝lny＝ln(menx)＝lnm＋nx＝0.3x－ln2，所以m＝0.5，n＝0.3.
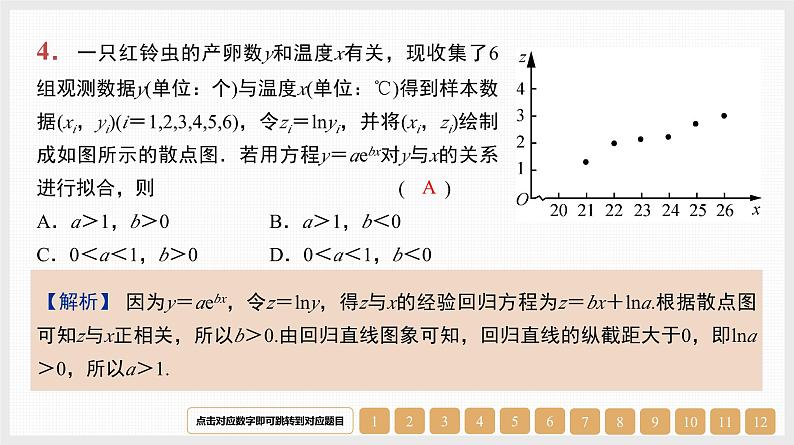
4．一只红铃虫的产卵数y和温度x有关，现收集了6组观测数据y(单位：个)与温度x(单位：℃)得到样本数据(xi，yi)(i＝1,2,3,4,5,6)，令zi＝lnyi，并将(xi，zi)绘制成如图所示的散点图．若用方程y＝aebx对y与x的关系进行拟合，则(　　)A．a＞1，b＞0　　B．a＞1，b＜0C．0＜a＜1，b＞0　　D．0＜a＜1，b＜0
　　　 　因为y＝aebx，令z＝lny，得z与x的经验回归方程为z＝bx＋lna.根据散点图可知z与x正相关，所以b＞0.由回归直线图象可知，回归直线的纵截距大于0，即lna＞0，所以a＞1.
　　　 　对于A，回归分析中，样本相关系数绝对值越大，拟合效果越好，A不正确；对于B，由y＝c·ekx两边取对数得lny＝kx＋lnc，由题意知k＝0.3，lnc＝4，即c＝e4，B正确；对于C，由公式知，C正确．
6．为了研究某种病毒在特定环境下随时间变化的繁殖情况，得到了一些数据，绘制成散点图，发现用模型y＝cekx拟合比较合适．令z＝lny，得z＝1.3x＋a，经计算发现x，z满足下表，则(　 　)A．c＝e－0.2　　B．k＝1.3C．c＝e0.2　　D．k＝－1.3
由z＝lny，y＝cekx，得z＝ln(cekx)＝kx＋lnc，所以k＝1.3，lnc＝a＝－0.2，即c＝e－0.2.
9．2020年初，从非洲蔓延到东南亚的蝗虫灾害严重威胁了国际农业生产，影响了人民生活．世界性与区域性温度的异常、旱涝频繁发生给蝗灾发生创造了机会．已知蝗虫的产卵量y与温度x的关系可以用模型y＝c1ec2x拟合，设z＝ln y，其变换后得到一组数据如下表：由上表可得线性回归方程z＝0.2x＋a，则c1＝________.
四、 解答题(让规范成为一种习惯)10．(2022·聊城模拟)某校高二年级发起了“发扬奥林匹克精神，锻炼健康体魄”的年度主题活动，经过一段时间后，学生的身体素质明显提高．
(1) 为了解活动效果，该年级对开展活动以来近6个月体重超重的人数进行了调查，调查结果统计如图所示，根据散点图可以认为散点集中在曲线y＝ebx＋a的附近，请根据下表中的数据求出该年级体重超重人数y与月份x之间的回归方程(系数a和b的最终结果精确到0.01)，并预测从开展活动以来第几个月份开始该年级体重超标的人数降至10人以下；
(2) 在某次足球训练课上，球首先由A队员控制，此后足球仅在A，B，C三名队员之间传递，假设每名队员控球时传给其他队员的概率如下表所示：
若传球3次，记B队员控球次数为X，求X的分布列及均值．
11．(2022·梅州模拟)某市某医疗器械公司转型升级，从9月1日开始投入呼吸机生产，该公司9月1日～9月9日连续9天的呼吸机日生产量为yi(单位：百台，i＝1,2，…，9)，数据作了初步处理，得到如图所示的散点图．
(1) 从9个样本点中任意选取2个，在2个样本点的生产量都不高于300台的条件下，求2个样本点都高于200台的概率；
(2) 由散点图分析可知，样本点都集中在曲线y＝ln(bt＋a)的附近，求y关于t的方程y＝ln(bt＋a)，并估计该公司从生产之日起需要多少天呼吸机日生产量可超过500台．参考数据：e5≈148.4.
由y＝ln(4t－1)＞5⇒4t－1＞e5≈148.4⇒t＞37.35，所以需要38天呼吸机日生产量可超过500台．
　　　　 (1) 因为AB∥CD，CD⊂平面PCD，AB⊄平面PCD，所以AB∥平面PCD.又AB⊂平面PAB，平面PAB∩平面PCD＝l，所以AB∥l.