






备战2024年高考总复习一轮(数学)第6章 数列 第4节 数列求和课件PPT
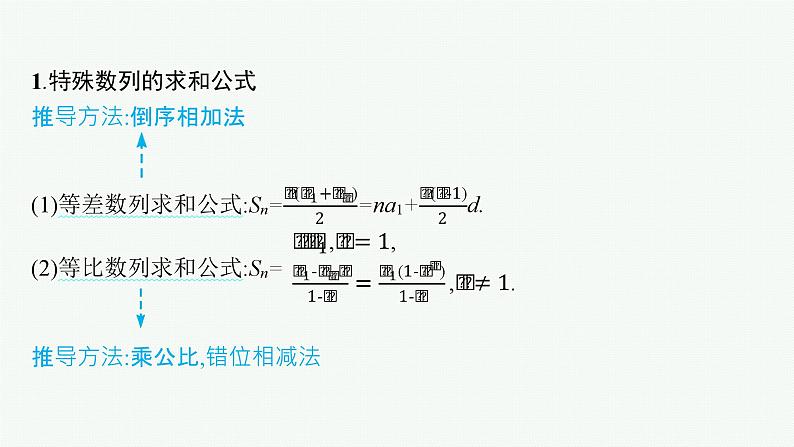
展开1.特殊数列的求和公式 推导方法:倒序相加法
推导方法:乘公比,错位相减法
2.非特殊数列求和的几种常用方法(1)倒序相加法:如果一个数列{an}的前n项中与首末两端等“距离”的两项的和相等,那么求这个数列的前n项和即可用倒序相加法,如等差数列的前n项和公式即是用此法推导的.(2)分组求和法:一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成,则求和时可用分组求和法,分别求和后再相加减.如已知an=2n+(2n-1),求Sn.(3)并项求和法:若一个数列的前n项和中两两结合后可求和,则可用并项求和法.如已知an=(-1)nf(n),求Sn.
错位相减时,要注意最后一项的符号(4)错位相减法:如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的,那么这个数列的前n项和即可用错位相减法来求,如等比数列的前n项和公式就是用此法推导的.(5)裂项相消法:把数列的通项公式拆成两项之差,在求和时中间的一些项可以相互抵消,从而求得其和.
微点拨常见的裂项公式:
常用结论2个常用求和公式
例1(2022河南郑州三模)已知数列{an}满足a1=1,an+1=Sn+1,其中Sn为数列{an}的前n项和,n∈N*.(1)求数列{an}的通项公式;(2)设数列{bn-an}是首项为1,公差为2的等差数列,求数列{bn}的前n项和.
解:(1)a1=1,an+1=Sn+1,当n=1时,可得a2=a1+1=2.当n≥2时,an=Sn-1+1,则an+1-an=an,即an+1=2an,且a2=2a1.故{an}是以1为首项,2为公比的等比数列,所以an=2n-1.(2)由题意bn-an=1+2(n-1)=2n-1,所以bn=2n-1+2n-1,设{bn}的前n项和为Tn,
规律方法 1.分组转化法求和数列求和应从通项公式入手,若无通项公式,则先求通项公式,然后通过对通项公式变形,转化为等差数列或等比数列或可求前n项和的数列求和.2.分组转化法求和的常见类型
对点训练1已知数列{an}的各项均为正数,其前n项和为Sn,an=1-2Sn.(1)求数列{an}的通项公式;
例2数列{an}满足a1=1,点(n,an+an+1)在函数y=kx+1图象上,其中k为常数,且k≠0.(1)若a1,a2,a4成等比数列,求k的值;(2)当k=3时,求数列{an}的前n项和Sn.
解:(1)由an+an+1=kn+1可得a1+a2=k+1,a2+a3=2k+1,a3+a4=3k+1,因为a1=1,所以a2=k,a3=k+1,a4=2k,又a1,a2,a4成等比数列,所以 =a1a4,则k2=2k,又k≠0,故k=2.
(2)当k=3时,an+an+1=3n+1,当n为偶数时,Sn=(a1+a2)+(a3+a4)+(a5+a6)+…+(an-1+an)
规律方法 若一个数列的前n项和中两两结合后可求和,则可用并项求和法.如已知an=(-1)nf(n),求Sn.
对点训练2记数列{an}的前n项和为Sn,已知Sn=2an-2n+1.(1)求数列{an}的通项公式;
解:(1)当n=1时,由Sn=2an-2n+1,可得a1=S1=2a1-2+1,即有a1=1.当n≥2时,an=Sn-Sn-1=2an-2n+1-2an-1+2(n-1)-1,即an=2an-1+2,可得an+2=2(an-1+2),显然an-1+2≠0.所以数列{an+2}是首项为3,公比为2的等比数列,则an+2=3·2n-1,即有an=3·2n-1-2.
规律方法 1.基本步骤
2.裂项原则一般是前边裂几项,后边就裂几项,直到发现被消去项的规律为止.3.消项规律消项后前边剩几项,后边就剩几项,前边剩第几项,后边就剩倒数第几项.
例5. 已知数列{an}的前n项和为Sn,若Sn=-n2+kn(k∈N*),且Sn的最大值为25.(1)求k的值及通项公式an;
规律方法 错位相减法求数列{an}的前n项和的步骤与注意事项(1)适用条件若{an}是公差为d(d≠0)的等差数列,{bn}是公比为q(q≠1)的等比数列,求数列{anbn}的前n项和Sn.
(3)注意事项①在写出Sn与qSn的表达式时,应特别注意将两式“错位对齐”,以便下一步准确写出Sn-qSn;②作差后,应注意减式中所剩各项的符号要变号.
若选②:因为Sn=3×2n-3,①所以当n=1时,a1=S1=3×2-3=3,当n≥2时,Sn-1=3×2n-1-3,②①-②得an=Sn-Sn-1=3×2n-3×2n-1=3×2n-1(n≥2),因为a1=3符合上式,所以an=3×2n-1.所以bn=3n×2n-1.以下解法同选①.若选③:由 =anan+2知数列{an}是等比数列,设数列{an}的公比为q,则a4=a1q3,即24=3q3,所以q3=8,解得q=2,所以an=3·2n-1.所以bn=3n·2n-1.以下解法同选①.
高考数学一轮总复习课件第4章数列第4讲数列求和(含解析): 这是一份高考数学一轮总复习课件第4章数列第4讲数列求和(含解析),共43页。PPT课件主要包含了2裂项相消法,3错位相减法,4倒序相加法,名师点睛,题组一走出误区,答案BCD,答案A,题组三真题展现,答案4,变式训练等内容,欢迎下载使用。
备战2024年高考总复习一轮(数学)第6章 数列 解答题专项三 数列课件PPT: 这是一份备战2024年高考总复习一轮(数学)第6章 数列 解答题专项三 数列课件PPT,共37页。
备战2024年高考总复习一轮(数学)第6章 数列 第2节 等差数列课件PPT: 这是一份备战2024年高考总复习一轮(数学)第6章 数列 第2节 等差数列课件PPT,共30页。PPT课件主要包含了内容索引,强基础固本增分,研考点精准突破,第2项,同一个常数,等差中项,a1+n-1d等内容,欢迎下载使用。












