数学人教A版 (2019)6.4 平面向量的应用图文ppt课件

这是一份数学人教A版 (2019)6.4 平面向量的应用图文ppt课件，共37页。PPT课件主要包含了学习目标，一创设问题情境，如何测量呢，探究新知，正弦定理的推导，外接圆法，4正弦定理，定理结构特征，巩固新知，课堂检测等内容，欢迎下载使用。
借助向量的运算,探索三角形边长与角度的关系; 2.掌握正弦定理，并能利用正弦定理解三角形、判 断三角形解的个数问题；3.能利用正弦、余弦定理解决三角形中边与角的关系;4.掌握正弦、余弦定理的简单应用.5.核心素养：数学抽象、数学建模、数学运算.
任务：测量壶口瀑布壶口 处的距离AB.工具：卷尺，测角仪.
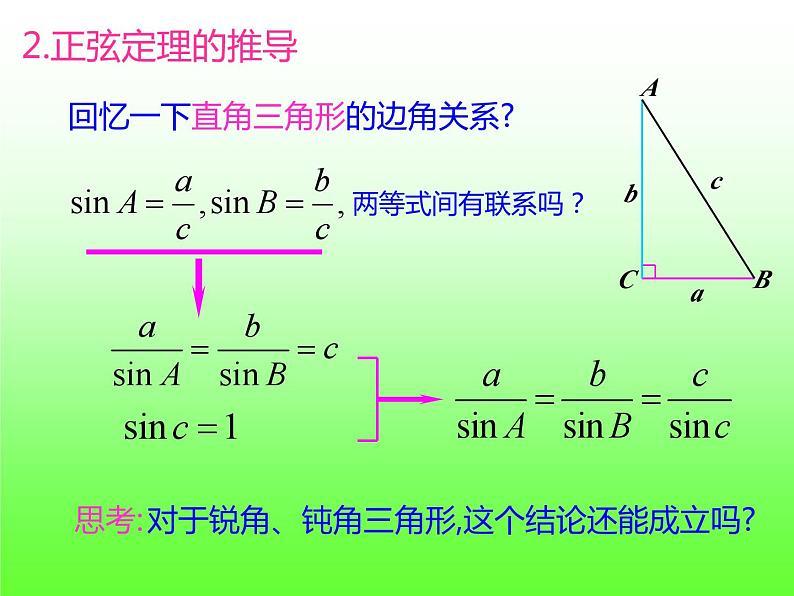
余弦定理及其推论分别给出了已知两边及其夹角、已知三边直接解三角形的公式.如果已知两角和一边，是否也有相应的直接三角形的公式呢？
向量是数量积运算中出现了角的余弦,而我们需要的是角的正弦，如何实现转化？
回忆一下直角三角形的边角关系?
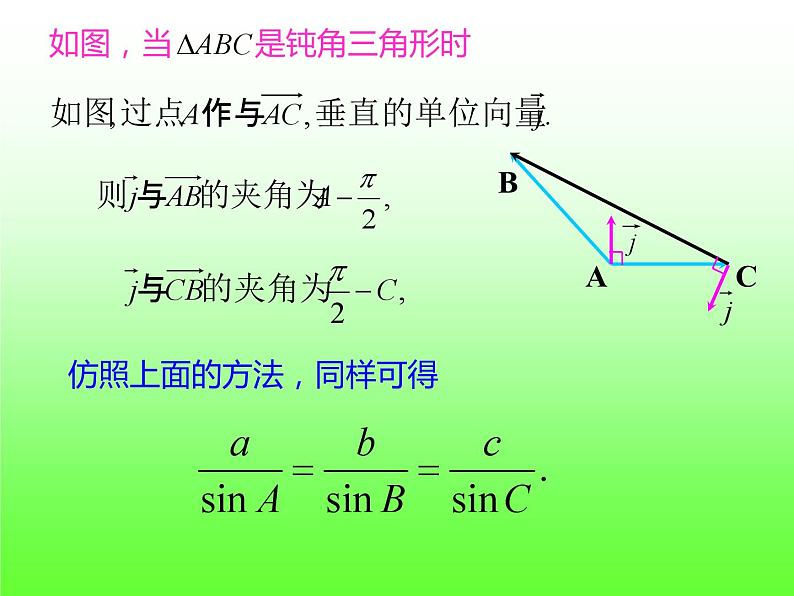
仿照上面的方法，同样可得
如图，当 是钝角三角形时
3.思考:还有其他证明的方法吗？
含三角形的三边及三内角,由己知二角一边 或二边一角可表示其它的边和角.
在一个三角形中,各边和它所对角的 正弦的比相等,即
5.剖析定理、加深理解
(1).A+B+C=π.
(2).大角对大边，大边对大角.
2).一般地，把三角形的三个角A，B，C和它们的对边 a，b，c叫做三角形的元素。已知三角形的几个元 素求其他元素的过程叫解三角形
3).正弦定理可以解决三角形中的问题：
(1).已知两边和其中一边的对角,求另一边的对角, 进而 可求其他的边和角
(2).已知两角和一边，求其他角和边
6.正弦定理的变形公式
(1)已知两角和任一边，求其他两边和一角
在△ABC 中,已知c = 10,A = 45。, C = 30。,解三角形.
解:根据三角形内角和定理，
(2)已知两边和其中一边的对角,求其它边和角.
（三角形中大边对大角）
5.例9.根据下列条件,判断△ABC的形状.
直角三角形或等腰三角形
1.本节课你学习了哪些基本知识？
2.本节课你学会了哪些思想方法？
数形结合思想、化归转化思想
作业：(1)课本P48 练习 2、3题 (2)做完《一线课堂》对应习题
9.探究:引入时黄河壶口瀑布问题的解决方法
具备下列哪个条件可以直接使用正弦定理解三角形?
已知两角一边，可求其它边和角！
已知两边一对角，可求其它边和角！
(2),(4),(5)
(1)b=11, a=20, B=30 (2)c=54, b=39, C=120 (3)b=26, c=15, C=30 (4)a=2,b=6,A=30
6.例3.判断满足下列的三角形的个数:
2).若A为直角或钝角时:
7.已知a,b和A用正弦定理求B时的各种情况
10.例4.根据下列条件,判断△ABC的形状.
试判断△ABC的形状.
2.正弦定理可以解决三角形中的问题：
3.实现三角形当中边角之间的转化
作业：课本P48 练习 2、3题
2.△ABC的三个内角A,B,C对应的三边长分别
②若 求 和b的值.