云南省玉溪市江川区教育科学研究所2023年数学六年级第二学期期末复习检测模拟试题含解析

云南省玉溪市江川区教育科学研究所2023年数学六年级第二学期期末复习检测模拟试题

一、认真填一填。

1．（____）个是；           里有（____）个；

2．0.36里面有（_____）个，化成分数是（______），再添上（_____）个就是最小的质数．

3．一个正方形面积是20平方厘米，从这个正方形上剪下一个最大的圆，这个圆的面积是（______）平方厘米。

4．一条长9米的绳子平均分成4段，每段占全长的（________），每段长（________）米。

5．一个钟面被分成两部分(如图)，较小部分占整个钟面的，圆心角是（_________），较大部分占整个钟面的，圆心角是（_________）．

6．一个直角三角形（如下图），它的三条边长分别是10厘米、8厘米和6厘米，它的面积是（_____）平方厘米。

7．有15盒饼干，其中的14盒质量相同，另有1盒少了几块，如果能用天平称，那么至少称_____次可以报纸找出这盒饼干．

8．在、、0.277、27.2这四个数中，最大的数是（______），最小的数是（______）。

9．一个正方体的棱长和是48厘米，这个正方体的体积是________

10．把一条3米长的绳子平均分成5段，每段是这条绳子的____，每段是_____米．

二、是非辨一辨。

11．圆的周长一定时，直径越大，圆周率就越小。（______）

12．一个数是12的倍数，它也一定是6和4的倍数。  （_______）

13．因为，所以5.7是1.9的3倍，也可以说5.7是1.9的倍数。（________）

14．大于而小于的分数只有。（______）

15．可以化成有限小数．   （_____）

16．两个合数的和一定是偶数．（_____）

三、细心选一选。请把正确答案的序号填在括号里。

17．一个正方体的木料，它的底面积是10平方厘米，把它横截成4段相同的长方体，表面积增加（    ）平方厘米。

A．60                                             B．40                                C．30

18．一堆煤，已经烧了吨，还剩全部的没烧，已经烧了的和没烧的相比（      ）

A．已烧的多 B．没烧的多 C．一样多 D．无法确定

19．一个合数至少有（    ）个因数。

A．4 B．2 C．3 D．1

20．把一个平行四边形分成甲、乙、丙3个三角形，丙的面积是甲乙面积之和的（    ）。

A． B． C． D．

21．在解决下面问题的过程中，没有运用转化策略的是（      ）。

A．计算异分母分数加减法时，先通分。

B．推导圆面积计算公式时，把圆剪拼成近似长方形。

C．用竖式计算整数加减法。

22．小东从一个长方体纸盒上撕下两个相邻的面（展开图如图，单位：厘米），这个纸盒的体积是（    ）立方厘米。

A．不确定 B．18 C．21 D．126

四、用心算一算。

23．直接写得数．

＋＝         －＝          -=        1－－=        

+=           －＝          2-=        ++=

24．计算下面各题，怎样算简便就怎么算．

－(＋)          －＋          －＋－ 

＋－          ＋＋＋        ＋＋＋＋

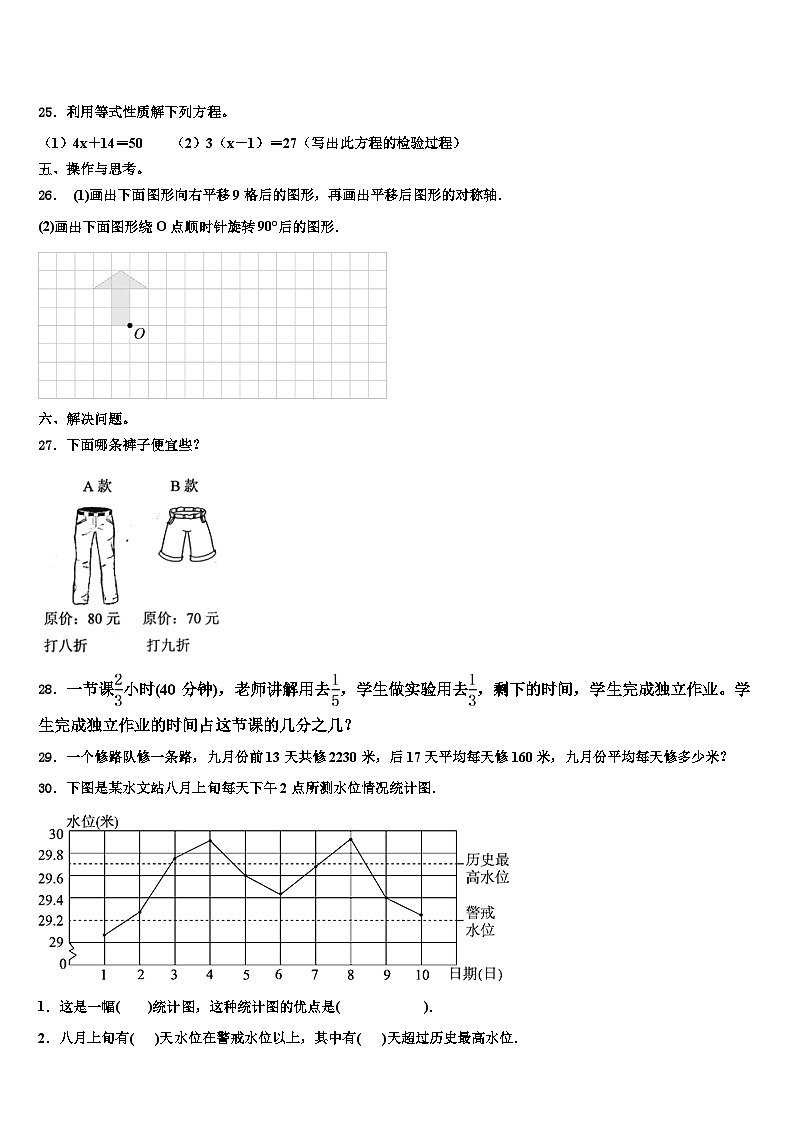
25．利用等式性质解下列方程。   

（1）4x＋14＝50    （2）3（x－1）＝27（写出此方程的检验过程）

五、操作与思考。

26． (1)画出下面图形向右平移9格后的图形，再画出平移后图形的对称轴．

(2)画出下面图形绕O点顺时针旋转90°后的图形．

六、解决问题。

27．下面哪条裤子便宜些？

28．一节课小时(40分钟)，老师讲解用去，学生做实验用去，剩下的时间，学生完成独立作业。学生完成独立作业的时间占这节课的几分之几？

29．一个修路队修一条路，九月份前13天共修2230米，后17天平均每天修160米，九月份平均每天修多少米？

30．下图是某水文站八月上旬每天下午2点所测水位情况统计图．

1．这是一幅(    )统计图，这种统计图的优点是(            )．

2．八月上旬有(   )天水位在警戒水位以上，其中有(   )天超过历史最高水位．

3．在24小时内，水位上涨最快的是八月(    )日至八月(    )日，在48小时内，水位变化最小的是八月(    )日至八月(    )日．

4．从图中你还能得到什么信息?

31．王大伯有一块长方形的花圃地，用其中的种玫瑰花，种郁金香，剩下的部分种杜鹃花，种杜鹃花的面积占总面积的几分之几？

32．小亮到少年宫的距离是2198米，他骑一辆车轮外直径约是70厘米的自行车去少年宫。如果车轮每分钟转100圈，小亮骑这辆车去少年宫需要多少分？

33．李师傅用木条做一个长8cm，宽4cm，高5cm的长方体框架，至少需要（　　）长的木条．

A．17cm B．34cm C．68cm

参考答案

一、认真填一填。

1、6    3   

【解析】略

2、36        164   

【详解】略

3、15.7

【分析】由题意可知：这个最大圆的直径应等于正方形的边长，设圆的半径为r厘米，则圆的面积＝r2，又因（2r）2＝20平方厘米，于是可以求出r2的值，由此计算得解。

【详解】设圆的半径为r厘米，

则正方形的面积∶

（2r）2＝20

4r2＝20

r2 ＝5

圆面积：3.14×5＝15.7（平方厘米）
故答案为：15.7

本题考查圆的面积的应用，关键是得出正方形边长与圆半径的关系，根据正方形的面积求出圆的半径的平方。

4、       

【分析】要求每段占全长的几分之几，是把这条绳子的长度看作单位“1”，把它平均分成4份，每份占全长的；这根绳子平均分成4段，求每段的长度，用除法即可；

【详解】1÷4＝

9÷4＝（米）

故答案为：；

本题主要是考查分数的意义，把单位“1”平均分成若干份，用分数表示时，分母是分成的份数，分子是要表示的份数。

5、       

【详解】略

6、24

【解析】略

7、1

【详解】第一次：从15盒饼干中，任取10盒，平均分成2份，每份5盒，分别放在天平秤两端，若天平秤平衡，则少几块的那盒即在未取的5盒中（再按照下面方法操作），若不平衡；第二次：从在天平秤较高端的5盒饼干中，任取4盒，平均分成2份，每份2盒，分别放在天平秤两端，若天平秤平衡，则少几块的那盒即在未取的1盒中（再按照下面方法操作），若不平衡；第三次：把在天平秤较高端的2盒饼干，分别放在天平秤两端，天平秤较高端的饼干即为少几块的饼干，

故答案为1．

8、27.2       

【分析】将分数化为小数，用分子直接除以分母，然后按照小数比较大小的方法，即先看它们的整数部分，整数部分大的那个数就大；如果整数部分相同，十分位上的数大的那个数就大；如果十分位上相同，百分位上的数大的那个数就大，以此类推。

【详解】27.2＞≈0.2778＞0.277＞

此题主要考查学生对小数比较大小方法的掌握与应用，其中需要掌握分数化小数的方法。

9、64立方厘米

【解析】【考点】长方体和正方体的体积  

【解答】解：48÷12=4(厘米)，体积：4×4×4=64(立方厘米)

故答案为：64立方厘米

【分析】用正方体的棱长和除以12即可求出正方体的棱长，用棱长乘棱长乘棱长求出正方体的体积即可.

10、    0.6   

【分析】求每段长是这根绳子的几分之几，平均分的是单位“1”，求的是分率；求每段长的米数，平均分的是具体的数量3米，求的是具体的数量；都用除法计算．

【详解】1÷5=

3÷5=0.6（米）

答：每段是这条绳子的，每段长0.6米．

二、是非辨一辨。

11、×

【分析】圆周率是圆的周长与直径的比值，是一个固定不变的数，不随直径的变化而变化，据此判断即可。

【详解】圆周率＝圆的周长÷直径，因为圆周率是一个定值，所以周长一定时，直径也一定，故原题说法错误。

故答案为：×

本题考查对圆周率的认识，需掌握圆周率的定义。

12、√

【解析】略

13、×

【分析】根据因数和倍数的意义：如果整数a能被整数b整除（b≠0），a就叫做b的倍数，b就叫做a的因数；据此判断即可。

【详解】因为，所以5.7是1.9的3倍，但5.7和1.9都不是整数，所以不能说5.7是1.9的倍数。

故答案为：×

此题考查了因数和倍数的意义，注意基础知识的理解，只在整数范畴探讨因数和倍数。

14、×

【分析】根据分数的基本性质：分数的分子和分母同时乘或除以相同的数（0除外），分数的大小不变。举例说明即可。

【详解】=，=

大于而小于的分数还有、等，所以原题说法错误。

故答案：×。

本题考查了分数的基本性质，两个分数之间有无数个分数。

15、√

【解析】略

16、×

【解析】合数中既有奇数也有偶数，其中奇数+奇数=偶数，奇数+偶数=奇数，偶数+偶数=偶数，所以两个合数的和可能是奇数也有可能是偶数．

三、细心选一选。请把正确答案的序号填在括号里。

17、A

【分析】横截成4段相同的长方体，截了3次，相当于多了2×3＝6个横截面，也就是6个10平方厘米；据此解答。

【详解】10×6＝60（平方厘米）

故选：A

本题主要考查了正方体的表面积，关键是要理解将正方体截成长方体后，表面积是增加了的，增加的截面个数＝截的次数×2。

18、B

【解析】略

19、C

【分析】一个数，除了1和它本身以外，还要别的因数，这样的数叫做合数。

【详解】一个合数至少有3个因数。

故答案为：C。

本题考查的目的是理解掌握合数的意义。

20、A

【分析】根据图示可以看出甲、乙、丙的面积和正好是平行四边形的面积，乙丙的面积和就是甲的面积，即甲的面积是2＋3＝5，甲乙的面积和就是3＋5＝8，用丙的面积除以甲乙的面积即可。

【详解】2÷（2＋3＋3）

＝2÷8

＝

此题考查的是分数的意义，解题时注意各部分之间的关系。

21、C

【分析】根据题意，逐项判断是否有转化步骤，再进行选择。

【详解】A．异分母分数加减法，需要先通分，把分母化为一样，再进行计算，运用了转化策略；

B．推导圆面积计算公式时，把圆剪拼成近似长方形，运用了转化策略；

C．用竖式计算整数加减法，不用转化。

故答案为：C

此题主要考查学生对转化策略的认识与判断。

22、D

【分析】看图可知，长方体的长是6厘米，宽是3厘米，高是7厘米，据此根据长方体体积公式计算即可。

【详解】6×3×7＝126（立方厘米）

故答案为：D

本题考查了长方体体积，长方体体积＝长×宽×高。

四、用心算一算。

23、  0      

【详解】略

24、 ; ;

;2;

【详解】略

25、（1）x＝9；（2）x＝10

【分析】（1）方程两边同时减去14，再同时除以4即可；

（2）方程两边同时除以3，再同时加上1即可；要将求出的未知数值代入原方程，分别计算等号左右两边的结果，如果两边相等，则为原方程的解；如不相等，则不是原方程的解。

【详解】（1）4x＋14＝50

解：4x＋14－14＝50－14

4x＝36

4x÷4＝36÷4

x＝9

（2）3（x－1）＝27

解：3（x－1）÷3＝27÷3

x－1＝9

x－1＋1＝9＋1

x＝10 

检验：将x＝10带入原方程

左边＝3（10－1）＝3×9＝27

右边＝27

左边＝右边

所以x＝10是原方程的解。

解方程要掌握等式的性质，即等式两边同时加上或减去同一个数，左右两边仍然相等；等式两边同时乘或除以同一个不是0的数，等式两边仍然相等。

五、操作与思考。

26、（1）（2）题见下图:

【解析】略

六、解决问题。

27、B款便宜

【分析】打几折出售就是按原价的百分之几十出售，由此分别计算出打折后的价钱，比较即可。

【详解】80×80%＝64（元）

70×90%＝63（元）

64＞63，B款便宜

答：B款裤子便宜些。

本题主要考查简单的折扣问题，理解折扣的意义是解题的关键。

28、1－－＝

答：学生完成独立作业的时间占这节课的。

【解析】略

29、（2230+160*17）/30=165

【解析】略

30、1．折线 不但能知道数量的多少，而且可以清楚地看出数量的增减变化趋势

2．9 3

3．2 3 5 7

4．答案不唯一：如八月1日至八月4日的水位呈上升趋势。

【解析】略

31、

【分析】把王大伯这块长方形的花圃地看作单位“1”，用单位“1”分别先后减去玫瑰花所占的，郁金香所占的，剩下的就是杜鹃花所占的分率。

【详解】

答：种杜鹃花的面积占总面积的。

本题是异分母分数减法应用题，计算时需要将各个分数通分再相减，计算后的结果要约分。

32、10分钟

【解析】70厘米=0.7米

2198÷（3.14×0.7×100）

=2198÷219.8

=10（分钟）

33、C

【解析】（8+4+5）×4

＝17×4

＝68（厘米）

答：至少需要68厘米长的木条．

故选：C．