浙江省绍兴市嵊州市城关中学六校联考2023届九年级下学期5月模拟数学试卷及答案

这是一份浙江省绍兴市嵊州市城关中学六校联考2023届九年级下学期5月模拟数学试卷及答案，共11页。
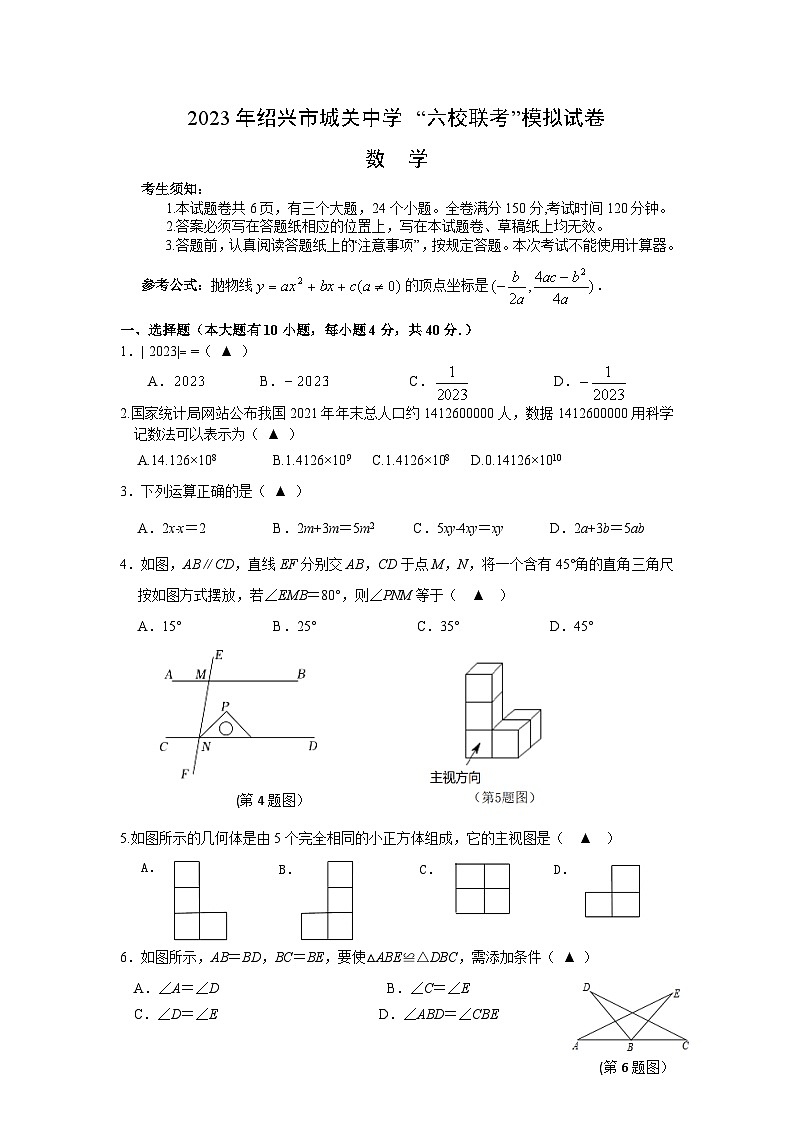
2023年绍兴市城关中学 “六校联考”模拟试卷数  学考生须知：    1.本试题卷共6页，有三个大题，24个小题。全卷满分150分,考试时间120分钟。    2.答案必须写在答题纸相应的位置上，写在本试题卷、草稿纸上均无效。3.答题前，认真阅读答题纸上的“注意事项”，按规定答题。本次考试不能使用计算器。参考公式：抛物线的顶点坐标是．一、选择题（本大题有10小题，每小题4分，共40分．）1．|2023 |=（ ▲ ）A．     B．           C．            D．2.国家统计局网站公布我国2021年年末总人口约1412600000人，数据1412600000用科学记数法可以表示为（ ▲ ）A.14.126×108 B.1.4126×109   C.1.4126×108   D.0.14126×10103．下列运算正确的是（ ▲ ）A．2x﹣x＝2 B．2m+3m＝5m2 C．5xy﹣4xy＝xy  D．2a+3b＝5ab4．如图，AB∥CD，直线EF分别交AB，CD于点M，N，将一个含有45°角的直角三角尺按如图方式摆放，若∠EMB＝80°，则∠PNM等于（　▲　）A．15° B．25°  C．35°  D．45°      5.如图所示的几何体是由5个完全相同的小正方体组成，它的主视图是（　▲　）                                6．如图所示，AB＝BD，BC＝BE，要使△ABE≌△DBC，需添加条件（ ▲ ）A．∠A＝∠D                        B．∠C＝∠E C．∠D＝∠E                      D．∠ABD＝∠CBE                                                                                          7.方程2x2—3x—4=0的解，可看成以下两个函数图象交点的横坐标，其中正确的个数是（ ▲  ）       A． 4               B． 3        C． 2     D． 1①②③④8．为迎接亚运，某校购买了一批篮球和足球，已知购买足球的数量是篮球的2倍，购买足球用了5000元，购买篮球用了4000元，篮球单价比足球贵30元，根据题意可列方程，则方程中关于x的含义理解正确的是（ ▲　）A．篮球有x个 B．每个篮球x元      C．足球有x个 D．每个足球x元9．如图，已知直线l1与x轴，y轴分别相交于点A,M，与直线y=4相交于点C，直线l2 y=kx+2与直线y=4相交于点B，与x轴相交于点D.已知E(0.5，0),F(3,0),当点D从点E运动到点F的过程中，四边形ABCD的形状变化依次为（ ▲　）A.平行四边形→矩形→平行四边形→正方形→平行四边形B. 平行四边形→矩形→平行四边形→菱形→平行四边形C.平行四边形→菱形→平行四边形→矩形→平行四边形D．平行四边形→正方形→平行四边形→矩形→平行四边形10.有9个形状大小相同的小球,其中一个略重些,其余8个重量相同.现给你一架天平,能将那个略重些的小球找到，则至少需要天平的次数是(  ▲  )A．4       B．3          C．2         D．1二、填空题（本大题有6小题，每小题5分，共30分）11．分解因式：a2 – 4＝　▲　．12.关于x的不等式3（x-1)<12的解集是　▲　．13.我国古代的《洛书》中记载了最早的幻方——九宫图.将数字1-9分别填入如图所示的幻方中，要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15，则m的值为      .14.在菱形ABCD中，分别以点C和点D为圆心，大于CD为半径作弧，两弧交于点M，N，直线MN与直线BD交于点E,且∠ECB＝63°，则∠ABC的值是　 ▲   ．15.如图，在Rt△ABC中，AB=CB,直角顶点B在y轴上，边AB交x轴于点D（，0），点C的坐标为（﹣4，0），反比例函数（k≠0）的图象过点A，则k的值是　▲　．16.如图，矩形ABCD中，AB=6，AD=10.动点E在AB边上，，     以点E为圆心，以BE为半径作弧，点G是弧上一动点.（1） 如图①，若点E与点A重合，且点F在BC上，当 DF与弧相切于点G时，则BF的值是　▲　；（2）如图②，若AE=1连结CG,DG,分别取DG、CG的中点P、Q，连接PQ，M为PQ的中点，则CM的最小值为 　▲　．             三、解答题（本大题有8小题，第17～20小题每小题8分，第21小题10分，第22，23小题每小题12分，第24小题14分，共80分．）17.(1)计算：|﹣|﹣（4﹣π）0-2sin60°+（）﹣1．      (2) 解方程组    18.如图，在平行四边形ABCD中，E，F分别是边AD，BC上的点，且．（1）判定BE与DF是否相等，并说明理由；（2）连结AF，若，，求的度数． 19.我市有A，B，C，D，E五个景区很受游客喜爱．一旅行社对某小区居民在暑假期间去以上五个景区旅游（只选一个景区）的意向做了一次随机调查统计，并根据这个统计结果制作了如下两幅不完整的统计图：（1）直接写出本次随机调查的总人数，并补全条形统计图；（2）若该小区有居民1200人，试估计去B地旅游的居民约有多少人？（3）小军同学已去过E地旅游，暑假期间计划与父母从A，B，C，D四个景区中，任选两个去旅游，求选到A，C两个景区的概率．（要求画树状图或列表求概率） 20.某校“综合与实践”活动小组的同学要测量AB，CD两座楼之间的距离，他们借助无人机设计了如下测量方案：无人机在AB，CD两楼之间上方的点O处，点O距地面AC的高度为66m，此时观测到楼AB底部点A处的俯角为70°，楼CD上点E处的俯角为30°，沿水平方向由点O飞行24m到达点F，测得点E处俯角为60°，其中点A，B，C，D，E，F，O均在同一竖直平面内．（1）求EF的长；（2）求楼AB与CD之间的距离AC的长．（参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75，≈1.73）． 21.如图,直线AC与⊙O相切于点C,射线AO与⊙O交于点D，E,连结CD.连结CE.(2)若AC=，AD=1，求弧CD的长.      22.“五一”假期，甲乙两人沿同一条笔直的马路同时从同一小区出发到“三味书屋”参观，小区与“三味书屋”的路程是4千米，甲骑自行车，乙步行，当甲从原路回到小区时，乙刚好到达“三味书屋”，图中折线O﹣A﹣B﹣C和线段OD分别表示两人离小区的路程s（千米）与所经过的时间t（分钟）之间的函数关系，请根据（图1）回答下列问题：（1）直接写出甲在“三味书屋”参观的时间；（2）求图中点P（OD与BC交点）的坐标，并解释该点坐标所表示的实际意义；（3）若两人之间的距离为y千米，当时，请在（图2）中画出y（千米）与所经过的时间t（分钟）之间的函数图象．     23. 在平面直角坐标系中，已知抛物线．（1）直接写出，当x取何值时，函数有最大或最小值是多少,（2）把抛物线沿着x轴方向平移，使得平移后的抛物线过点（0，-2），求平移的方向与距离；（3）点P(x1,y1),Q（x2,,y2)在抛物线上，其中．-3t，若对于x1,x2 ，都有y1>y2  ，求t的取值范围．    如图，在矩形ABCD中 ，BC=2AB=2 ，点M是对角线BD上一个动点，以直线CM为对称轴，点B的对称点为E点,连结DE与ME.（1）直接写出点C到直线BD的距离 ；（2）当点E落在矩形的边AD上时，求∠BCM的度数；（3）当△EMD为直角三角形时，求DE长.；                       2023年绍兴市城关中学 “六校联考”模拟试卷数学  参考答案一选择题：12345678910ABCCADADBC二填空题：   (a+2)(a-2)   12.       x<5    13.  9       14. 78°或162°   3.     16（1）. 2    （2）.17.(1)  3    （4分） ;(2)  （4分）18.(1) 略     （4分）       (2)  70°       (4分)19.解：（1）该小区居民在这次随机调查中被调查到的人数是20÷10%＝200（人），C景区人数为200﹣（20+70+20+50）＝40（人），补全条形图如下：     (1分)故答案为：200 (1分)     ，35(1分)       ；（2）估计去B地旅游的居民约有1200×35%＝420（人）；(2分)（3）画树状图如下：(2分)由树状图知，共有12种等可能结果，其中选到A，C两个景区的有2种结果，所以选到A，C两个景区的概率为．(2分)20（8分）解：（1）EF＝24m；                                          （4分）（2）延长AB，CD分别与直线OF交于点G和点H，在Rt△AGO中，∠AOG＝70°，∴OG＝≈＝24（m），在Rt△EFH中，∠HFE＝60°，∴FH＝EF•cos60°＝24×＝12（m），∴AC＝GH＝OG+OF+FH＝24+24+12＝60（m），∴楼AB与CD之间的距离AC的长约为60m．                 （4分）  21（10分） （1）如图，连结OC，∵直线AC与⊙O相切于点A，∴OC⊥CA，∴∠1+∠ACD=90º，∵ED为直径，∴∠1+∠2=90º，∴∠ACD=∠2，∴OE=OC，∴∠2 =∠E，∴∠ACD=∠E.                                     （5分）（2）设OD=OC=r∵OC⊥CA，AC=，AD=1,∴,∴r=1,∴tan∠AOC=，∴∠AOC=60º,∴.                                     （5分）22.（12分）解：（1）甲在南京博物院参观的时间为20分钟，            （2分）（2）求得直线OD的函数表达式为，当甲从图书馆返回时：设直线BC的函数表达式为s＝k1t+b．∵B（40，4），C（60，0），∴，  解得，∴直线BC的解析式为．                                   （2分）∴，解得t＝45．当t＝45时，．∴P（45，3）．                    （2分）答：P的坐标为（45，3），实际意义为当经过的时间为45分钟时，甲乙两人相遇，此时距离小区的路程为3千米．    （ 2分）（3）如图，即为y（千米）与所经过的时间（分钟）之间的函数图象．    （4分）  23.（12分）（2）当x=1值时，函数有最大是2,                     （3分  ）                                        （3）当=-2时，， =3， =-1;     向右平移1个单位或向左平移3个单位；           （3分）（4）法一∵=，=，又∵对于,都有>,∴>，∴<，∴<,∴,∴,∴或,∴或,∵∴或,   ∴或,∴.                                          法二：由图像的对称性可得：.                （6分） 24（14分）（1）C到直线BD的距离是2;                           （2分）  （2）如图，B、E关于CM对称，∴CE=CB=, ∠BCM=∠ECM，∵矩形ABCD，∴∠CDE=∠BCD=90º,∴COS∠DCE=，∴∠DCE=60º,∴∠BCE=30º,∴∠BCM=∠BCE=15º;   （6分）①    （3）当∠EDM=90º时，过点C作CF垂直ED交ED延长线于点F，在RT△DCH中，DC=，CH=2，∴DH=1，由题意得FD=CH=2，CF=DH=1,∵B、E关于CM对称，∴CE=CB=,在Rt△CEF中，，∴.                                        （2分）  ②当∠DME=90º时，如图，延长CM交AB于点N，则∠BME=90º，∵B、E关于CM对称，∴∠BMN=∠BME=45º，MB=ME，∴∠CMH=∠BMN=45º,在RT△CHM中，MH=CH=2，在RT△CDH中，DH==1, 在RT△CDB中，BD==5，∴DM=3，BM=2，∴ME=2，在Rt△DME中，DE=，                       （2分） ③当∠DEM=90º时，∵B、E关于CM对称，∴∠CEM=∠CBM,∵∠CEM=∠CED=90º, ∠CBM+∠BDC=90º, ∴∠CED=∠BDC,∵∠DCF=∠ECD,∴△DCF∽△ECD,∴，∴，∴CF=<2,∴不存在，舍去。                                         （2分）综上所述，当△AMD为直角三角形时，AD= 或AD=。