2020-2021学年江苏省苏州市高一（下）期末数学试卷

这是一份2020-2021学年江苏省苏州市高一（下）期末数学试卷，共28页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

2020-2021学年江苏省苏州市高一（下）期末数学试卷
一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）
1．（5分）的值为　　
A． B． C． D．
2．（5分）某工厂6名工人在一小时内生产零件的个数分别是11，12，13，15，15，18，设该组数据的平均数为，中位数为，则　　
A．， B．， C．， D．，
3．（5分）已知一个圆锥的母线长为2，其侧面积为，则该圆锥的高为　　
A．1 B． C． D．2
4．（5分）已知为虚数单位，是关于的方程的一个根，则　　
A． B．0 C．2 D．4
5．（5分）已知外接圆的圆心为，且，，则向量在向量上的投影向量为　　
A． B． C． D．
6．（5分）我省高考从2021年开始实行“”模式，“3”为全国统考科目语文、数学、外语，所有学生必考；“1”为首选科目，考生须在物理、历史两科中选择一科；“2”为再选科目，考生可在化学、生物、思想政治、地理4个科目中选择两科．高一学生小明和小亮正准备进行选科，假如他们首选科目都是物理，再选科目选择每个科目的可能性均相等，且选择互不影响，则他们的选科完全相同的概率为　　
A． B． C． D．
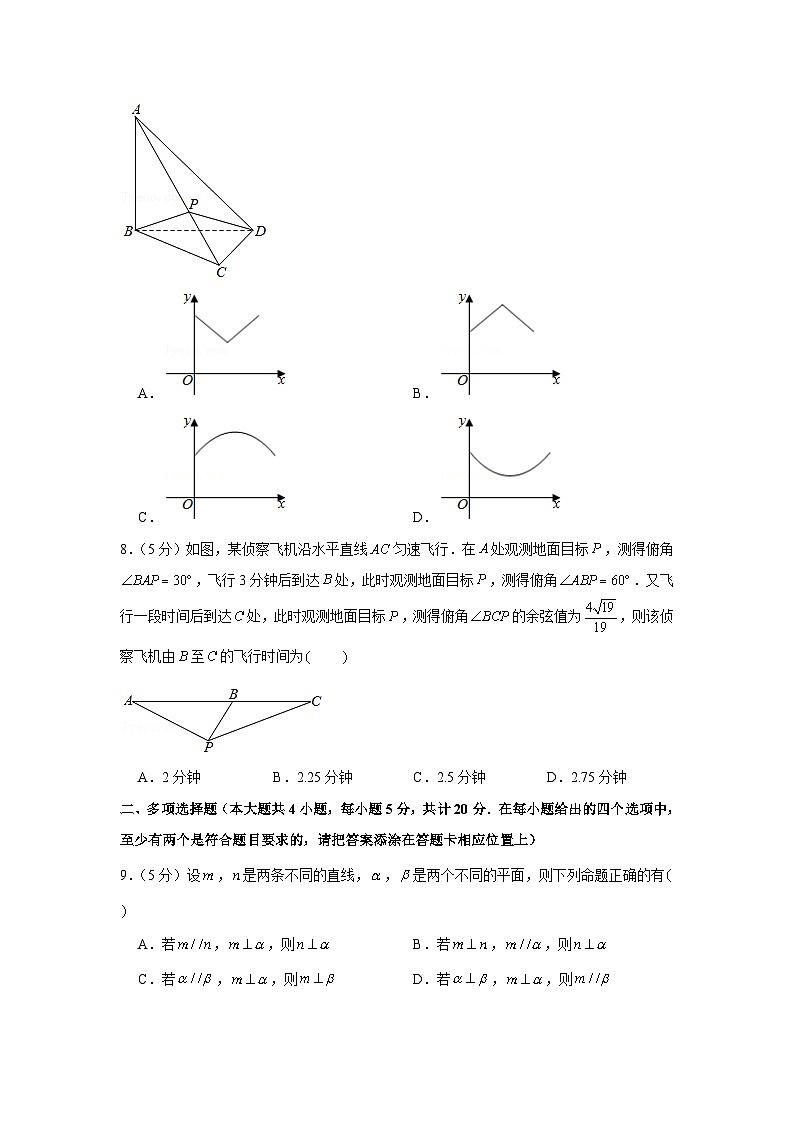
7．（5分）在《九章算术》中，将四个面都是直角三角形的四面体称为“鳖臑”．如图，在鳖臑中，平面，，，点在棱上运动．设的长度为，的面积为，则的大致图象是　　

A． B．
C． D．
8．（5分）如图，某侦察飞机沿水平直线匀速飞行．在处观测地面目标，测得俯角，飞行3分钟后到达处，此时观测地面目标，测得俯角．又飞行一段时间后到达处，此时观测地面目标，测得俯角的余弦值为，则该侦察飞机由至的飞行时间为　　

A．2分钟 B．2.25分钟 C．2.5分钟 D．2.75分钟
二、多项选择题（本大题共4小题，每小题5分，共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）
9．（5分）设，是两条不同的直线，，是两个不同的平面，则下列命题正确的有　　
A．若，，则 B．若，，则
C．若，，则 D．若，，则
10．（5分）已知为虚数单位，复数，则下列命题正确的有　　
A．若，则为实数
B．若，则为纯虚数
C．若，则实数的值为1
D．复数在复平面内对应的点不可能在第三象限
11．（5分）在中，若，，，则的面积可能为　　
A． B． C． D．
12．（5分）如图，在棱长为4的正方体中，，分别是，的中点，则　　

A．平面
B．二面角的正切值为
C．三棱锥的内切球半径为
D．过直线与平面平行的平面截该正方体所得截面的面积为18
三、填空题（本大题共4小题，每小题5分，共计20分．请把答案填写在答题卡相应位置上）
13．（5分）已知向量，，且，，若，，三点共线，则实数的值为 　　．
14．（5分）若复数在复平面内对应的点在第一象限内，且，则符合条件的一个复数为 　　．
15．（5分）若，则的值为 　　．
16．（5分）已知三棱锥中，平面，，异面直线与所成角的余弦值为，则三棱锥的体积为 　　，三棱锥的外接球的表面积为 　　．
四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）
17．（10分）为了解某市家庭用电量的情况，该市统计局调查了100户居民去年一年的月均用电量，发现他们的用电量都在至之间，进行适当分组后，画出频率分布直方图如图所示
（1）求的值；
（2）为了既满足居民的基本用电需求，又提高能源的利用效率，市政府计划采用阶梯式递增电价（第一档电量满足居民基本用电需求，电价最低；第二档电量反应正常合理用电需求，电价较高；第三档电量体现较高生活质量用电需求，电价最高）定价，希望使不少于的居民缴费在第一档，求第一档月均用电量的最低标准值（单位：．
18．（12分）如图，四棱柱的底面是正方形，侧面是菱形，，平面平面，，分别为，的中点．
（1）求证：平面；
（2）求与平面所成角的正切值．

19．（12分）在条件①；②；③中任选一个，补充在下面的问题中，并求解．
问题：的内角，，所对的边分别为，，，且_____．
（1）求角的大小；
（2）若，求角的大小．
20．（12分）如图，已知正方形的边长为2，为的中点．
（1）若为的中点，求的值；
（2）若为线段（不含端点）上的一个动点，请探究：当长为多少时，可使得最大？

21．（12分）如图，在中，已知，分别是，的中点，，，与交于点．
（1）若，求的值；
（2）若，求的长．

22．（12分）如图1，在矩形中，已知，，为的中点．将沿向上翻折，进而得到多面体—（如图．

（1）求证：；
（2）在翻折过程中，求二面角的最大值．

2020-2021学年江苏省苏州市高一（下）期末数学试卷
参考答案与试题解析
一、单项选择题（本大题共8小题，每小题5分，共计40分．在每小题给出的四个选项中，只有一个是符合题目要求的，请把答案添涂在答题卡相应位置上）
1．（5分）的值为　　
A． B． C． D．
【分析】利用二倍角公式进行解答．
【解答】解：．
故选：．
【点评】本题考查二倍角公式的运用，考查运算能力，属于基础题．
2．（5分）某工厂6名工人在一小时内生产零件的个数分别是11，12，13，15，15，18，设该组数据的平均数为，中位数为，则　　
A．， B．， C．， D．，
【分析】直接根据数据计算平均数与中位数即可．
【解答】解：根据题意，可得，
．
故选：．
【点评】本题考查平均数、中位数计算方法，考查数学运算能力，属于基础题．
3．（5分）已知一个圆锥的母线长为2，其侧面积为，则该圆锥的高为　　
A．1 B． C． D．2
【分析】先由圆锥的侧面积求出底面圆的半径，再根据勾股定理，得解．
【解答】解：设圆锥的母线为，底面圆的半径为，则，
因为侧面积为，所以，所以，
所以圆锥的高．
故选：．
【点评】本题考查圆锥中的简单计算，考查空间立体感和运算求解能力，属于基础题．
4．（5分）已知为虚数单位，是关于的方程的一个根，则　　
A． B．0 C．2 D．4
【分析】根据实系数一元二次方程的虚根成对原理，可得：也是原方程的一个虚根，利用根与系数的关系即可求出答案．
【解答】解：因为是关于的方程的一个根，
根据实系数一元二次方程的虚根成对原理，可得：也是原方程的一个虚根，
所以，
，
解得：，．
所以．
故选：．
【点评】本题考查了实系数一元二次方程的虚根成对原理、根与系数的关系，考查了推理与计算能力，是基础题．
5．（5分）已知外接圆的圆心为，且，，则向量在向量上的投影向量为　　
A． B． C． D．
【分析】根据条件作图可得为等边三角形，表示出所求投影即可
【解答】解：
外接圆圆心为的中点，即为外接圆的直径，如图：

又，所以为等边三角形，
，，
向量在向量上的投影为：．
故投影向量为，
故选：．
【点评】本题考查了平面向量数量积的性质及其运算，属中档题．
6．（5分）我省高考从2021年开始实行“”模式，“3”为全国统考科目语文、数学、外语，所有学生必考；“1”为首选科目，考生须在物理、历史两科中选择一科；“2”为再选科目，考生可在化学、生物、思想政治、地理4个科目中选择两科．高一学生小明和小亮正准备进行选科，假如他们首选科目都是物理，再选科目选择每个科目的可能性均相等，且选择互不影响，则他们的选科完全相同的概率为　　
A． B． C． D．
【分析】基本事件总数，他们的选科完全相同包含的基本事件个数，由此能求出他们的选科完全相同的概率．
【解答】解：高一学生小明和小亮正准备进行选科，
他们首选科目都是物理，再选科目选择每个科目的可能性均相等，且选择互不影响，
基本事件总数，
他们的选科完全相同包含的基本事件个数，
则他们的选科完全相同的概率为．
故选：．
【点评】本题考查概率的求法，考查古典概型、列举法等基础知识，考查运算求解能力，是基础题．
7．（5分）在《九章算术》中，将四个面都是直角三角形的四面体称为“鳖臑”．如图，在鳖臑中，平面，，，点在棱上运动．设的长度为，的面积为，则的大致图象是　　

A． B．
C． D．
【分析】作于点，作于点，连结，利用线面垂直的性质定理和判定定理证明平面，则，然后求出的解析式，由解析式确定函数的图象，即可得到答案．
【解答】解：如图，作于点，作于点，连结，因为平面，所以，即，
又，所以平面，所以，由题意可知，，，
设，则，，解得，
，所以，
则，
所以．
故选：．

【点评】本题考查了函数与立体几何的综合应用，主要考查了函数图象的识别，解题的关键是掌握识别图象的方法：可以从定义域、值域、函数值的正负、特殊点、特殊值、函数的性质等方面进行判断，考查了直观想象能力与逻辑推理能力，属于中档题．
8．（5分）如图，某侦察飞机沿水平直线匀速飞行．在处观测地面目标，测得俯角，飞行3分钟后到达处，此时观测地面目标，测得俯角．又飞行一段时间后到达处，此时观测地面目标，测得俯角的余弦值为，则该侦察飞机由至的飞行时间为　　

A．2分钟 B．2.25分钟 C．2.5分钟 D．2.75分钟
【分析】利用解三角形知识和三角函数关系式的恒等变换求解即可．
【解答】解：设飞机的飞行速度为，所以根据飞机的飞行图形，
测得俯角．飞行3分钟后到达处观测地面目标，测得俯角．
所以为直角三角形，
过点作于点，
则：，，，
解得：．
设，
由于，由同角三角函数的基本关系可得，
所以，
利用，解得．
故选：．

【点评】本题主要考查三角函数关系式的恒等变换，解三角形知识的应用，主要考查学生的运算能力和转换能力以及思维能力，属于中档题．
二、多项选择题（本大题共4小题，每小题5分，共计20分．在每小题给出的四个选项中，至少有两个是符合题目要求的，请把答案添涂在答题卡相应位置上）
9．（5分）设，是两条不同的直线，，是两个不同的平面，则下列命题正确的有　　
A．若，，则 B．若，，则
C．若，，则 D．若，，则
【分析】由直线与平面垂直的性质判断与；由空间中直线与直线、直线与平面、平面与平面的位置关系分析与．
【解答】解：若，，由直线与平面垂直的性质可得，故正确；
若，，则或或与相交，相交也不一定垂直，故错误；
若，，由直线与平面垂直的性质可得，故正确；
若，，则或，故错误．
故选：．
【点评】本题考查空间中直线与直线、直线与平面、平面与平面位置关系的判定，考查空间想象能力与思维能力，是基础题．
10．（5分）已知为虚数单位，复数，则下列命题正确的有　　
A．若，则为实数
B．若，则为纯虚数
C．若，则实数的值为1
D．复数在复平面内对应的点不可能在第三象限
【分析】直接利用复数的定义，复数的运算，复数的模，复数表示的几何意义判断、、、的结论．
【解答】解：复数，
对于：当时，，故为实数，故正确；
对于：当时，，故为纯虚数，故正确；
对于：若，故，解得，故错误；
对于：当复数在复平面内对应的点在第三象限时，得到，故不存在这样的，故正确．
故选：．
【点评】本题考查的知识要点：复数的定义，复数的运算，复数的模，复数表示的几何意义，主要考查学生的运算能力和数学思维能力，属于基础题．
11．（5分）在中，若，，，则的面积可能为　　
A． B． C． D．
【分析】根据条件及正弦定理即可求出，从而求出或，然后讨论时，得出的大小，然后即可求出的面积，同理可由时求出的面积．
【解答】解：在中，，，，
根据正弦定理得，解得，且，
，或，
①时，，
，
；
②时，，
，
．
故选：．
【点评】本题考查了正弦定理，三角形的面积公式，分类讨论的思想，考查了计算能力，属于基础题．
12．（5分）如图，在棱长为4的正方体中，，分别是，的中点，则　　

A．平面
B．二面角的正切值为
C．三棱锥的内切球半径为
D．过直线与平面平行的平面截该正方体所得截面的面积为18
【分析】中，连接，交于点，连接，利用向量法证明与不垂直，即与平面不垂直；
中，找出是二面角的平面角，计算即可；
中，利用等体积法求出三棱锥的内切球半径长；
中，取的中点，的中点，连接、、，四边形是过直线与平面平行的截面，可求出四边形的面积．
【解答】解：对于，如图1所示，

连接，，则，由平面，得平面，所以；
设交于点，连接，以矩形的底边为轴，为轴建立平面直角坐标系，如图2 所示：

则，，，，，
所以，，，则，
所以与不垂直，即与不垂直，
所以与平面不垂直，选项错误；
对于，是二面角的平面角，计算，
所以二面角的正切值为，选项正确；
对于，设三棱锥的内切球半径为，
则，
解答，所以三棱锥的内切球半径为，选项正确；
对于，如图3所示

取的中点，的中点，连接、、，
则四边形是过直线与平面平行的截面，且四边形是等腰梯形，
计算梯形的面积为，所以选项正确．
故选：．
【点评】本题考查了空间几何体的结构特征与应用问题，也考查了平行与垂直的判断问题和面积、体积的计算问题，是中档题．
三、填空题（本大题共4小题，每小题5分，共计20分．请把答案填写在答题卡相应位置上）
13．（5分）已知向量，，且，，若，，三点共线，则实数的值为 　3　．
【分析】先求出，，由，，三点共线，得，再求出实数的值．
【解答】解：向量，，且，，
，，，，
，
，，三点共线，，
，解得．
故答案为：3．
【点评】本题考查向量平行的性质，考查运算求解能力，是基础题．
14．（5分）若复数在复平面内对应的点在第一象限内，且，则符合条件的一个复数为 　　．
【分析】先设复数，利用复数代数形式的乘除运算化简，求出对应的条件即可．
【解答】解：设复数，则，
，，或，
符合条件的一个复数为，
故答案为：，
【点评】本题考查了复数的代数表示法及代数形式的乘除运算，是基础题．
15．（5分）若，则的值为 　　．
【分析】根据已知条件，先运用三角函数的诱导公式，再结合二倍角公司，即可求解．
【解答】解：，
又，
．
故答案为：．
【点评】本题考查了三角函数的诱导公式，以及二倍角公式，需要学生熟练掌握公式，属于基础题．
16．（5分）已知三棱锥中，平面，，异面直线与所成角的余弦值为，则三棱锥的体积为 　　，三棱锥的外接球的表面积为 　　．
【分析】分别取、、、的中点、、、，连接、、、、，则为异面直线与所成角，可得，设，由余弦定理列式求得，则三棱锥的体积可求；再找出三棱锥的外接球的外心，利用勾股定理求得外接球的半径，代入球的表面积公式得答案．
【解答】解：如图，

分别取、、、的中点、、、，
连接、、、、，
可得，，则为异面直线与所成角，
，
设，可得，，，，则，
在中，由余弦定理，可得，
，解得，
三棱锥的体积为，
设底面三角形的中心为，三棱锥的外接球的球心为，
连接，则平面，
，，
则三棱锥的外接球的半径．
三棱锥的外接球的表面积为．
故答案为：；．
【点评】本题考查空间异面直线所成角，多面体外接球表面积的求法，考查空间想象能力与运算求解能力，是中档题．
四、解答题（本大题共6小题，共计70分．请在答题卡指定区域内作答．解答时应写出文字说明、证明过程或演算步骤）
17．（10分）为了解某市家庭用电量的情况，该市统计局调查了100户居民去年一年的月均用电量，发现他们的用电量都在至之间，进行适当分组后，画出频率分布直方图如图所示
（1）求的值；
（2）为了既满足居民的基本用电需求，又提高能源的利用效率，市政府计划采用阶梯式递增电价（第一档电量满足居民基本用电需求，电价最低；第二档电量反应正常合理用电需求，电价较高；第三档电量体现较高生活质量用电需求，电价最高）定价，希望使不少于的居民缴费在第一档，求第一档月均用电量的最低标准值（单位：．
【分析】（1）由频率分布直方图的性质，可得各个区间的频率和为1，即可求的值．
（2）先分别算出前四组和前五组的频率之和，可确定频率为0.85时对应的数据在第五组，即可求解．
【解答】解：（1）由频率分布直方图的性质，可得，解得．
（2）前四组的频率之和为，
前5组的频率之和为，
频率为0.85时对应的数据在第五组，
第一档月均用电量最低标准值为，
第一档月均用电量的最低标准值．
【点评】本题考查了频率分布直方图的应用问题，也考查了频率、频数与样本容量的应用问题，属于基础题．
18．（12分）如图，四棱柱的底面是正方形，侧面是菱形，，平面平面，，分别为，的中点．
（1）求证：平面；
（2）求与平面所成角的正切值．

【分析】（1）设中点为，则四边形是平行四边形，所以，进而可得到平面；
（2）过作于，则为直线与平面所成的角，再利用几何关系可得与平面所成角的正切值．
【解答】解：（1）证明：设中点为，连接，．
因为，分别为，的中点，
所以，．
在正方形中，是的中点，
所以，且，
所以 且．
所以四边形是平行四边形，
所以．
因为平面，平面，
所以平面．
（2）过作于，过作于，连接，则．
因为平面平面，且平面平面，
平面，所以平面．
所以是在平面的射影．
所以为直线与平面所成的角．
设正方形的边长为，
因为侧面是菱形，，所以．
又因为且是的中点，所以．
在正方形中，为的中点，为的四等分点，．
所以在直角三角形中，．
所以与平面所成角的正弦值为．

【点评】本题考查线面平行的证明，考查线面角的求法，考查直观想象的核心素养，属于中档题．
19．（12分）在条件①；②；③中任选一个，补充在下面的问题中，并求解．
问题：的内角，，所对的边分别为，，，且_____．
（1）求角的大小；
（2）若，求角的大小．
【分析】（1）若选①，由正弦定理，三角形内角和定理，两角和的正弦公式化简已知等式可得，结合范围，可得的值．
若选②，由已知可得，由余弦定理可得，结合范围，可得的值．
若选③，利用两角差的正弦公式，同角三角函数基本关系式化简已知等式可得，结合范围，可得的值．
（2）由题意利用三角函数恒等变换的应用化简已知等式可得，可求范围，，进而解得的值．
【解答】解：（1）若选①，因为，
由正弦定理可得，即，
所以，
因为，
所以可得，
因为，
所以．
若选②，因为，可得，
由余弦定理可得，
因为，
所以．
若选③，因为，
所以，即，，否则不符合题意），
因为，
所以．
（2）因为，所以，即，
又，所以，
原式可化为，化简可得，
因为，，，
所以，或，
解得，或．
【点评】本题主要考查了正弦定理，余弦定理以及三角函数恒等变换在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题．
20．（12分）如图，已知正方形的边长为2，为的中点．
（1）若为的中点，求的值；
（2）若为线段（不含端点）上的一个动点，请探究：当长为多少时，可使得最大？

【分析】（1）直接利用三角函数的值和三角形的边长的关系的应用求出结果；
（2）利用解直角三角形知识的应用和基本不等式的应用求出结果．
【解答】解：设，，，
（1）由于正方形的边长为2，且，分别为，的中点，
所以，
所以，所以．
由于，所以，
所以．
则．
（2）设，其中，
在直角三角形中，，
在直角三角形中，，
所以，
其中：，
令，则，其中，
所以，
由于，
所以，
故，当且仅当时，即时，等号成立，
所以，由于在上单调递增，
当时，可使最大．
【点评】本题考查的知识要点：三角函数的值的应用，基本不等式的应用，主要考查学生的运算能力和数学思维能力，属于中档题．
21．（12分）如图，在中，已知，分别是，的中点，，，与交于点．
（1）若，求的值；
（2）若，求的长．

【分析】（1）有正弦定理可得，，根据，，代入计算即可；
（2）根据条件可得为重心，分别表示出，代入条件可得，再结合大条件求得即．
【解答】解：（1）在中，，，，
由正弦定理可得，所以，
设，，因为为中点，所以，
又因为，
所以；
（2）因为、分别是，的中点，且与交于点，
所以为的重心，所以，
又因为，，
所以，
所以，
因为，，所以，
即，解得舍去），
故．
【点评】本题考查平面向量数量积的运算，正弦定理的应用，以及三角形重心的性质，属于综合中档题．
22．（12分）如图1，在矩形中，已知，，为的中点．将沿向上翻折，进而得到多面体—（如图．

（1）求证：；
（2）在翻折过程中，求二面角的最大值．
【分析】（1）连结交于点，利用三角形相似证明，结合，证明平面，从而证明；
（2）过点作，垂足为，过作，垂足为，连结，利用线面垂直的判定定理和性质定理证明，，从而得到为二面角的平面角，设，则，然后利用三角形的有界性求解最值即可．
【解答】（1）证明：如图1，连结交于点，
因为，且为的中点，则，
在矩形中，因为，，
所以，所以，
所以，
则，即，
由题意可知，，，，，平面，所以平面，
因为平面，所以；
（2）解：如图2，过点作，垂足为，过作，垂足为，连结，
因为平面，平面，所以，
又因为，，，平面，
所以平面，又平面，
所以，
又因为，，，平面，
所以平面，又平面，
所以，
则为二面角的平面角，
在翻折过程中，设，
在矩形中，由，，为的中点，
可得，，
在直角三角形中，，，
所以，
因为，则，
所以，则，
在直角三角形中，，
设，则，
故，所以，
解得，即，
又，所以，
所以二面角的最大值为．

【点评】本题考查了线面垂直的判定定理和性质定理的应用，二面角的求解，解题的关键是利用二面角的平面角定义找到所对应的角，三角函数有界性的应用，考查了逻辑推理能力、空间想象能力与化简运算能力，属于中档题．
声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布
日期：2021/8/23 17:43:49；用户：高中数学12；邮箱：sztdjy76@xyh.com；学号：26722394