2020-2021学年江苏省南京市鼓楼区高一（上）期中数学试卷

2020-2021学年江苏省南京市鼓楼区高一（上）期中数学试卷

一、单项选择题：本大题共8小题，每小题5分，共40分，请把答案直接填写在答题卡相应位置上.

1．（5分）已知集合，2，3，，，4，，则图中阴影部分表示的集合为　　

A．， B．， C．，4， D．，2，3，

2．（5分）命题，的否定为　　

A．， B．不存在， 

C．， D．，

3．（5分）若集合，，则　　

A． B． C． D．

4．（5分）下面各组函数中表示同一个函数的是　　

A．， 

B．， 

C．， 

D．，

5．（5分）已知，，用，表示　　

A． B． C． D．

6．（5分）平流层是指地球表面以上的区域，则在下述不等式中，最适合表示平流层高度的是　　

A． B． C． D．

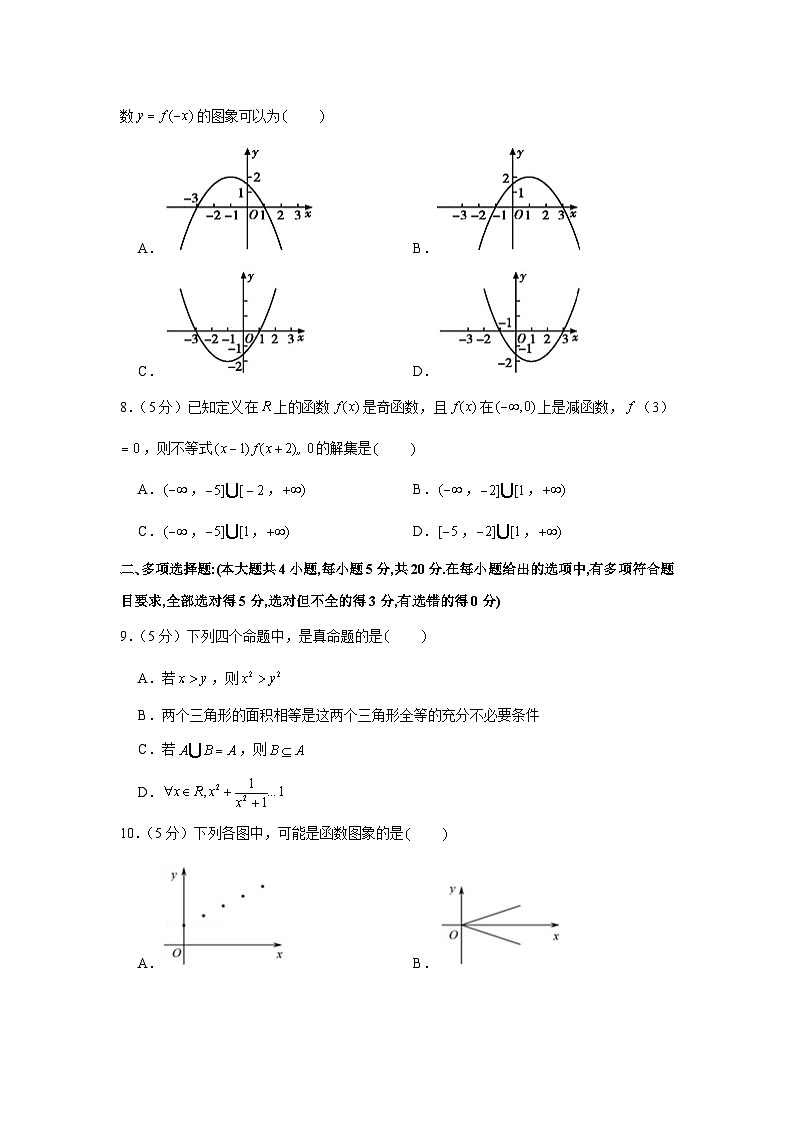
7．（5分）已知函数，不等式的解集为或，则函数的图象可以为　　

A． B． 

C． D．

8．（5分）已知定义在上的函数是奇函数，且在上是减函数，（3），则不等式的解集是　　

A．，， B．，， 

C．，， D．，，

二､多项选择题:(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对得5分,选对但不全的得3分,有选错的得0分)

9．（5分）下列四个命题中，是真命题的是　　

A．若，则 

B．两个三角形的面积相等是这两个三角形全等的充分不必要条件 

C．若，则 

D．

10．（5分）下列各图中，可能是函数图象的是　　

A． B． 

C． D．

11．（5分）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，用其名字命名的“高斯函数”如下：设，用表示不超过的最大整数，则称为高斯函数．例如，，已知函数，若函数的值域集合为，则下列集合是的子集的是　　

A．， B．， C．， D．，2，

12．（5分）已知函数满足：，，且，

则　　

A．（3） B．，（2） 

C． D．若（3），则

三、填空题：本大题共4小题，每小题5分，共20分，请把答案直接填写在答题卡相应位置上.

13．（5分）函数的定义域是　　．

14．（5分）十六、十七世纪之交，随着天文、航海、工程、贸易以及军事的发展，改进数字计算方法成了当务之急，数学家纳皮尔在研究天文学的过程中，为简化计算发明了对数直到十八世纪才由瑞士数学家欧拉发现了指数与对数的互逆关系，即，现在已知，，则　　，　　．（用最简结果作答）

15．（5分）设函数，则　　．

16．（5分）当两个集合中有一个集合为另一集合的子集时称这两个集合之间构成“全食”，当两个集合有公共元素，但互不为对方子集时称两集合之间构成“偏食”．对于集合，，，若与构成“全食”，或构成“偏食”，则的取值集合为　　．

三、解答题：本大题共6小题，共70分，请把答案填写在答题卡相应位置上.

17．（10分）计算；

（1）的值；

（2）已知，，计算的值．

18．（12分）已知，其中为实数．

（1）当时，判断命题，的真假，并说明理由；

（2）若，，，求的取值范围．

19．（12分）中华人民共和国第十四届全运会将于2021年在陕西省举办，全运会会徽以及吉祥物已于2019年8月2日晚在西安市对外发布．某公益团队计划联系全运会组委会举办一场纪念品展销会，并将所获利润全部用于社区体育设施建设．据市场调查，当每套纪念品（一个会徽和一个吉祥物）售价定为元时，销售量可达到万套．为配合这个活动，生产纪念品的厂家将每套纪念品的供货价格分为固定价格和浮动价格两部分，其中固定价格为50元，浮动价格（单位：元）与销售量（单位：万套）成反比，比例系数为10．约定不计其他成本，即销售每套纪念品的利润售价供货价格．

（1）每套会徽及吉祥物售价为100元时，能获得的总利润是多少万元？

（2）每套会徽及吉祥物售价为多少元时，单套的利润最大？最大值是多少元？

20．（12分）（1）已知时，当实数为何值时，是偶函数？

（2）已知是偶函数，且在，是增函数，如果当，时恒成立，求实数的取值范围．

21．（12分）已知函数，其中为实数．

（1）当时，画出函数的图象，并直接写出递增区间；

（2）若在，时的取值范围为，（3），求的取值范围．

22．（12分）已知，．

（1）若关于的方程的解集中恰好有一个元素，求的取值范围；

（2）若，函数在区间，上最大值不超过最小值的2倍，求的取值范围．

2020-2021学年江苏省南京市鼓楼区高一（上）期中数学试卷

参考答案与试题解析

一、单项选择题：本大题共8小题，每小题5分，共40分，请把答案直接填写在答题卡相应位置上.

1．（5分）已知集合，2，3，，，4，，则图中阴影部分表示的集合为　　

A．， B．， C．，4， D．，2，3，

【分析】图中阴影部分表示的集合为，由此能求出阴影部分表示的集合．

【解答】解：集合，2，3，，，4，，

图中阴影部分表示的集合为：

，．

故选：．

【点评】本题考查阴影部分表示的集合的求法，交集定义等基础知识，是基础题．

2．（5分）命题，的否定为　　

A．， B．不存在， 

C．， D．，

【分析】根据含有量词的命题的否定即可得到结论．

【解答】解：命题为全称命题，则命题的否定，，

故选：．

【点评】本题主要考查含有量词的命题的否定，比较基础．

3．（5分）若集合，，则　　

A． B． C． D．

【分析】可以求出集合，然后进行并集的运算即可．

【解答】解：，，

．

故选：．

【点评】本题考查了描述法、区间的定义，一元二次不等式的解法，并集的运算，考查了计算能力，属于基础题．

4．（5分）下面各组函数中表示同一个函数的是　　

A．， 

B．， 

C．， 

D．，

【分析】分别判断两个函数的定义域和对应法则是否相同．

【解答】解：．的定义域为，，两个函数的定义域不相同，不是相同函数．

．，两个函数的定义域，对应法则相同是同一函数．

．，，两个函数的定义域不相同，不是同一函数．

．的定义域为，两个函数的定义域不相同，不是同一函数．

故选：．

【点评】本题主要考查同一函数的判断，结合函数的定义域和对应法则是否相同是解决本题的关键．

5．（5分）已知，，用，表示　　

A． B． C． D．

【分析】利用对数的运算性质求解．

【解答】解：，

故选：．

【点评】本题主要考查了对数的运算性质，是基础题．

6．（5分）平流层是指地球表面以上的区域，则在下述不等式中，最适合表示平流层高度的是　　

A． B． C． D．

【分析】由题意可得，即，即，从而得出结论．

【解答】解：平流层是指地球表面以上到的区域，

若能表示平流层高度，则，所以，

即，

故选：．

【点评】本题主要考查绝对值的意义，绝对值不等式的应用，属于中档题．

7．（5分）已知函数，不等式的解集为或，则函数的图象可以为　　

A． B． 

C． D．

【分析】利用二次函数与不等式的解集，判断开口方向，利用对称性推出所求函数的图象即可．

【解答】解：函数，不等式的解集为或，

所以．并且，1是函数的零点，

函数的图象与函数的图象关于轴对称，所以函数的图象是．

故选：．

【点评】本题考查函数的图象，二次函数的性质的应用，涉及函数的零点，不等式的解法，基本知识的考查．

8．（5分）已知定义在上的函数是奇函数，且在上是减函数，（3），则不等式的解集是　　

A．，， B．，， 

C．，， D．，，

【分析】根据函数奇偶性和单调性之间的关系，即可得到结论．

【解答】解：定义在上的函数是奇函数，且在上是减函数，（3），

在上是减函数，，，

或时，，当或时，，或时，

由可得，或或，

即或，

解得或．

故选：．

【点评】本题主要考查不等式的解法，利用函数的奇偶性和单调性之间的关系是解决本题的关键，综合考查函数性质的应用．

二､多项选择题:(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对得5分,选对但不全的得3分,有选错的得0分)

9．（5分）下列四个命题中，是真命题的是　　

A．若，则 

B．两个三角形的面积相等是这两个三角形全等的充分不必要条件 

C．若，则 

D．

【分析】反例判断；充要条件判断三角形面积与全等关系判断；并集的性质判断；基本不等式判断即可．

【解答】解：对于，若，则，所以是假命题；

对于，两个三角形的面积相等是这两个三角形全等的必要不充分条件，所以是假命题；

对于，若，则，是真命题；

对于，，．当且仅当时，取等号，

所以是真命题．

故选：．

【点评】本题考查命题的真假的判断，考查充要条件，不等式的性质，基本不等式的应用，是基础题．

10．（5分）下列各图中，可能是函数图象的是　　

A． B． 

C． D．

【分析】根据函数的定义，当自变量在定义域内任意取一个值，都有唯一的一个函数值与之对应，由此可得结论．

【解答】解：选项，时有两个值与之对应，不为函数，错误，

其它均符合函数的定义，

故选：．

【点评】本题主要考查函数的定义，函数的图象特征，属于基础题．

11．（5分）高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号，用其名字命名的“高斯函数”如下：设，用表示不超过的最大整数，则称为高斯函数．例如，，已知函数，若函数的值域集合为，则下列集合是的子集的是　　

A．， B．， C．， D．，2，

【分析】根据函数的奇偶性的性质利用新定义求解．

【解答】解：当时：，

即时，的值域是：，，

又是偶函数，的值域是：，，，故正确，错误．

故选：．

【点评】本题考查了函数奇偶性和基本不等式的应用，还考查了对新定义的正确理解，属于中档题．

12．（5分）已知函数满足：，，且，

则　　

A．（3） B．，（2） 

C． D．若（3），则

【分析】求出函数的对称轴，根据函数的对称性和单调性判断各个选项即可．

【解答】解：由，，

则，故函数的图象关于对称，

由，可得在，递减，

结合函数的单调性和对称性得距越近函数值越大，

则显然错误，正确；

对于，故正确；

对于（3）时，距更远，则或，故错误，

故选：．

【点评】本题考查了函数的单调性，对称性问题，考查转化思想，是一道基础题．

三、填空题：本大题共4小题，每小题5分，共20分，请把答案直接填写在答题卡相应位置上.

13．（5分）函数的定义域是　，　．

【分析】根据二次根式的性质求出函数的定义域即可．

【解答】解：由题意，得，解得，

故函数的定义域是，，

故答案为：，．

【点评】本题考查了求函数的定义域问题，考查二次根式的性质，是一道基础题．

14．（5分）十六、十七世纪之交，随着天文、航海、工程、贸易以及军事的发展，改进数字计算方法成了当务之急，数学家纳皮尔在研究天文学的过程中，为简化计算发明了对数直到十八世纪才由瑞士数学家欧拉发现了指数与对数的互逆关系，即，现在已知，，则　8　，　　．（用最简结果作答）

【分析】利用对数恒等式、换底公式即可得出．

【解答】解：，，

则，

．

故答案为：8，．

【点评】本题考查了对数恒等式、换底公式，考查了推理能力与计算能力，属于基础题．

15．（5分）设函数，则　　．

【分析】推导出，从而（2），由此能求出结果．

【解答】解：函数，

，

（2）．

故答案为：．

【点评】本题考查函数值的求法，考查函数性质等基础知识，考查运算求解能力，是基础题．

16．（5分）当两个集合中有一个集合为另一集合的子集时称这两个集合之间构成“全食”，当两个集合有公共元素，但互不为对方子集时称两集合之间构成“偏食”．对于集合，，，若与构成“全食”，或构成“偏食”，则的取值集合为　，，　．

【分析】理解利用新定义和子集的定义．

【解答】解：（1），则，与构成“全食”满足题意，

（2），则，，，此时应构成“偏食”，

或，或，

综上的取值集合为：，，，

故答案为：，，．

【点评】本题考查了对新定义的理解以及子集的概念，分类讨论的思想，容易忽略的情况，但难度不大，属于基础题．

三、解答题：本大题共6小题，共70分，请把答案填写在答题卡相应位置上.

17．（10分）计算；

（1）的值；

（2）已知，，计算的值．

【分析】（1）利用有理数指数幂的运算性质和对数的运算性质求解．

（2）先由得到，把原式化为，代入即可计算出结果．

【解答】解：（1）原式．

（2），，

．

【点评】本题主要考查了有理数指数幂的运算性质和对数的运算性质，是基础题．

18．（12分）已知，其中为实数．

（1）当时，判断命题，的真假，并说明理由；

（2）若，，，求的取值范围．

【分析】（1）直接利用存在性问题的应用求出命题的真假；

（2）利用全称命题的应用和恒成立问题的应用求出参数的取值范围．

【解答】解：（1）该命题为真命题，

当时，，

当时，（2），

则命题，，为真命题；

（2）二次函数关于对称，在上单调递减，在上单调递增，

则当时，的最大值为（1），当时，的最大值为（2），

则对，，恒成立，只需满足，即，

整理得：，即．

故的取值范围为．

【点评】本题考查的知识要点：命题真假的判定，特称命题，二次函数性质的应用，恒成立问题和全称命题的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题．

19．（12分）中华人民共和国第十四届全运会将于2021年在陕西省举办，全运会会徽以及吉祥物已于2019年8月2日晚在西安市对外发布．某公益团队计划联系全运会组委会举办一场纪念品展销会，并将所获利润全部用于社区体育设施建设．据市场调查，当每套纪念品（一个会徽和一个吉祥物）售价定为元时，销售量可达到万套．为配合这个活动，生产纪念品的厂家将每套纪念品的供货价格分为固定价格和浮动价格两部分，其中固定价格为50元，浮动价格（单位：元）与销售量（单位：万套）成反比，比例系数为10．约定不计其他成本，即销售每套纪念品的利润售价供货价格．

（1）每套会徽及吉祥物售价为100元时，能获得的总利润是多少万元？

（2）每套会徽及吉祥物售价为多少元时，单套的利润最大？最大值是多少元？

【分析】（1）先求出每套会徽及吉祥物售价为100元时的销售量，再求出供货单价，即可求出总利润．

（2）由题意可知销售量为，供货单价为，从而求出单套利润为，再利用基本不等式即可求出单套利润的最大值．

【解答】解：（1）每套会徽及吉祥物售价为100元时，销售量为（万套），

供货单价为（元，

总利润为（万元），

答：总利润为240万元．

（2）销售量为，供货单价为，

单套利润为，因为，所以，

所以单套利润为，当且仅当即时，等号成立，

所以每套会徽及吉祥物售价为140元时，单套的利润最大，最大值是80元．

【点评】本题主要考查了函数的实际应用，考查了利用基本不等式求最值，是中档题．

20．（12分）（1）已知时，当实数为何值时，是偶函数？

（2）已知是偶函数，且在，是增函数，如果当，时恒成立，求实数的取值范围．

【分析】（1）由已知及偶函数的定义代入可求，

（2）结合偶函数的定义及单调性即可求解不等式，可求．

【解答】解：（1）当时，是偶函数，

当，，而（a），此时不可能是偶函数，

所以，

（2）由为偶函数可知，且，，

由在，上单调递增及可知时，恒成立，

即时，恒成立，

故，

所以．

【点评】本题主要考查了函数奇偶性的判断及利用函数单调性及奇偶性解不等式，属于函数性质的综合应用．

21．（12分）已知函数，其中为实数．

（1）当时，画出函数的图象，并直接写出递增区间；

（2）若在，时的取值范围为，（3），求的取值范围．

【分析】（1）当时，，画图即可，并由图象可得函数的单调区间，

（2）先求出方程的根，再分类讨论，根据函数单调性，即可求出的范围．

【解答】解：（1）当时，，

函数递增区间为和；

（2）解方程，可得或，结合条件可知，，

①当时，符合题意，

②当时，不符合题意．

③当，，

在，上单调递减，在，上单调的递增，

值需要（3）（1），解得，

所以；

④当时，，

在，单调递增，在，上单调递减，在，上单调递增，

显然（1）（a），

所以只需要（3），解得，

所以，

综上所述的取值范围为，．

【点评】本题考查了解绝对值不等式问题，考查分类讨论思想，是一道中档题．

22．（12分）已知，．

（1）若关于的方程的解集中恰好有一个元素，求的取值范围；

（2）若，函数在区间，上最大值不超过最小值的2倍，求的取值范围．

【分析】（1）化简方程，根据二次方程的性质求解即可；

（2）先求出函数的最大值和最小值，然后根据已知最值的关系建立不等式，整理化简建立新函数，求出新函数的单调性，利用恒成立思想即可求解．

【解答】解：（1）方程，即方程，其中，

整理可得：，

显然不是方程的根，

所以方程在上只有一解，

当即时，符合题意，

当即时，△，解得，

所以，；

（2）因为函数在是单调递减，而任意，，，

所以函数在，上单调递减，

所以在，上，的最大值为，最小值为，

由题意可得：任意，恒成立，

即任意，，恒成立，下面来说明的单调性，

任意，，，且，则

，

因为，所以，，，

所以，即在，上单调递减，

所以只需的最大值即，

解得，

故的取值范围为，．

【点评】本题考查了函数的最值问题以及恒成立问题，涉及到函数的单调性以及一元二次方程根的情况，考查了学生的运算能力，属于中档题．

声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布

日期：2021/2/23 14:17:23；用户：高中数学12；邮箱：sztdjy76@xyh.com；学号：26722394