2022-2023学年陕西省西安市高新一中九年级（上）开学数学试卷

这是一份2022-2023学年陕西省西安市高新一中九年级（上）开学数学试卷，共16页。试卷主要包含了选择题等内容，欢迎下载使用。

2022-2023学年陕西省西安市高新一中九年级（上）开学数学试卷
一、选择题（本大题共8小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．（3分）下列方程属于一元二次方程的是（　　）
A．xy＝6 B．x+y＝5 C．x2+2x＝0 D．x+＝5
2．（3分）下面各式从左到右的变形，属于因式分解的是（　　）
A．x2﹣x﹣1＝x（x﹣1）﹣1 B．x2﹣1＝（x﹣1）2
C．x2﹣x﹣6＝（x﹣3）（x+2） D．x（x﹣1）＝x2﹣x
3．（3分）如图，▱ABCD对角线AC，BD交于点O，请添加一个条件：____使得▱ABCD是菱形（　　）

A．AB＝AC B．AC⊥BD C．AB＝CD D．AC＝BD
4．（3分）用配方法解方程x2﹣6x+5＝0，配方后可得（　　）
A．（x﹣3）2＝5 B．（x﹣3）2＝4 C．（x﹣6）2＝5 D．（x﹣6）2＝31
5．（3分）如图，在▱ABCD中，点E、H、F、G分别在边AB、BC、CD、DA上，EF∥AD，GH∥CD，EF与GH交于点O，则图中的平行四边形一共有（　　）

A．6个 B．7个 C．8个 D．9个
6．（3分）把分式中的x和y都扩大2倍，分式的值（　　）
A．不变 B．扩大2倍 C．缩小2倍 D．扩大4倍
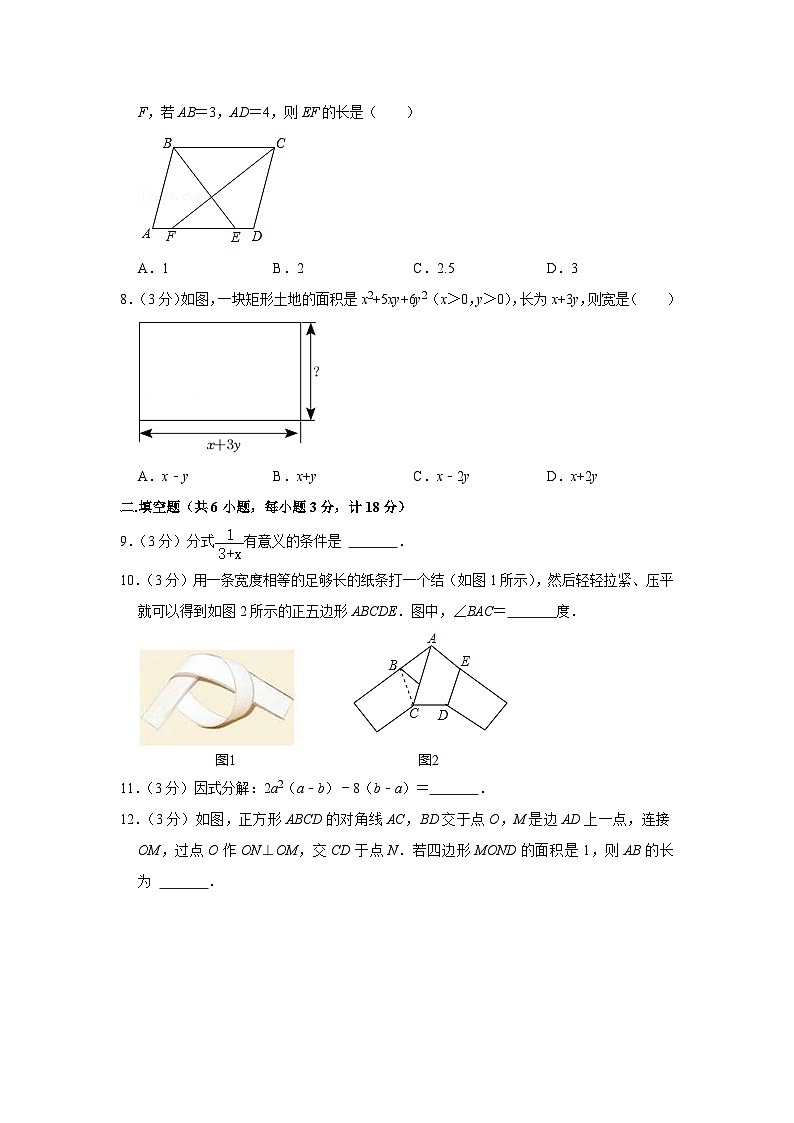
7．（3分）如图，在▱ABCD中，∠ABC的平分线交AD于点E，∠BCD的平分线交AD于点F，若AB＝3，AD＝4，则EF的长是（　　）

A．1 B．2 C．2.5 D．3
8．（3分）如图，一块矩形土地的面积是x2+5xy+6y2（x＞0，y＞0），长为x+3y，则宽是（　　）

A．x﹣y B．x+y C．x﹣2y D．x+2y
二.填空题（共6小题，每小题3分，计18分）
9．（3分）分式有意义的条件是 　 　．
10．（3分）用一条宽度相等的足够长的纸条打一个结（如图1所示），然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE．图中，∠BAC＝　 　度．

11．（3分）因式分解：2a2（a﹣b）﹣8（b﹣a）＝　 　．
12．（3分）如图，正方形ABCD的对角线AC，BD交于点O，M是边AD上一点，连接OM，过点O作ON⊥OM，交CD于点N．若四边形MOND的面积是1，则AB的长为 　 　．

13．（3分）若关于x的一元二次方程x2+x+m＝0有两个相等的实数根，则m＝　 　．
14．（3分）如图，在矩形ABCD中，AB＝3，AD＝，点P在AD上，点Q在BC上，且AP＝CQ，连接CP，QD，则PC+QD的最小值为 　 　．

三.解答题（共6小题，计58分.解答应写出过程）
15．（5分）先化简，再求值：，其中a＝1．
16．（15分）解方程：
（1）+2；
（2）2x2+4x＝x+2；
（3）x2﹣2x﹣1＝0．
17．（7分）如图，已知平面直角坐标系和线段a，b．请用尺规作图法，求作▱ABCD，使∠ABC＝45°，AB＝a，BC＝b．（不写作法，保留作图痕迹）


18．（9分）为了让学生崇尚劳动，尊重劳动，在劳动中提升综合素质，某校定期开展劳动实践活动．甲、乙两班在一次体验挖土豆的活动中，甲班挖1500千克土豆与乙班挖1200千克土豆所用的时间相同．已知甲班平均每小时比乙班多挖100千克土豆，问乙班平均每小时挖多少千克土豆？
19．（10分）如图，在矩形ABCD中，E，F是AB和CD上的两点，且AE＝CF，连接EF，BF，EF与对角线AC交于点O，且BE＝BF，∠BEF＝2∠BAC．
（1）求证：四边形AECF是平行四边形；
（2）若BC＝2，求AB的长．

20．（12分）我们给出如下定义：顺次连接任意一个四边形各边中所得的四边形叫中点四边形．

（1）如图1，在四边形ABCD中，点E、F、G、H分别为边AB、BC、CD、DA的中点，求证：中点四边形EFGH是平行四边形．
（2）如图2，点P是四边形ABCD内一点，且满足PA＝PB，PC＝PD，∠APB＝∠CPD，点E、F、G、H分别为边AB、BC、CD、DA的中点．猜想中点四边形EFGH的形状，并证明你的猜想．
（3）若改变（2）中的条件，使∠APB＝∠CPD＝90°，其他条件不变，直接写出中点四边形EFGH的形状（不必证明）．

2022-2023学年陕西省西安市高新一中九年级（上）开学数学试卷
参考答案与试题解析
一、选择题（本大题共8小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1．（3分）下列方程属于一元二次方程的是（　　）
A．xy＝6 B．x+y＝5 C．x2+2x＝0 D．x+＝5
【解答】解：A、方程中含有两个未知数，不是一元二次方程，故该选项不符合题意；
B、方程中含有两个未知数，不是一元二次方程，故该选项不符合题意；
C、只含有1个未知数，未知数的最高次数是2，故该选项符合题意；
D、该方程不是整式方程，故该选项不符合题意；
故选：C．
2．（3分）下面各式从左到右的变形，属于因式分解的是（　　）
A．x2﹣x﹣1＝x（x﹣1）﹣1 B．x2﹣1＝（x﹣1）2
C．x2﹣x﹣6＝（x﹣3）（x+2） D．x（x﹣1）＝x2﹣x
【解答】解：A选项不是因式分解，故不符合题意；
B选项计算错误，故不符合题意；
C选项是因式分解，故符合题意；
D选项不是因式分解，故不符合题意；
故选：C．
3．（3分）如图，▱ABCD对角线AC，BD交于点O，请添加一个条件：____使得▱ABCD是菱形（　　）

A．AB＝AC B．AC⊥BD C．AB＝CD D．AC＝BD
【解答】解：当AC⊥BD时，▱ABCD是菱形，
故选：B．
4．（3分）用配方法解方程x2﹣6x+5＝0，配方后可得（　　）
A．（x﹣3）2＝5 B．（x﹣3）2＝4 C．（x﹣6）2＝5 D．（x﹣6）2＝31
【解答】解：x2﹣6x+5＝0，
x2﹣6x＝﹣5，
x2﹣6x+9＝﹣5+9，
（x﹣3）2＝4，
故选：B．
5．（3分）如图，在▱ABCD中，点E、H、F、G分别在边AB、BC、CD、DA上，EF∥AD，GH∥CD，EF与GH交于点O，则图中的平行四边形一共有（　　）

A．6个 B．7个 C．8个 D．9个
【解答】解：∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，
∵AD∥EF，CD∥GH，
∴AB∥GH∥CD，AD∥EF∥BC，
∴平行四边形有：▱ABCD，▱ABHG，▱CDGH，▱BCFE，▱ADFE，▱AGOE，▱BEOH，▱OFCH，▱OGDF共9个．
即共有9个平行四边形．
故选：D．
6．（3分）把分式中的x和y都扩大2倍，分式的值（　　）
A．不变 B．扩大2倍 C．缩小2倍 D．扩大4倍
【解答】解：分式中的x和y都扩大2倍，则原分式变形为：＝＝2•，
所以把分式中的x和y都扩大2倍，分式的值扩大2倍．
故选：B．
7．（3分）如图，在▱ABCD中，∠ABC的平分线交AD于点E，∠BCD的平分线交AD于点F，若AB＝3，AD＝4，则EF的长是（　　）

A．1 B．2 C．2.5 D．3
【解答】解：∵四边形ABCD是平行四边形，
∴AD∥CB，AB＝CD＝3，AD＝BC＝4，
∴∠DFC＝∠FCB，
又∵CF平分∠BCD，
∴∠DCF＝∠FCB，
∴∠DFC＝∠DCF，
∴DF＝DC＝3，
同理可证：AE＝AB＝3，
∴AF＝DE
∵AD＝4，
∴AF＝4﹣3＝1，
∴EF＝4﹣1﹣1＝2．
故选：B．
8．（3分）如图，一块矩形土地的面积是x2+5xy+6y2（x＞0，y＞0），长为x+3y，则宽是（　　）

A．x﹣y B．x+y C．x﹣2y D．x+2y
【解答】解：∵x2+5xy+6y2＝（x+2y）（x+3y），
又∵一块矩形土地的面积是x2+5xy+6y2（x＞0，y＞0），长为x+3y，
∴宽为x+2y，
故选：D．
二.填空题（共6小题，每小题3分，计18分）
9．（3分）分式有意义的条件是 　x≠﹣3　．
【解答】解：根据题意得：3+x≠0，
∴x≠﹣3．
故答案为：x≠﹣3．
10．（3分）用一条宽度相等的足够长的纸条打一个结（如图1所示），然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE．图中，∠BAC＝　36　度．

【解答】解：∵∠ABC＝＝108°，△ABC是等腰三角形，
∴∠BAC＝∠BCA＝36度．
11．（3分）因式分解：2a2（a﹣b）﹣8（b﹣a）＝　2（a﹣b）（a2+4）　．
【解答】解：2a2（a﹣b）﹣8（b﹣a）＝2（a﹣b）（a2+4）．
故答案为：2（a﹣b）（a2+4）．
12．（3分）如图，正方形ABCD的对角线AC，BD交于点O，M是边AD上一点，连接OM，过点O作ON⊥OM，交CD于点N．若四边形MOND的面积是1，则AB的长为 　2　．

【解答】解：∵四边形ABCD是正方形，
∴∠MDO＝∠NCO＝45°，OD＝OC，∠DOC＝90°，
∴∠DON+∠CON＝90°，
∵ON⊥OM，
∴∠MON＝90°，
∴∠DON+∠DOM＝90°，
∴∠DOM＝∠CON，
在△DOM和△CON中，
，
∴△DOM≌△CON（ASA），
∵四边形MOND的面积是1，四边形MOND的面积＝△DOM的面积+△DON的面积，
∴四边形MOND的面积＝△CON的面积+△DON的面积＝△DOC的面积，
∴△DOC的面积是1，
∴正方形ABCD的面积是4，
∴AB2＝4，
∴AB＝2，
故答案为：2．
13．（3分）若关于x的一元二次方程x2+x+m＝0有两个相等的实数根，则m＝　　．
【解答】解：根据题意得Δ＝12﹣4m＝0，
解得m＝．
故答案为．
14．（3分）如图，在矩形ABCD中，AB＝3，AD＝，点P在AD上，点Q在BC上，且AP＝CQ，连接CP，QD，则PC+QD的最小值为 　　．

【解答】解：如图，连接BP，

在矩形ABCD中，AD∥BC，AD＝BC，
∵AP＝CQ，
∴AD﹣AP＝BC﹣CQ，
∴DP＝QB，DP∥BQ，
∴四边形DPBQ是平行四边形，
∴PB∥DQ，PB＝DQ，
则PC+QD＝PC+PB，则PC+QD的最小值转化为PC+PB的最小值，
在BA的延长线上截取AE＝AB＝3，连接PE，
∵PA⊥BE，
∴PA是BE的垂直平分线，
∴PB＝PE，
∴PC+PB＝PC+PE，
连接CE，则PC+QD＝PC+PB＝PC+PE≥CE，
∵BE＝2AB＝6，BC＝AD＝，
∴CE＝＝．
∴PC+PB的最小值为．
故答案为：．
三.解答题（共6小题，计58分.解答应写出过程）
15．（5分）先化简，再求值：，其中a＝1．
【解答】解：
＝÷
＝
＝，
当a＝1时，原式＝＝．
16．（15分）解方程：
（1）+2；
（2）2x2+4x＝x+2；
（3）x2﹣2x﹣1＝0．
【解答】解：（1）去分母得：﹣2＝1﹣x+2（x﹣4），
解得：x＝5，
检验：把x＝5代入得：x﹣4＝1≠0，
∴分式方程的解为x＝5；

（2）2x2+4x＝x+2
2x2+3x﹣2＝0，
∴a＝2，b＝3，c＝﹣2，
则Δ＝32﹣4×2×（﹣2）＝25＞0，
∴x＝＝，
∴x1＝﹣2，x2＝；

（3）x2﹣2x﹣1＝0，
x2﹣2x＝1，
（x﹣1）2＝2，
x﹣1＝±，
∴x1＝1+，x2＝1﹣．
17．（7分）如图，已知平面直角坐标系和线段a，b．请用尺规作图法，求作▱ABCD，使∠ABC＝45°，AB＝a，BC＝b．（不写作法，保留作图痕迹）


【解答】解：如图，▱ABCD为所作．

18．（9分）为了让学生崇尚劳动，尊重劳动，在劳动中提升综合素质，某校定期开展劳动实践活动．甲、乙两班在一次体验挖土豆的活动中，甲班挖1500千克土豆与乙班挖1200千克土豆所用的时间相同．已知甲班平均每小时比乙班多挖100千克土豆，问乙班平均每小时挖多少千克土豆？
【解答】解：设乙班平均每小时挖x千克土豆，
根据题意，得，
解得x＝400，
经检验，x＝400是原方程的根，且符合题意；
答：乙班平均每小时挖400千克土豆．
19．（10分）如图，在矩形ABCD中，E，F是AB和CD上的两点，且AE＝CF，连接EF，BF，EF与对角线AC交于点O，且BE＝BF，∠BEF＝2∠BAC．
（1）求证：四边形AECF是平行四边形；
（2）若BC＝2，求AB的长．

【解答】（1）证明：在矩形ABCD中，AB∥CD，
∴AE∥CF，
又∵AE＝CF，
∴四边形AECF是平行四边形；
（2）解：如图，连接OB，

在矩形ABCD中，AB∥CD，
∴∠BAC＝∠FCO，
在△AOE和△COF中，
，
∴△AOE≌△COF（AAS），
∴OE＝OF；
∵BE＝BF，OE＝OF，
∴BO⊥EF，
在Rt△BEO中，∠BEF+∠ABO＝90°，
由直角三角形斜边上的中线等于斜边上的一半可知：OA＝OB＝OC，
∴∠BAC＝∠ABO，
又∵∠BEF＝2∠BAC，
即2∠BAC+∠BAC＝90°，
解得∠BAC＝30°，
∵BC＝2，
∴AC＝2BC＝4，
∴AB＝＝＝2．
即AB的长为2．
20．（12分）我们给出如下定义：顺次连接任意一个四边形各边中所得的四边形叫中点四边形．

（1）如图1，在四边形ABCD中，点E、F、G、H分别为边AB、BC、CD、DA的中点，求证：中点四边形EFGH是平行四边形．
（2）如图2，点P是四边形ABCD内一点，且满足PA＝PB，PC＝PD，∠APB＝∠CPD，点E、F、G、H分别为边AB、BC、CD、DA的中点．猜想中点四边形EFGH的形状，并证明你的猜想．
（3）若改变（2）中的条件，使∠APB＝∠CPD＝90°，其他条件不变，直接写出中点四边形EFGH的形状（不必证明）．
【解答】（1）证明：如图1中，连接BD．
∵点E，H分别为边AB，DA的中点，
∴EH∥BD，EH＝BD，
∵点F，G分别为边BC，CD的中点，
∴FG∥BD，FG＝BD，
∴EH∥FG，EH＝GF，
∴中点四边形EFGH是平行四边形．

（2）解：结论：四边形EFGH是菱形．
理由：如图2中，连接AC，BD．
∵∠APB＝∠CPD，
∴∠APB+∠APD＝∠CPD+∠APD
即∠APC＝∠BPD，
在△APC和△BPD中，
，
∴△APC≌△BPD（SAS），
∴AC＝BD
∵点E，F，G分别为边AB，BC，CD的中点，
∴EF＝AC，FG＝BD，
∵四边形EFGH是平行四边形，
∴四边形EFGH是菱形．

（3）解：结论：四边形EFGH是正方形．
理由：如图2中，设AC与BD交于点O．AC与PD交于点M，AC与EH交于点N．
∵△APC≌△BPD，
∴∠ACP＝∠BDP，
∵∠DMO＝∠CMP，
∴∠COD＝∠CPD＝90°，
∵EH∥BD，AC∥HG，
∴∠EHG＝∠ENO＝∠BOC＝∠DOC＝90°，
∵四边形EFGH是菱形，
∴四边形EFGH是正方形．


声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2022/9/15 7:47:52；用户：fly；邮箱：orFmNt8V1e4zijZdHFWnbKrn1ehk@weixin.jyeoo.com；学号：38459288

菁优网APP 菁优网公众号 菁优网小程序