还剩20页未读,
继续阅读
2023年河南省洛阳市孟津县中考数学一模试卷(含解析)
展开
这是一份2023年河南省洛阳市孟津县中考数学一模试卷(含解析),共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列各数中,最小的有理数是( )
A. −2023B. 0C. 12023D. −2022
2. 如图所示的几何体的主视图是( )
A.
B.
C.
D.
3. 已知显微镜下肆虐横行的被人们称为“大毒王”的新冠病毒变异毒株奥密克戎直径约为0.0000001米,该长度用科学记数法表示为( )
A. 10×106米B. 10−6米C. 10−7米D. 0.1×10−6米
4. 如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
A. 30°B. 50°C. 120°D. 140°
5. 下列运算正确的是( )
A. a2+a2=2a4B. 3a2−2a3=6a6
C. (−2ab3)2=4a2b6D. a6÷a2=a3
6. 不等式组3x<2x+12x+5≥−1的解集在数轴上表示正确的是( )
A. B.
C. D.
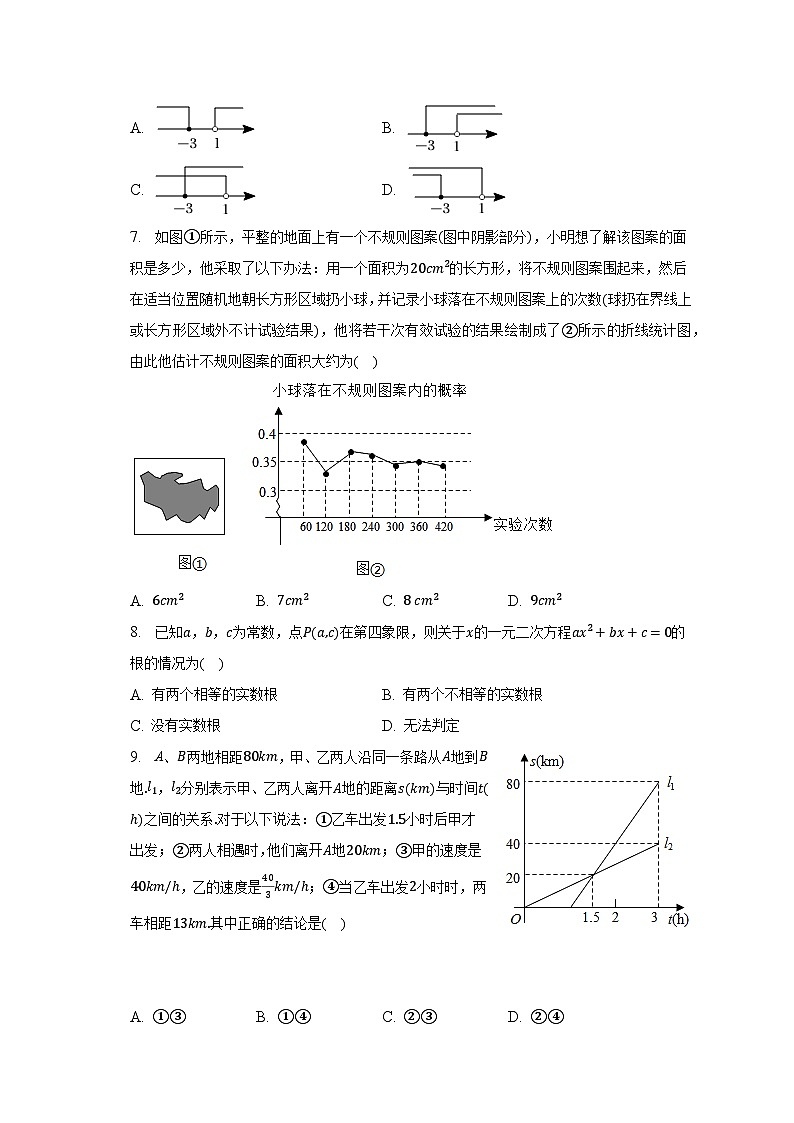
7. 如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个面积为20cm2的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A. 6cm2B. 7cm2C. 8 cm2D. 9cm2
8. 已知a,b,c为常数,点P(a,c)在第四象限,则关于x的一元二次方程ax2+bx+c=0的根的情况为( )
A. 有两个相等的实数根B. 有两个不相等的实数根
C. 没有实数根D. 无法判定
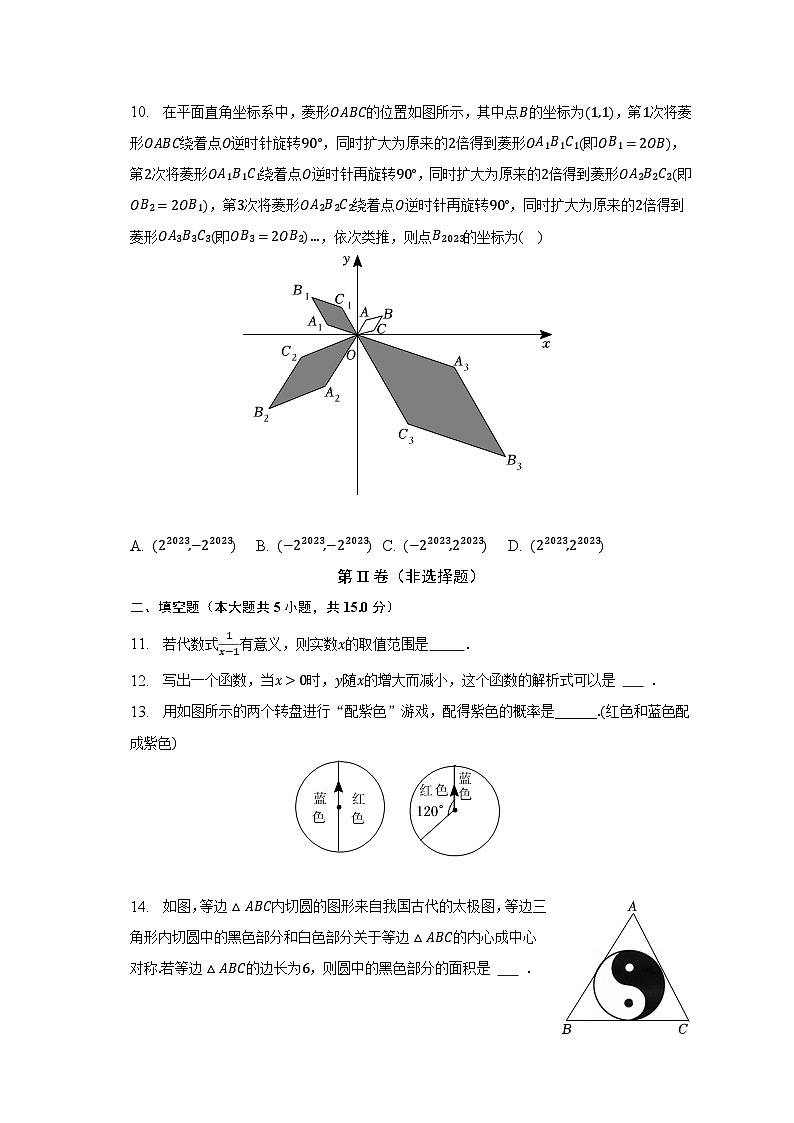
9. A、B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是403km/h;④当乙车出发2小时时,两车相距13km.其中正确的结论是( )
A. ①③B. ①④C. ②③D. ②④
10. 在平面直角坐标系中,菱形OABC的位置如图所示,其中点B的坐标为(1,1),第1次将菱形OABC绕着点O逆时针旋转90°,同时扩大为原来的2倍得到菱形OA1B1C1(即OB1=2OB),第2次将菱形OA1B1C1绕着点O逆时针再旋转90°,同时扩大为原来的2倍得到菱形OA2B2C2(即OB2=2OB1),第3次将菱形OA2B2C2绕着点O逆时针再旋转90°,同时扩大为原来的2倍得到菱形OA3B3C3(即OB3=2OB2)…,依次类推,则点B2023的坐标为( )
A. (22023,−22023)B. (−22023,−22023)C. (−22023,22023)D. (22023,22023)
第II卷(非选择题)
二、填空题(本大题共5小题,共15.0分)
11. 若代数式1x−1有意义,则实数x的取值范围是 .
12. 写出一个函数,当x>0时,y随x的增大而减小,这个函数的解析式可以是 .
13. 用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是______.(红色和蓝色配成紫色)
14. 如图,等边△ABC内切圆的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称.若等边△ABC的边长为6,则圆中的黑色部分的面积是 .
15. 如图,直角三角形纸片ABC中,∠ABC=90°,AB=6,BC=8.点D为AC的中点,点E为BC一动点(不与端点重合),且CE<4,沿直线DE折叠该纸片,点C的对应点为C1,再沿直线BC折叠该纸片,点C的对应点为C2,设点C2,D之间的距离为d,则d的取值范围为______ .
三、解答题(本大题共8小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)
16. (本小题10.0分)
(1)计算:(π−1)0−2sin60°+ 3−|−3|;
(2)化简:(x2+1x−2)÷x2−1x.
17. (本小题9.0分)
甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,根据两个班选手的进球数,制作了如下统计图及数据分析表.
(1)写出表格中a,b,c的值:a= ______ ,b= ______ ,c= ______ ;
(2)如果要从这两个班中选出一个班参加学校的投篮比赛,你认为应该选择哪个班比较合适?为什么?
18. (本小题9.0分)
西安市某校为进一步预防“新型冠状病毒”,对全校所有的教室都进行了“熏药法消毒”处理,已知该药物在燃烧释放过程中,教室内空气中每立方米的含药量y(mg)与燃烧时间x(min)之间的函数关系如图所示,其中当x<6时,y是x的正比例函数,当x≥6时,y是x的反比例函数,根据图象提供的信息,解答下列问题:
(1)求当x≥6时,y与x的函数关系式;
(2)药物燃烧释放过程中,若空气中每立方米的含药量不小于1.5mg的时间超过30分钟,即为有效消毒,请问本题中的消毒是否为有效消毒?
19. (本小题9.0分)
图1是电脑及电脑支架实物图,图2是其示意图,DG是电脑屏幕,托杠AB=BC=CD=24cm,支杠MN=EF=10cm,B,M,F为固定点,BF=10cm,支杠MN,EF可分别绕着点M,F旋转,点E,N分别在AB,BC上滑动.当电脑及电脑支架按如图所示的方式放置时,AE=6cm.
(1)求∠B的度数.
(2)当FN=3cm,MN⊥CD时,试通过计算说明点D是否位于点B的正上方.(参考数据:sin36°≈0.59,cs26°≈0.90,sin18°≈0.31)
20. (本小题9.0分)
近两年,共享经济快速崛起,共享汽车、共享单车、共享雨伞、共享KTV、共享充电宝等等.现南宁市计划在城区再投放一批“共享新能源汽车”,这批汽车分为A,B两种不同款型,其中A型车单价5万元,B型车单价3万元.
(1)今年年初,“共享新能源汽车”再投放在城区正式启动,投放A,B两种款型的汽车共80辆,总价值340万元.试问本次试点投放的A型车与B型车各多少辆?
(2)为鼓励市民绿色出行,特推出以下优惠活动:
①优惠卡:保证金2500元(还车可退回),每小时内(含1小时)18元;
②VIP卡:会员费1680元(不退还),每小时内(含1小时)12元.
若市民出行每次用车均不超过1小时,如何选择才能使一年内租用共享汽车最合算.
21. (本小题9.0分)
如图,四边形ABCD内接于⊙O,AB是直径,点D是AC的中点.
(1)求证:OD//BC;
(2)连接AC交OD于点E,若AC=8,DE=2,求⊙O的半径.
22. (本小题10.0分)
燃放烟花是一种常见的喜庆活动.如图,小杰燃放一种手持烟花,这种烟花每隔2s发射一枚花弹,每枚花弹的飞行路径视为同一条抛物线,飞行相同时间后发生爆炸,小杰发射出的第一枚花弹的飞行高度h(单位:m)随飞行时间(单位:s)变化的规律如表:
(1)求第一枚花弹的飞行高度h与飞行时间t的函数解析式;(不要求写出自变量的取值范围)
(2)为了安全,要求花弹爆炸时的高度不低于30m.小杰发现在第一枚花弹爆炸的同时,第二枚花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求.
23. (本小题10.0分)
在等边三角形ABC中,点D是线段BC上一点,点E是直线AB上一动点,连接DE,把射线DE绕点D顺时针旋转120°,与直线AC相交于点F.
(1)若点D为线段BC中点.
①如图1,当点E在线段AB上,且DE⊥AB时,请直接写出线段DE与DF的数量关系:______ ;
②如图2,当点E落在线段AB上,点F落在射线AC上时,①中的结论是否仍然成立?请结合图2说明理由;
(2)如图3,若点D为边BC上靠近点G的三等分点.当AE:BE=3:2时,直接写出CFAF的值.
答案和解析
1.【答案】A
【解析】解:∵−2023<−2022<0<12023,
∴最小的有理数是−2023,
故选:A.
根据正数都大于0,负数都小于0,正数大于负数,两个负数,绝对值大的反而小;进行比较,即可求解.
本题考查了有理数的大小比较,熟练掌握有理数大小比较的方法是解答本题的关键.
2.【答案】D
【解析】解:从正面看,是一个等腰三角形.
故选:D.
根据从正面看得到的图形是主视图,可得答案.
本题考查了简单组合体的三视图,从正面看得到的图形是主视图.
3.【答案】C
【解析】解:0.0000001米=10−7米.
故选:C.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
本题考查了科学记数法表示绝对值较大的数的方法,掌握科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数是关键.
4.【答案】D
【解析】解:∵∠BOD=50°,
∴∠AOC=50°,
∵EO⊥AB,
∴∠COE=90°+50°=140°.
故选:D.
利用对顶角的定义结合垂线的定义得出∠COE=90°+50°求出即可.
此题主要考查了对顶角以及垂线的定义,得出∠AOC度数是解题关键.
5.【答案】C
【解析】解:A、∵a2+a2=2a2,∴本选项错误.
B、∵3a2和2a3不是同类项,∴本选项错误.
C、∵(−2ab3)2=4a2b6,∴本选项正确.
D、∵a6÷a2=a4,∴本选项错误.
故选:C.
利用合并同类项法则,单项式乘单项式,积的乘方性质同底数幂乘除法判断即可.
本题主要考查合并同类项,单项式乘单项式,积的乘方运算与幂的乘方运算,同底数幂的运算,掌握运算法则是解决此题的关键.
6.【答案】C
【解析】解:3x<2x+1①2x+5≥−1②,
解不等式①得:x<1,
解不等式②得:x≥−3,
∴原不等式组的解集为:−3≤x<1,
∴该不等式组的解集在数轴上表示如图所示:
故选:C.
按照解一元一次不等式组的步骤,进行计算即可解答.
本题考查了解一元一次不等式组,在数轴上表示不等式的解集,熟练掌握解一元一次不等式组是解题的关键.
7.【答案】B
【解析】
【分析】
本题分两部分求解,首先设不规则图案的面积为xcm2,根据几何概率知识求解不规则图案占长方形的面积大小,继而根据折线图用频率估算概率,综合以上列方程求解即可.
本题考查几何概率以及用频率估计概率,并在此基础上进行题目创新,解题的关键在于理解题意,能从复杂的题目背景中找到考点化繁为简.
【解答】解:假设不规则图案的面积为xcm2,
由已知得:长方形面积为20cm2,
根据几何概率公式小球落在不规则图案的概率为:x20,
当事件A试验次数足够多,即样本足够大时,其频率可作为事件A发生的概率估计值,故由折线图可知,小球落在不规则图案的概率大约为0.35,
综上:x20=0.35,
解得:x=7,
∴不规则图案的面积大约为7cm2,
故选:B.
8.【答案】B
【解析】解:∵点P(a,c)在第四象限,
∴a>0,c<0,
∴ac<0,
∴方程ax2+bx+c=0的判别式Δ=b2−4ac>0,
∴方程ax2+bx+c=0有两个不相等的实数根.
故选:B.
先利用第二象限点的坐标特征得到ac<0,则判断Δ>0,然后根据判别式的意义判断方程根的情况.
本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.
9.【答案】C
【解析】解:由图可得,
乙车出发1.5小时后甲已经出发一段时间,故①错误;
两人相遇时,他们离开A地20km,故②正确;
甲的速度是(80−20)÷(3−1.5)=40(km/h),乙的速度是40÷3=403(km/h),故③正确;
当乙车出发2小时时,两车相距:[20+40×(2−1.5)]−403×2=403(km),故④错误;
故选:C.
根据题意和函数图象中的数据,可以判断各个小题中的结论是否正确,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
10.【答案】A
【解析】解:∵点B的坐标为(1,1),第1次将菱形OABC绕着点O逆时针旋转90°,同时扩大为原来的2倍得到菱形OA1B1C1(即OB1=2OB),
∴B1的坐标为(−2,2),
同理:B2的坐标为(−4,−4),即(−22,−22),
B3的坐标为(8,−8),即(23,−23),
B4的坐标为(16,16),即(24,24),
……,
∵2023÷4=505……3,
∴点B2023的坐标为(22023,−22023),
故选:A.
由题意得B1的坐标为(−2,2),同理B2的坐标为(−4,−4),即(−22,−22),B3的坐标为(8,−8),即(23,−23),B4的坐标为(16,16),即(24,24),……,
再由2023÷4=505……3,即可得出结论.
本题考查了菱形的性质、坐标与图形性质以及规律型等知识,找出点Bn的坐标规律是解题的关键.
11.【答案】x≠1
【解析】
【分析】
本题考查了分式有意义的条件,分式有意义的条件是分母不等于零.
分式有意义时,分母x−1≠0,据此求得x的取值范围即可.
【解答】
解:依题意得:x−1≠0,
解得x≠1,
故答案为:x≠1.
12.【答案】y=−2x(x>0),答案不唯一
【解析】解:只要使反比例系数大于0即可.如y=−2x(x>0),答案不唯一.
故答案为:y=−2x(x>0),答案不唯一.
反比例函数的图象在每个象限内,函数值y随自变量x的增大而减小,则反比例函数的反比例系数k<0.
本题主要考查了反比例函数y=kx(k≠0)的性质:①k>0时,函数图象在第一,三象限.在每个象限内y随x的增大而减小;②k<0时,函数图象在第二,四象限.在每个象限内y随x的增大而增大.
13.【答案】12
【解析】解:根据两个转盘的形状,画树状图如下:
共有6种等可能的结果,其中转到红色和蓝色的结果有3种,
∴配得紫色的概率为36=12.
故答案为:12.
画树状图得出所有等可能的结果数和配得紫色的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
14.【答案】32π
【解析】解:作AD⊥BC于点D,作BE⊥AC于点E,AD和BE交于点O,如图所示,
∵AB=6,△ABC是等边三角形,
∴BD=3,∠OBD=30°,
∵∠ADB=90°,
∴OB=2OD,OB2=OD2+BD2,
∴OD= 3,
∴圆中的黑色部分的面积是:12π×( 3)2=32π,
故答案为:32π.
根据题意和图形,可知圆中的黑色部分的面积是圆的面积的一半,然后即可计算出圆中的黑色部分的面积.
本题考查等边三角形的性质、圆的面积、三角形的内切圆与内心,解答本题的关键是明确题意,利用数形结合的思想解答.
15.【答案】1≤d<5
【解析】解:∵∠ACB=90°,AB=6,BC=8,
∴AC= AB2+BC2= 62+82=10,
如图,设C1D与BC交于点F,作点D关于直线BC的对称点D′,连接DD′交BC于G,
∵点D与点D′关于BC对称,
∴DD′⊥BC,DG=D′G,
∵∠CGD=∠ABC=90°,
∴DG//AB,
∴△CDG∽△CAB,
∴DGAB=CDAC,
∵点D为AC的中点,
∴CD=12AC,即CDAC=12,
∴DG6=12,
∴DG=3,
∴DD′=6,
连接C2D′,FD′,则FD′与FD关于直线BC对称,
∵FC1、FC2关于直线BC对称,且点C1,F,D共线,点C2,F,D′共线,且C2D′=C1D=CD=5,点C2在以点D′为圆心,5为半径的BC上运动,
∴当点C2在DD′上时,点D、C2之间的距离最小,最小值为6−5=1,
又∵d<5,
∴d的取值范围为1≤d<5.
故答案为:1≤d<5.
由勾股定理可得AC=10,设C1D与BC交于点F,作点D关于直线BC的对称点D′,连接DD′交BC于G,由DG//AB,点D为AC的中点,可得DD′=6,连接C2D′,FD′,则FD′与FD关于直线BC对称,由对称性可得点C2在以点D′为圆心,5为半径的BC上运动,即可得出答案.
本题考查了折叠的性质、三角形中位线定理、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理、圆外一点到圆上点的距离最值等知识,熟练掌握折叠的性质,证明三角形全等和三角形相似是解题的关键.
16.【答案】解:(1)(π−1)0−2sin60°+ 3−|−3|
=1−2× 32+ 3−3
=1− 3+ 3−3
=−2;
(2)(x2+1x−2)÷x2−1x
=x2+1−2xx⋅x(x+1)(x−1)
=(x−1)2x⋅x(x+1)(x−1)
=x−1x+1.
【解析】(1)先化简各式,然后再进行计算即可解答;
(2)先利用异分母分式加减法法则计算括号里,再算括号外,即可解答.
本题考查了分式的混合运算,实数的运算,零指数幂,特殊角的三角函数值,准确熟练地进行计算是解题的关键.
17.【答案】7 7 7
【解析】解:(1)甲班10名同学进球数从小到大排列为:5、5、5、7、7、7、7、8、9、10,7出现的次数最多,
所以中位数a=7+72=7,众数b=7,
乙班10名同学进球平均数为:110×(5×2+7×5+8×2+9×1)=7(个),
∴c=7,
故答案为:7,7,7;
(2)乙班,理由如下:
乙班选手进球数的方差为:S乙2=110×[(9−7)2+2×(8−7)2+5×(7−7)2+2×(5−7)2]=1.4;
根据题意得:两个班成绩的平均数,中位数,众数相同,但甲班选手进球数的方差大于乙班选手进球数的方差,
∴乙班选手成绩更稳定,
∴应选乙班.
(1)利用加权平均数、中位数和众数的定义直接求出;
(2)根据方差和个人发挥的最好成绩进行选择.
本题考查了平均数,中位数,众数和方差的意义,掌握相关知识是解题的关键.
18.【答案】解:(1)设y与x的函数关系式为y=kx(k≠0),
将(15,4)代入,得15=k4.
∴k=4×15=60,
∴y与x的函数关系式为y=60x(x≥6);
(2)当x=6时y=60x=10,
∴点A的坐标为(6,10);
由A点(6,10)可得OA所在直线表达式为y=106x=53x,
将y=1.5代入y=5x,得53x=1.5,
∴x=0.9,
将y=1.5代入y=60x,得60x=1.5,
∴x=40,
∴40−0.9=39.1(分钟),
超过30分钟,故是有效消毒.
【解析】(1)首先根据题意,药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,将数据代入用待定系数法可得反比例函数的关系式;
(2)线求出A点坐标,再求出线段OA的函数解析式,再把y=1.5分别代入两个解析式求出x计算即可.
本题考查了反比例函数的应用,理解正比例函数和反比例函数的性质,掌握待定系数法求函数解析式是解题关键.
19.【答案】解:(1)如图,过点F作FK⊥AB于点K.
∵AB=24cm,AE=6cm,
∴BE=AB−AE=18cm.
∵EF=BF,
∴KB=12BE=9,
∴csB=BKBF=910=0.90,
∴∠B≈26°.
(2)∵FN=3cm,BF=10cm,
∴CN=17cm,
∴sinC=MNCN=1017≈0.59,
∴∠C≈36°.
如图,连接BD.
∵CD=BC,
∴∠CBD=∠CDB=72°,
∴∠ABD=∠CBD+∠CBA=72°+26°≠90°,
∴点D不在点B的正上方.
【解析】(1)如图,过点F作FK⊥AB于点K,构造直角△BFK.在该直角三角形中,BK=9cm,BF=10cm,所以通过∠B的余弦函数定义求解即可;
(2)只需证得∠ABD≠90°即可.
本题主要考查了解直角三角形的应用,等腰三角形的性质,利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
20.【答案】解:(1)设本次试点投放A型车x辆,B型车y辆,
依题意得:x+y=805x+3y=340,
解得:x=50y=30.
答:本次试点投放A型车50辆,B型车30辆.
(2)设该市民一年内使用m次共享汽车,则选择优惠卡租车所需费用为18m元,选择VIP卡租车所需费用为(1680+12m)元.
当18m<1680+12m时,m<280,
∴该市民一年内用车少于280次时,选择优惠卡方式租车合算;
当18m=1680+12m时,m=280,
∴该市民一年内用车280次时,选择两种租车方式所需费用相同;
当18m>1680+12m时,m>280,
∴该市民一年内用车多于280次时,选择VIP卡方式租车合算.
答:该市民一年内用车少于280次时,选择优惠卡方式租车合算;该市民一年内用车280次时,选择两种租车方式所需费用相同;该市民一年内用车多于280次时,选择VIP卡方式租车合算.
【解析】(1)设本次试点投放A型车x辆,B型车y辆,利用总价=单价×数量,结合投放A,B两种款型的汽车共80辆且总价值为340万元,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设该市民一年内使用m次共享汽车,则选择优惠卡租车所需费用为18m元,选择VIP卡租车所需费用为(1680+12m)元,分18m<1680+12m,18m=1680+12m及18m>1680+12m三种情况,求出m的取值范围或m的值,进而可得出结论.
本题考查了二元一次方程组的应用、一元一次不等式的应用、列代数式以及一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,用含m的代数式表示出选择两种租车方式所需费用.
21.【答案】(1)证明:如图,连接OC,
∵点D是AC的中点,
∴∠AOD=∠COD=12∠AOC,
又∵∠B=12∠AOC,
∴∠B=∠AOD,
∴OD//BC;
(2)解:如图,连接AC,交OD于点E,设⊙O的半径为r,则OD=OC=r,
∵DE=2,
∴OE=r−2,
∵OA=OC,∠AOD=∠COD,
∴OD⊥AC,
∴∠AEO=∠CEO=90°,AE=EC=12AC=12×8=4,
在Rt△CEO中,OC2=CE2+OE2,r2=42+(r−2)2,
解得r=5,
∴⊙O的半径为5.
【解析】(1)连接OC,根据点D是AC的中点及圆周角定理,可以证得∠B=∠AOD,据此即可证得结论;
(2)连接AC,交OD于点E,设⊙O的半径为r,则OD=OC=r,OE=r−2,首先根据等腰三角形的性质可证得∠AEO=∠CEO=90°,AE=EC=4,再利用勾股定理列出方程,通过解方程求得相关线段的长度即可.
本题考查了圆周角定理,平行线的判定定理,等腰三角形的性质,勾股定理,熟练掌握和运用各图形的性质是解决本题的关键.
22.【答案】解:(1)设其解析式为:h=at2+bt+c,
把点(0,2),(0.5,9.5),(1,16)代入得:c=20.25a+0.5b+c=9.5a+b+c=16,
解得a=−2b=16c=2,
故相应的函数解析式为:h=−2t2+16t+2;
(2)∵这种烟花每隔2s发射一发花弹,每一发花弹的飞行路径、爆炸时的高度均相同,小杰发射出的第一发花弹的函数表达式为h=−2(t−4)2+34,
∴第二发花弹的函数表达式为h′=−2(t−6)2+34.
皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,
则令h=h′,得−2(t−4)2+34=−2(t−6)2+34,
解得t=5,此时h=h′=32>30m,
故花弹的爆炸高度符合安全要求.
【解析】(1)相应的函数解析式为:h=−2(t−3)2+19.8;
(2)第二发花弹达到的高度为6.28 m;
(3)花弹的爆炸高度符合安全要求.
本题考查了二次函数的应用,需要先根据表格中数据描点,得出函数图象,再求出其解析式,分析变化趋势,可以代值验算,第三问需要从实际问题分析转变成数学模型,从而得解.
23.【答案】DE=DF
【解析】(1)解:①DE=DF;
∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵点D为BC的中点,
∴DB=DC,
∵DE⊥AB,
∴∠DEB=90°,
∴∠EDB=90°−∠B=30°,
∵∠EDF=120°,
∴∠FDC=180°−∠EDB−∠EDF=30°,
∴∠EDB=∠FDC,
∴△DBE≌△△DCF(ASA),
∴DE=DF;
故答案为:DE=DF;
②DE=DF仍然成立;
将DB绕点D顺时针旋转120°,交于AC于点B′,如图所示:
∵∠BDB′=120°,
∴∠B′DC=180°−120°=60°,
∴∠B=∠B′DC=60°,
∴DB′//AB,
∴∠DB′C=∠BAC=60°,
∴∠B=∠DB′C,
∴△DCB′为等边三角形,
∴DB′=DC=DB,
∵∠BDE+∠EDB′=120°,∠EDB′+∠B′DF=120°,
∴∠BDE=∠B′DF,
∴△DBE≌△DB′F(ASA),
∴DE=DF;
(2)解:①当点E在A,B两点之间时,将DB绕点D顺时针旋转120°,交AC于点B′,如图所示:
设等边三角形的边长为a,
∵AE:BE=3:2,
∴BE=25a,
∵∠BDB′=120°,
∴∠B′DC=180°−120°=60°,
∴∠B=∠B′DC=60°,
∴DB′//AB,
∴∠DB′C=∠BAC=60°,
∴∠B=∠DB′C,
∴△DCB′是等边三角形,
∴DB′=DC=CB′=13a,
∵∠BDE+∠EDB′=120°,∠EDB′+∠B′DF=120°,
∴∠BDE=∠B′DF,
∴△DBE∽△DB′F,
∴B′FBE=DB′DB=12,
∴B′F=12BE=12×25a=15a,
∴CF=B′C−B′F=13a−15a=215a,
∴AF=a−CF=215a=1315a,
∴CFAF=215a1315a=213;
②当点E在B点下方时,将DB绕D点顺时针旋转120°,交于AC于点B′,如图所示:
设等边三角形的边长为a,
∵AE:BE=3:2,
∴BE=2a,
∵∠BDB′=120°,
∴∠B′DC=180°−120°=60°,
∴∠ABC=∠B′DC=60°,
∴DB′//AB,
∴∠DB′C=∠BAC=60°,
∴∠ABC=∠DB′C=60°,
∴△DCB′是等边三角形,
∴180°−∠ABC=180°−∠DB′C,
即∠DBE=∠DB′F,
∴DB′=DC=CB′=13a,
∵∠BDE+∠EDB′=120°,∠EDB′+∠B′DF=120°,
∴∠BDE=∠B′DF,
∴△DBE∽△DB′F,
∴B′FBE=DB′DB=12,
∴B′F=12BE=12×2a=a,
∴CF=B′C+B′F=13a+a=43a,
∴AF=CF−a=43a−a=13a,
∴CFAF=43a13a=4;
综上所述,CFAF的值为213或4.
(1)①根据ASA证明△DBE和△DCF全等,进而利用全等三角形的性质解答即可;
②将DB绕点D顺时针旋转120°,交于AC于点B′,则证明△DBE和△DB′F全等,进而利用全等三角形的性质解答即可;
(2)分①当点E在A,B两点之间时,②当点E在B点下方时,两种情况,利用相似三角形的判定和性质解答即可.
此题考查几何变换的综合题,关键是根据等边三角形的性质、全等三角形的判定和性质以及相似三角形的判定和性质解答.
班级
平均数
中位数
众数
甲
7
b
c
乙
a
7
7
飞行时间t/s
0
0.5
1
4.5
…
飞行高度h/m
2
9.5
16
33.5
…
第I卷(选择题)
一、选择题(本大题共10小题,共30.0分。在每小题列出的选项中,选出符合题目的一项)
1. 下列各数中,最小的有理数是( )
A. −2023B. 0C. 12023D. −2022
2. 如图所示的几何体的主视图是( )
A.
B.
C.
D.
3. 已知显微镜下肆虐横行的被人们称为“大毒王”的新冠病毒变异毒株奥密克戎直径约为0.0000001米,该长度用科学记数法表示为( )
A. 10×106米B. 10−6米C. 10−7米D. 0.1×10−6米
4. 如图,直线AB,CD相交于点O,EO⊥AB,垂直为点O,∠BOD=50°,则∠COE=( )
A. 30°B. 50°C. 120°D. 140°
5. 下列运算正确的是( )
A. a2+a2=2a4B. 3a2−2a3=6a6
C. (−2ab3)2=4a2b6D. a6÷a2=a3
6. 不等式组3x<2x+12x+5≥−1的解集在数轴上表示正确的是( )
A. B.
C. D.
7. 如图①所示,平整的地面上有一个不规则图案(图中阴影部分),小明想了解该图案的面积是多少,他采取了以下办法:用一个面积为20cm2的长方形,将不规则图案围起来,然后在适当位置随机地朝长方形区域扔小球,并记录小球落在不规则图案上的次数(球扔在界线上或长方形区域外不计试验结果),他将若干次有效试验的结果绘制成了②所示的折线统计图,由此他估计不规则图案的面积大约为( )
A. 6cm2B. 7cm2C. 8 cm2D. 9cm2
8. 已知a,b,c为常数,点P(a,c)在第四象限,则关于x的一元二次方程ax2+bx+c=0的根的情况为( )
A. 有两个相等的实数根B. 有两个不相等的实数根
C. 没有实数根D. 无法判定
9. A、B两地相距80km,甲、乙两人沿同一条路从A地到B地.l1,l2分别表示甲、乙两人离开A地的距离s(km)与时间t(h)之间的关系.对于以下说法:①乙车出发1.5小时后甲才出发;②两人相遇时,他们离开A地20km;③甲的速度是40km/h,乙的速度是403km/h;④当乙车出发2小时时,两车相距13km.其中正确的结论是( )
A. ①③B. ①④C. ②③D. ②④
10. 在平面直角坐标系中,菱形OABC的位置如图所示,其中点B的坐标为(1,1),第1次将菱形OABC绕着点O逆时针旋转90°,同时扩大为原来的2倍得到菱形OA1B1C1(即OB1=2OB),第2次将菱形OA1B1C1绕着点O逆时针再旋转90°,同时扩大为原来的2倍得到菱形OA2B2C2(即OB2=2OB1),第3次将菱形OA2B2C2绕着点O逆时针再旋转90°,同时扩大为原来的2倍得到菱形OA3B3C3(即OB3=2OB2)…,依次类推,则点B2023的坐标为( )
A. (22023,−22023)B. (−22023,−22023)C. (−22023,22023)D. (22023,22023)
第II卷(非选择题)
二、填空题(本大题共5小题,共15.0分)
11. 若代数式1x−1有意义,则实数x的取值范围是 .
12. 写出一个函数,当x>0时,y随x的增大而减小,这个函数的解析式可以是 .
13. 用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是______.(红色和蓝色配成紫色)
14. 如图,等边△ABC内切圆的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称.若等边△ABC的边长为6,则圆中的黑色部分的面积是 .
15. 如图,直角三角形纸片ABC中,∠ABC=90°,AB=6,BC=8.点D为AC的中点,点E为BC一动点(不与端点重合),且CE<4,沿直线DE折叠该纸片,点C的对应点为C1,再沿直线BC折叠该纸片,点C的对应点为C2,设点C2,D之间的距离为d,则d的取值范围为______ .
三、解答题(本大题共8小题,共75.0分。解答应写出文字说明,证明过程或演算步骤)
16. (本小题10.0分)
(1)计算:(π−1)0−2sin60°+ 3−|−3|;
(2)化简:(x2+1x−2)÷x2−1x.
17. (本小题9.0分)
甲、乙两班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,根据两个班选手的进球数,制作了如下统计图及数据分析表.
(1)写出表格中a,b,c的值:a= ______ ,b= ______ ,c= ______ ;
(2)如果要从这两个班中选出一个班参加学校的投篮比赛,你认为应该选择哪个班比较合适?为什么?
18. (本小题9.0分)
西安市某校为进一步预防“新型冠状病毒”,对全校所有的教室都进行了“熏药法消毒”处理,已知该药物在燃烧释放过程中,教室内空气中每立方米的含药量y(mg)与燃烧时间x(min)之间的函数关系如图所示,其中当x<6时,y是x的正比例函数,当x≥6时,y是x的反比例函数,根据图象提供的信息,解答下列问题:
(1)求当x≥6时,y与x的函数关系式;
(2)药物燃烧释放过程中,若空气中每立方米的含药量不小于1.5mg的时间超过30分钟,即为有效消毒,请问本题中的消毒是否为有效消毒?
19. (本小题9.0分)
图1是电脑及电脑支架实物图,图2是其示意图,DG是电脑屏幕,托杠AB=BC=CD=24cm,支杠MN=EF=10cm,B,M,F为固定点,BF=10cm,支杠MN,EF可分别绕着点M,F旋转,点E,N分别在AB,BC上滑动.当电脑及电脑支架按如图所示的方式放置时,AE=6cm.
(1)求∠B的度数.
(2)当FN=3cm,MN⊥CD时,试通过计算说明点D是否位于点B的正上方.(参考数据:sin36°≈0.59,cs26°≈0.90,sin18°≈0.31)
20. (本小题9.0分)
近两年,共享经济快速崛起,共享汽车、共享单车、共享雨伞、共享KTV、共享充电宝等等.现南宁市计划在城区再投放一批“共享新能源汽车”,这批汽车分为A,B两种不同款型,其中A型车单价5万元,B型车单价3万元.
(1)今年年初,“共享新能源汽车”再投放在城区正式启动,投放A,B两种款型的汽车共80辆,总价值340万元.试问本次试点投放的A型车与B型车各多少辆?
(2)为鼓励市民绿色出行,特推出以下优惠活动:
①优惠卡:保证金2500元(还车可退回),每小时内(含1小时)18元;
②VIP卡:会员费1680元(不退还),每小时内(含1小时)12元.
若市民出行每次用车均不超过1小时,如何选择才能使一年内租用共享汽车最合算.
21. (本小题9.0分)
如图,四边形ABCD内接于⊙O,AB是直径,点D是AC的中点.
(1)求证:OD//BC;
(2)连接AC交OD于点E,若AC=8,DE=2,求⊙O的半径.
22. (本小题10.0分)
燃放烟花是一种常见的喜庆活动.如图,小杰燃放一种手持烟花,这种烟花每隔2s发射一枚花弹,每枚花弹的飞行路径视为同一条抛物线,飞行相同时间后发生爆炸,小杰发射出的第一枚花弹的飞行高度h(单位:m)随飞行时间(单位:s)变化的规律如表:
(1)求第一枚花弹的飞行高度h与飞行时间t的函数解析式;(不要求写出自变量的取值范围)
(2)为了安全,要求花弹爆炸时的高度不低于30m.小杰发现在第一枚花弹爆炸的同时,第二枚花弹与它处于同一高度,请分析花弹的爆炸高度是否符合安全要求.
23. (本小题10.0分)
在等边三角形ABC中,点D是线段BC上一点,点E是直线AB上一动点,连接DE,把射线DE绕点D顺时针旋转120°,与直线AC相交于点F.
(1)若点D为线段BC中点.
①如图1,当点E在线段AB上,且DE⊥AB时,请直接写出线段DE与DF的数量关系:______ ;
②如图2,当点E落在线段AB上,点F落在射线AC上时,①中的结论是否仍然成立?请结合图2说明理由;
(2)如图3,若点D为边BC上靠近点G的三等分点.当AE:BE=3:2时,直接写出CFAF的值.
答案和解析
1.【答案】A
【解析】解:∵−2023<−2022<0<12023,
∴最小的有理数是−2023,
故选:A.
根据正数都大于0,负数都小于0,正数大于负数,两个负数,绝对值大的反而小;进行比较,即可求解.
本题考查了有理数的大小比较,熟练掌握有理数大小比较的方法是解答本题的关键.
2.【答案】D
【解析】解:从正面看,是一个等腰三角形.
故选:D.
根据从正面看得到的图形是主视图,可得答案.
本题考查了简单组合体的三视图,从正面看得到的图形是主视图.
3.【答案】C
【解析】解:0.0000001米=10−7米.
故选:C.
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
本题考查了科学记数法表示绝对值较大的数的方法,掌握科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数是关键.
4.【答案】D
【解析】解:∵∠BOD=50°,
∴∠AOC=50°,
∵EO⊥AB,
∴∠COE=90°+50°=140°.
故选:D.
利用对顶角的定义结合垂线的定义得出∠COE=90°+50°求出即可.
此题主要考查了对顶角以及垂线的定义,得出∠AOC度数是解题关键.
5.【答案】C
【解析】解:A、∵a2+a2=2a2,∴本选项错误.
B、∵3a2和2a3不是同类项,∴本选项错误.
C、∵(−2ab3)2=4a2b6,∴本选项正确.
D、∵a6÷a2=a4,∴本选项错误.
故选:C.
利用合并同类项法则,单项式乘单项式,积的乘方性质同底数幂乘除法判断即可.
本题主要考查合并同类项,单项式乘单项式,积的乘方运算与幂的乘方运算,同底数幂的运算,掌握运算法则是解决此题的关键.
6.【答案】C
【解析】解:3x<2x+1①2x+5≥−1②,
解不等式①得:x<1,
解不等式②得:x≥−3,
∴原不等式组的解集为:−3≤x<1,
∴该不等式组的解集在数轴上表示如图所示:
故选:C.
按照解一元一次不等式组的步骤,进行计算即可解答.
本题考查了解一元一次不等式组,在数轴上表示不等式的解集,熟练掌握解一元一次不等式组是解题的关键.
7.【答案】B
【解析】
【分析】
本题分两部分求解,首先设不规则图案的面积为xcm2,根据几何概率知识求解不规则图案占长方形的面积大小,继而根据折线图用频率估算概率,综合以上列方程求解即可.
本题考查几何概率以及用频率估计概率,并在此基础上进行题目创新,解题的关键在于理解题意,能从复杂的题目背景中找到考点化繁为简.
【解答】解:假设不规则图案的面积为xcm2,
由已知得:长方形面积为20cm2,
根据几何概率公式小球落在不规则图案的概率为:x20,
当事件A试验次数足够多,即样本足够大时,其频率可作为事件A发生的概率估计值,故由折线图可知,小球落在不规则图案的概率大约为0.35,
综上:x20=0.35,
解得:x=7,
∴不规则图案的面积大约为7cm2,
故选:B.
8.【答案】B
【解析】解:∵点P(a,c)在第四象限,
∴a>0,c<0,
∴ac<0,
∴方程ax2+bx+c=0的判别式Δ=b2−4ac>0,
∴方程ax2+bx+c=0有两个不相等的实数根.
故选:B.
先利用第二象限点的坐标特征得到ac<0,则判断Δ>0,然后根据判别式的意义判断方程根的情况.
本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与Δ=b2−4ac有如下关系:当Δ>0时,方程有两个不相等的实数根;当Δ=0时,方程有两个相等的实数根;当Δ<0时,方程无实数根.
9.【答案】C
【解析】解:由图可得,
乙车出发1.5小时后甲已经出发一段时间,故①错误;
两人相遇时,他们离开A地20km,故②正确;
甲的速度是(80−20)÷(3−1.5)=40(km/h),乙的速度是40÷3=403(km/h),故③正确;
当乙车出发2小时时,两车相距:[20+40×(2−1.5)]−403×2=403(km),故④错误;
故选:C.
根据题意和函数图象中的数据,可以判断各个小题中的结论是否正确,从而可以解答本题.
本题考查一次函数的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
10.【答案】A
【解析】解:∵点B的坐标为(1,1),第1次将菱形OABC绕着点O逆时针旋转90°,同时扩大为原来的2倍得到菱形OA1B1C1(即OB1=2OB),
∴B1的坐标为(−2,2),
同理:B2的坐标为(−4,−4),即(−22,−22),
B3的坐标为(8,−8),即(23,−23),
B4的坐标为(16,16),即(24,24),
……,
∵2023÷4=505……3,
∴点B2023的坐标为(22023,−22023),
故选:A.
由题意得B1的坐标为(−2,2),同理B2的坐标为(−4,−4),即(−22,−22),B3的坐标为(8,−8),即(23,−23),B4的坐标为(16,16),即(24,24),……,
再由2023÷4=505……3,即可得出结论.
本题考查了菱形的性质、坐标与图形性质以及规律型等知识,找出点Bn的坐标规律是解题的关键.
11.【答案】x≠1
【解析】
【分析】
本题考查了分式有意义的条件,分式有意义的条件是分母不等于零.
分式有意义时,分母x−1≠0,据此求得x的取值范围即可.
【解答】
解:依题意得:x−1≠0,
解得x≠1,
故答案为:x≠1.
12.【答案】y=−2x(x>0),答案不唯一
【解析】解:只要使反比例系数大于0即可.如y=−2x(x>0),答案不唯一.
故答案为:y=−2x(x>0),答案不唯一.
反比例函数的图象在每个象限内,函数值y随自变量x的增大而减小,则反比例函数的反比例系数k<0.
本题主要考查了反比例函数y=kx(k≠0)的性质:①k>0时,函数图象在第一,三象限.在每个象限内y随x的增大而减小;②k<0时,函数图象在第二,四象限.在每个象限内y随x的增大而增大.
13.【答案】12
【解析】解:根据两个转盘的形状,画树状图如下:
共有6种等可能的结果,其中转到红色和蓝色的结果有3种,
∴配得紫色的概率为36=12.
故答案为:12.
画树状图得出所有等可能的结果数和配得紫色的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
14.【答案】32π
【解析】解:作AD⊥BC于点D,作BE⊥AC于点E,AD和BE交于点O,如图所示,
∵AB=6,△ABC是等边三角形,
∴BD=3,∠OBD=30°,
∵∠ADB=90°,
∴OB=2OD,OB2=OD2+BD2,
∴OD= 3,
∴圆中的黑色部分的面积是:12π×( 3)2=32π,
故答案为:32π.
根据题意和图形,可知圆中的黑色部分的面积是圆的面积的一半,然后即可计算出圆中的黑色部分的面积.
本题考查等边三角形的性质、圆的面积、三角形的内切圆与内心,解答本题的关键是明确题意,利用数形结合的思想解答.
15.【答案】1≤d<5
【解析】解:∵∠ACB=90°,AB=6,BC=8,
∴AC= AB2+BC2= 62+82=10,
如图,设C1D与BC交于点F,作点D关于直线BC的对称点D′,连接DD′交BC于G,
∵点D与点D′关于BC对称,
∴DD′⊥BC,DG=D′G,
∵∠CGD=∠ABC=90°,
∴DG//AB,
∴△CDG∽△CAB,
∴DGAB=CDAC,
∵点D为AC的中点,
∴CD=12AC,即CDAC=12,
∴DG6=12,
∴DG=3,
∴DD′=6,
连接C2D′,FD′,则FD′与FD关于直线BC对称,
∵FC1、FC2关于直线BC对称,且点C1,F,D共线,点C2,F,D′共线,且C2D′=C1D=CD=5,点C2在以点D′为圆心,5为半径的BC上运动,
∴当点C2在DD′上时,点D、C2之间的距离最小,最小值为6−5=1,
又∵d<5,
∴d的取值范围为1≤d<5.
故答案为:1≤d<5.
由勾股定理可得AC=10,设C1D与BC交于点F,作点D关于直线BC的对称点D′,连接DD′交BC于G,由DG//AB,点D为AC的中点,可得DD′=6,连接C2D′,FD′,则FD′与FD关于直线BC对称,由对称性可得点C2在以点D′为圆心,5为半径的BC上运动,即可得出答案.
本题考查了折叠的性质、三角形中位线定理、全等三角形的判定与性质、相似三角形的判定与性质、勾股定理、圆外一点到圆上点的距离最值等知识,熟练掌握折叠的性质,证明三角形全等和三角形相似是解题的关键.
16.【答案】解:(1)(π−1)0−2sin60°+ 3−|−3|
=1−2× 32+ 3−3
=1− 3+ 3−3
=−2;
(2)(x2+1x−2)÷x2−1x
=x2+1−2xx⋅x(x+1)(x−1)
=(x−1)2x⋅x(x+1)(x−1)
=x−1x+1.
【解析】(1)先化简各式,然后再进行计算即可解答;
(2)先利用异分母分式加减法法则计算括号里,再算括号外,即可解答.
本题考查了分式的混合运算,实数的运算,零指数幂,特殊角的三角函数值,准确熟练地进行计算是解题的关键.
17.【答案】7 7 7
【解析】解:(1)甲班10名同学进球数从小到大排列为:5、5、5、7、7、7、7、8、9、10,7出现的次数最多,
所以中位数a=7+72=7,众数b=7,
乙班10名同学进球平均数为:110×(5×2+7×5+8×2+9×1)=7(个),
∴c=7,
故答案为:7,7,7;
(2)乙班,理由如下:
乙班选手进球数的方差为:S乙2=110×[(9−7)2+2×(8−7)2+5×(7−7)2+2×(5−7)2]=1.4;
根据题意得:两个班成绩的平均数,中位数,众数相同,但甲班选手进球数的方差大于乙班选手进球数的方差,
∴乙班选手成绩更稳定,
∴应选乙班.
(1)利用加权平均数、中位数和众数的定义直接求出;
(2)根据方差和个人发挥的最好成绩进行选择.
本题考查了平均数,中位数,众数和方差的意义,掌握相关知识是解题的关键.
18.【答案】解:(1)设y与x的函数关系式为y=kx(k≠0),
将(15,4)代入,得15=k4.
∴k=4×15=60,
∴y与x的函数关系式为y=60x(x≥6);
(2)当x=6时y=60x=10,
∴点A的坐标为(6,10);
由A点(6,10)可得OA所在直线表达式为y=106x=53x,
将y=1.5代入y=5x,得53x=1.5,
∴x=0.9,
将y=1.5代入y=60x,得60x=1.5,
∴x=40,
∴40−0.9=39.1(分钟),
超过30分钟,故是有效消毒.
【解析】(1)首先根据题意,药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,将数据代入用待定系数法可得反比例函数的关系式;
(2)线求出A点坐标,再求出线段OA的函数解析式,再把y=1.5分别代入两个解析式求出x计算即可.
本题考查了反比例函数的应用,理解正比例函数和反比例函数的性质,掌握待定系数法求函数解析式是解题关键.
19.【答案】解:(1)如图,过点F作FK⊥AB于点K.
∵AB=24cm,AE=6cm,
∴BE=AB−AE=18cm.
∵EF=BF,
∴KB=12BE=9,
∴csB=BKBF=910=0.90,
∴∠B≈26°.
(2)∵FN=3cm,BF=10cm,
∴CN=17cm,
∴sinC=MNCN=1017≈0.59,
∴∠C≈36°.
如图,连接BD.
∵CD=BC,
∴∠CBD=∠CDB=72°,
∴∠ABD=∠CBD+∠CBA=72°+26°≠90°,
∴点D不在点B的正上方.
【解析】(1)如图,过点F作FK⊥AB于点K,构造直角△BFK.在该直角三角形中,BK=9cm,BF=10cm,所以通过∠B的余弦函数定义求解即可;
(2)只需证得∠ABD≠90°即可.
本题主要考查了解直角三角形的应用,等腰三角形的性质,利用数学知识解决实际问题是中学数学的重要内容.解决此问题的关键在于正确理解题意的基础上建立数学模型,把实际问题转化为数学问题.
20.【答案】解:(1)设本次试点投放A型车x辆,B型车y辆,
依题意得:x+y=805x+3y=340,
解得:x=50y=30.
答:本次试点投放A型车50辆,B型车30辆.
(2)设该市民一年内使用m次共享汽车,则选择优惠卡租车所需费用为18m元,选择VIP卡租车所需费用为(1680+12m)元.
当18m<1680+12m时,m<280,
∴该市民一年内用车少于280次时,选择优惠卡方式租车合算;
当18m=1680+12m时,m=280,
∴该市民一年内用车280次时,选择两种租车方式所需费用相同;
当18m>1680+12m时,m>280,
∴该市民一年内用车多于280次时,选择VIP卡方式租车合算.
答:该市民一年内用车少于280次时,选择优惠卡方式租车合算;该市民一年内用车280次时,选择两种租车方式所需费用相同;该市民一年内用车多于280次时,选择VIP卡方式租车合算.
【解析】(1)设本次试点投放A型车x辆,B型车y辆,利用总价=单价×数量,结合投放A,B两种款型的汽车共80辆且总价值为340万元,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设该市民一年内使用m次共享汽车,则选择优惠卡租车所需费用为18m元,选择VIP卡租车所需费用为(1680+12m)元,分18m<1680+12m,18m=1680+12m及18m>1680+12m三种情况,求出m的取值范围或m的值,进而可得出结论.
本题考查了二元一次方程组的应用、一元一次不等式的应用、列代数式以及一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,用含m的代数式表示出选择两种租车方式所需费用.
21.【答案】(1)证明:如图,连接OC,
∵点D是AC的中点,
∴∠AOD=∠COD=12∠AOC,
又∵∠B=12∠AOC,
∴∠B=∠AOD,
∴OD//BC;
(2)解:如图,连接AC,交OD于点E,设⊙O的半径为r,则OD=OC=r,
∵DE=2,
∴OE=r−2,
∵OA=OC,∠AOD=∠COD,
∴OD⊥AC,
∴∠AEO=∠CEO=90°,AE=EC=12AC=12×8=4,
在Rt△CEO中,OC2=CE2+OE2,r2=42+(r−2)2,
解得r=5,
∴⊙O的半径为5.
【解析】(1)连接OC,根据点D是AC的中点及圆周角定理,可以证得∠B=∠AOD,据此即可证得结论;
(2)连接AC,交OD于点E,设⊙O的半径为r,则OD=OC=r,OE=r−2,首先根据等腰三角形的性质可证得∠AEO=∠CEO=90°,AE=EC=4,再利用勾股定理列出方程,通过解方程求得相关线段的长度即可.
本题考查了圆周角定理,平行线的判定定理,等腰三角形的性质,勾股定理,熟练掌握和运用各图形的性质是解决本题的关键.
22.【答案】解:(1)设其解析式为:h=at2+bt+c,
把点(0,2),(0.5,9.5),(1,16)代入得:c=20.25a+0.5b+c=9.5a+b+c=16,
解得a=−2b=16c=2,
故相应的函数解析式为:h=−2t2+16t+2;
(2)∵这种烟花每隔2s发射一发花弹,每一发花弹的飞行路径、爆炸时的高度均相同,小杰发射出的第一发花弹的函数表达式为h=−2(t−4)2+34,
∴第二发花弹的函数表达式为h′=−2(t−6)2+34.
皮皮发现在第一发花弹爆炸的同时,第二发花弹与它处于同一高度,
则令h=h′,得−2(t−4)2+34=−2(t−6)2+34,
解得t=5,此时h=h′=32>30m,
故花弹的爆炸高度符合安全要求.
【解析】(1)相应的函数解析式为:h=−2(t−3)2+19.8;
(2)第二发花弹达到的高度为6.28 m;
(3)花弹的爆炸高度符合安全要求.
本题考查了二次函数的应用,需要先根据表格中数据描点,得出函数图象,再求出其解析式,分析变化趋势,可以代值验算,第三问需要从实际问题分析转变成数学模型,从而得解.
23.【答案】DE=DF
【解析】(1)解:①DE=DF;
∵△ABC为等边三角形,
∴∠B=∠C=60°,
∵点D为BC的中点,
∴DB=DC,
∵DE⊥AB,
∴∠DEB=90°,
∴∠EDB=90°−∠B=30°,
∵∠EDF=120°,
∴∠FDC=180°−∠EDB−∠EDF=30°,
∴∠EDB=∠FDC,
∴△DBE≌△△DCF(ASA),
∴DE=DF;
故答案为:DE=DF;
②DE=DF仍然成立;
将DB绕点D顺时针旋转120°,交于AC于点B′,如图所示:
∵∠BDB′=120°,
∴∠B′DC=180°−120°=60°,
∴∠B=∠B′DC=60°,
∴DB′//AB,
∴∠DB′C=∠BAC=60°,
∴∠B=∠DB′C,
∴△DCB′为等边三角形,
∴DB′=DC=DB,
∵∠BDE+∠EDB′=120°,∠EDB′+∠B′DF=120°,
∴∠BDE=∠B′DF,
∴△DBE≌△DB′F(ASA),
∴DE=DF;
(2)解:①当点E在A,B两点之间时,将DB绕点D顺时针旋转120°,交AC于点B′,如图所示:
设等边三角形的边长为a,
∵AE:BE=3:2,
∴BE=25a,
∵∠BDB′=120°,
∴∠B′DC=180°−120°=60°,
∴∠B=∠B′DC=60°,
∴DB′//AB,
∴∠DB′C=∠BAC=60°,
∴∠B=∠DB′C,
∴△DCB′是等边三角形,
∴DB′=DC=CB′=13a,
∵∠BDE+∠EDB′=120°,∠EDB′+∠B′DF=120°,
∴∠BDE=∠B′DF,
∴△DBE∽△DB′F,
∴B′FBE=DB′DB=12,
∴B′F=12BE=12×25a=15a,
∴CF=B′C−B′F=13a−15a=215a,
∴AF=a−CF=215a=1315a,
∴CFAF=215a1315a=213;
②当点E在B点下方时,将DB绕D点顺时针旋转120°,交于AC于点B′,如图所示:
设等边三角形的边长为a,
∵AE:BE=3:2,
∴BE=2a,
∵∠BDB′=120°,
∴∠B′DC=180°−120°=60°,
∴∠ABC=∠B′DC=60°,
∴DB′//AB,
∴∠DB′C=∠BAC=60°,
∴∠ABC=∠DB′C=60°,
∴△DCB′是等边三角形,
∴180°−∠ABC=180°−∠DB′C,
即∠DBE=∠DB′F,
∴DB′=DC=CB′=13a,
∵∠BDE+∠EDB′=120°,∠EDB′+∠B′DF=120°,
∴∠BDE=∠B′DF,
∴△DBE∽△DB′F,
∴B′FBE=DB′DB=12,
∴B′F=12BE=12×2a=a,
∴CF=B′C+B′F=13a+a=43a,
∴AF=CF−a=43a−a=13a,
∴CFAF=43a13a=4;
综上所述,CFAF的值为213或4.
(1)①根据ASA证明△DBE和△DCF全等,进而利用全等三角形的性质解答即可;
②将DB绕点D顺时针旋转120°,交于AC于点B′,则证明△DBE和△DB′F全等,进而利用全等三角形的性质解答即可;
(2)分①当点E在A,B两点之间时,②当点E在B点下方时,两种情况,利用相似三角形的判定和性质解答即可.
此题考查几何变换的综合题,关键是根据等边三角形的性质、全等三角形的判定和性质以及相似三角形的判定和性质解答.
班级
平均数
中位数
众数
甲
7
b
c
乙
a
7
7
飞行时间t/s
0
0.5
1
4.5
…
飞行高度h/m
2
9.5
16
33.5
…












