2020北京四中初一（上）期中数学（教师版）

这是一份2020北京四中初一（上）期中数学（教师版），共23页。试卷主要包含了其中正确的所有结论是等内容，欢迎下载使用。

2020北京四中初一（上）期中
数 学
考生须知
1．本试卷共8页，A卷26道题，B卷4道题，共30道题．考试时间100分钟．
2．在试卷和答题卡上准确填写班级、姓名和学号．
3．答案一律填写在答题纸上，在试卷上作答无效．
4．考试结束后，将试卷和答题纸一并交回．
A卷
一、选择题
1. 2020年北京故宫迎来了600岁生日，系列展览与活动让故宫充分展示其深沉魅力．据不完全统计，今年“十一”双节期间故宫累计接待观众约240000人次．将240000用科学记数法可表示为（ ）
A. B. C. D.
2. 的倒数是（　　）
A. 5 B. C. D.
3. 下列各式结果为负数的是（　　）
A ﹣（﹣1） B. （﹣1）4 C. ﹣|﹣1| D. |1﹣2|
4. 下面合并同类项正确的是（ ）
A. B.
C. D.
5. 下列各式去括号正确的是（ ）
A. B.
C. D.
6. 有理数、、在数轴上的对应点的位置如图所示，若与互为相反数，则、、三个数中绝对值最大的数是（ ）

A. B. C. D. 无法确定
7. 下列对使用四舍五入法得到的近似数描述正确的是（ ）
A. 近似数5.1万精确到十分位
B. 2.709的近似数是3
C. 0.154精确到十分位为0.1
D. 近似数精确到千位
8. 若|a|=8，|b|=5，且a+b>0，那么a-b的值是（ ）
A. 3或13 B. 13或-13 C. 3或-3 D. -3或-13
9. 关于的方程是—元—次方程，则的值是（ ）
A. －1 B. 1 C. 1或－1 D. 2
10. 规定：，．例如，．下列结论中：①若，则；②若，则；③能使成立的的值不存在；④式子的最小值是7．其中正确的所有结论是（ ）
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
二、填空题
11. 如果水位升高3m时，水位变化记作，那么水位下降3m时，水位变化记作______
12. 比较大小：________（填“ > ”“ < ” = “）
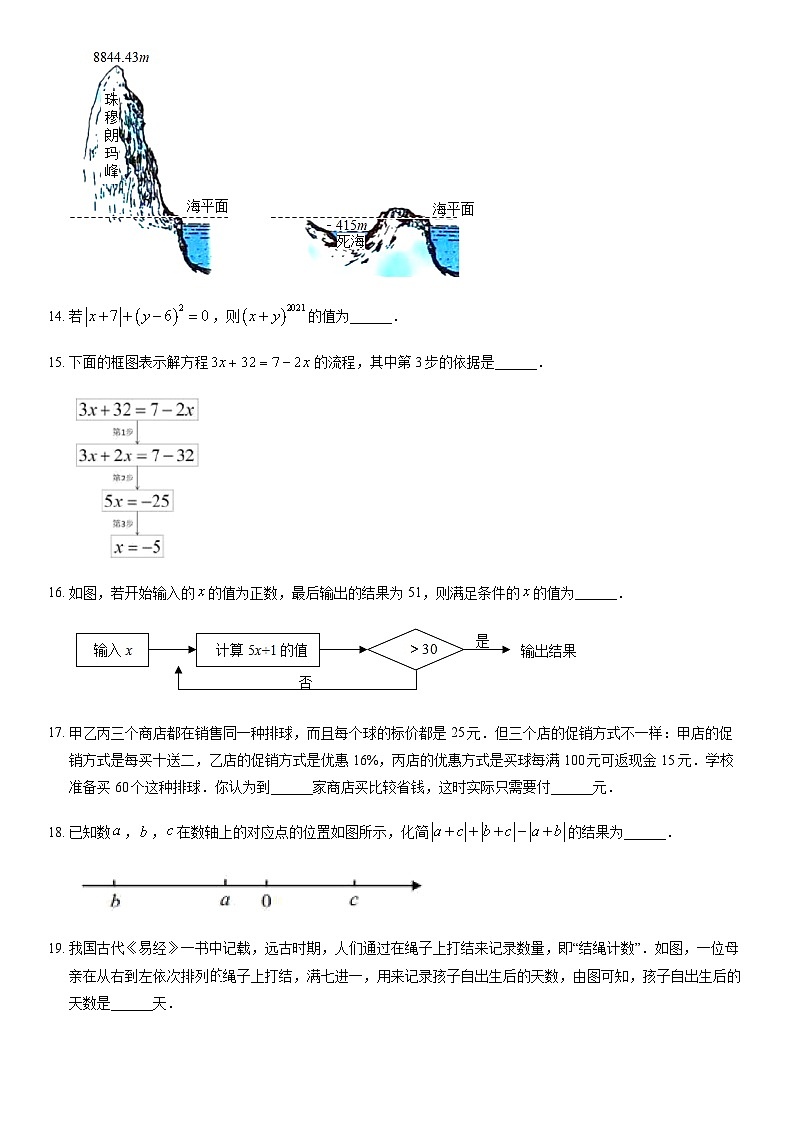
13. 如图所示，大陆上最高处是珠穆朗玛峰的峰顶，最低处位于亚洲西部名为死海的湖，两处高度相差是______米．

14. 若，则的值为______．
15. 下面的框图表示解方程的流程，其中第3步的依据是______．

16. 如图，若开始输入的的值为正数，最后输出的结果为51，则满足条件的的值为______．

17. 甲乙丙三个商店都在销售同一种排球，而且每个球的标价都是25元．但三个店的促销方式不一样：甲店的促销方式是每买十送二，乙店的促销方式是优惠16%，丙店的优惠方式是买球每满100元可返现金15元．学校准备买60个这种排球．你认为到______家商店买比较省钱，这时实际只需要付______元．
18. 已知数，，在数轴上的对应点的位置如图所示，化简的结果为______．

19. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”．如图，一位母亲在从右到左依次排列绳子上打结，满七进一，用来记录孩子自出生后的天数，由图可知，孩子自出生后的天数是______天．

20. 如下数表是由从1开始连续自然数组成，观察规律并完成各题的解答．
1
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
17 18 19 20 21 22 23 24 25
26 27 28 29 30 31 32 33 34 35 36
……………………………………
（1）表中第9行第7个数是______；
（2）2020表中第______行第______个数．
三、解答题
21. 计算
（1）

（2）

（3）

（4）
22. 化简
（1） （2）

23. 解方程
（1） （2）

24. 先化简，再求值：求代数式的值，其中，．

25. 对于任意四个有理数，，，，可以组成两个有理数对与．我们规定：．例如：．根据上述规定解决下列问题：
（1）有理数对______；
（2）若有理数对，则______
（3）当满足等式的是整数时，求整数的值．
26. 在数轴上，表示数的点到原点的距离．如果数轴上两个点、分别对应数、，那么、两点间的距离为：，这是绝对值的几何意义．已知如图，点在数轴上对应的数为－3，点对应的数为2．
（1）求线段的长．
（2）若点在数轴上对应的数为，且是方程的解，在数轴上是否存在点，使？若存在，求出点对应的数；若不存在说明理由．
（3）若点是数轴上在点左侧的一点，线段的中点为点，点为线段的三等分点且靠近于点，当点在点左侧的数轴上运动时，请直接判断的值是否变化，如果不变请直接写出其值，如果变化请说明理由．

B卷
27. （1）桌子上有5只杯口朝上的茶杯，每次翻转3只，经过次翻转可使这5只杯子的杯口全部朝下，则的最小值为______．
（2）桌子上有11只杯口朝上的茶杯，每次翻转3只，经过次翻转可使这11只杯子的杯口全部朝下，则的最小值为______．
28. 如下表，从左向右依次在每个小格子中都填入一个有理数，使得其中任意四个相邻小格子中所填数之和都等于15．已知第3个数为7，第5个数为，第16个数为2，第78个数为，则的值为______，第2021个数为______．


7










29. 天坛中的数学一瞥：天坛始建于明朝永乐十八年（1420年），明、清两代是帝王祭祀皇天、祈五谷丰登之场所．中和韶乐在中国古代的发生、发展、沉寂、经历了历代传承．随着对中国传统文化重新认识，中和韶乐逐渐复苏．自从2004年9月天坛神乐署修复完成，中和韶乐又一次展现在世人面前．中和韶乐主要是宫、商、角、徴、羽五声音阶的运用，在确定这五音的时候，中国古代最初由三分损益计算而来，从最初的一个音三分损一而得到第二个音，由第二个音三分益一得到第三个音，如此计算，得到宫商角徴羽五声音阶．例如：假设能发出第一个基准音的乐器的长度为81，那么能发出第二个基准音的乐器的长度为，能发出第三个基准音的乐器的长度为，（也就是依次先减少三分之一，后增加三分之一）．那么第五个基准音的乐器的长度为______．假设能发出第一个基准音的乐器的长度为，那么能发出第四个基准音的乐器的长度是32，则的值是______．
30. 阅读材料：你知道“二维码”吗？它是一种编码，通过表示1和0的黑白小方块排列成图案传递信息．二维码广泛应用于我们生活，“扫一扫”成为人们的习惯动作．你知道二维码究竟是怎样生成的吗？你想亲自制作一个二维码吗？首先来了解一个定义：“定义符合”表示一种运算叫做“异或”运算，即当时，结果为0；当时，结果为1，下面就让我们试着为“”制作一个二维码吧！
【步骤一】查表可得字母“”的八位二进制编码为01000010，“”为01001000，“”为01010011，“”为01000110．
【步骤二】将每个字母的编码按照一定的顺序排布在方格内，例如字母“”的编码排布如下图第一个表格．然后将编码排布与事先排布好0与1的表格（称为掩模）进行“方格一一对应”的“异或”运算（如下图第三个表格），并将结果中1的位置填涂黑色，0的位置填涂白色（如下图第四个表格）．
解决问题：（1）根据上面的定义将表格补充完整．
（2）仿照上面【步骤二】，完成“”的编码排布、运算及二维码填涂．“”二维码的其余部分已生成，你可以将获得的结果填涂在对于的空白位置．一个完整的二维码就大功告成啦，试着扫一扫它吧！



0
0
0
1
0
1
0
1

1

0



2020北京四中初一（上）期中数学
参考答案
一、选择题
1. 【答案】B
【解析】
【分析】
将240000写成a×10n的形式 （1＜| a |＜10，n为正整数）即可．
【详解】解：240000=．
故答案为B．
【点睛】本题考查了科学记数法，将原数a×10n的形式 （1＜| a |＜10，n为正整数），确定a和n的值是解答本题的关键．
2. 【答案】D
【解析】
【分析】
根据倒数的定义作答．
【详解】-5的倒数是，
故选：D．
【点睛】本题考查了倒数，倒数的定义：若两个数的乘积是1，我们就称这两个数互为倒数．
3. 【答案】C
【解析】
A. -(-1)=1，故A选项不符合题意；B. (-1)4 =1，故B选项不符合题意；C. -|-1|=-1，故C选项符合题意；D. |1-2|=1，故D选项不符合题意，
故选C.
4. 【答案】D
【解析】
试题解析：3x与2x2不是同类项，不能加减，故选项A错误；
2a2b-2a2b-a2b=（2-2-1）a2b=-a2b≠1，-ab-ab=（-1-1）ab=-2ab≠0，故选项B、C均不正确；
-xy2+xy2=（-1+1）xy2=0，故选项D正确．
故选D．
5. 【答案】C
【解析】
【分析】
根据去括号的法则逐项判断即可求解．
【详解】解：A. ，原题计算错误，不合题意；
B. ，原题计算错误，不合题意；
C. ，原题计算正确，符合题意；
D. ，原题计算错误，不合题意．
故选：C
【点睛】本题考查了去括号的法则．去括号时，括号前面是正号的，去掉括号后，括号里的各项都不变号；括号前面是负号的，去掉括号后，括号里的各项都变号．
6. 【答案】B
【解析】
【分析】
根据数轴上点的位置，结合相反数，绝对值的性质判断即可．
【详解】解：根据数轴上点的位置及，互为相反数，得，且，
则绝对值最大的是，
故选：B．
【点睛】此题考查了有理数与数轴，相反数，绝对值，熟练掌握各自的性质是解本题的关键．
7. 【答案】D
【解析】
【分析】
利用近似数的精确度逐项判断即可．
【详解】解：A.近似数5.1万精确到千位，此选项错误；
B.2.709精确到个位的近似数是3，此选项错误；
C.0.154精确到十分位为0.2，此选项错误；
D.近似数1.31×105精确到千位，此选项正确．
故答案为D．
【点睛】本题考查了近似数和有效数字，掌握确定有效数字的位数和精确的位数是解答本题的关键．
8. 【答案】A
【解析】
【分析】
根据绝对值的性质结合a+b>0得出a，b的取值情况，然后利用有理数减法法则计算.
【详解】解：∵|a|＝8，|b|＝5，
∴a＝±8，b＝±5，
又∵a＋b＞0，
∴a＝8，b＝±5．
当a＝8，b＝5时，a−b＝8－5＝3，
当a＝8，b＝－5时，a−b＝8－（－5）＝13，
∴a−b的值是3或13，
故选A．
【点睛】本题考查了绝对值的性质以及有理数的加减运算，此类题要注意答案一般有2个．两个绝对值条件得出的数据有4组，再添上a，b大小关系的条件，一般剩下两组答案符合要求，解此类题目要看清条件，以免漏掉答案或写错．
9. 【答案】A
【解析】
【分析】
根据关于的方程是—元—次方程，得到m-1≠0且，求出m即可．
【详解】解：因为关于的方程是—元—次方程，
所以m-1≠0且，
所以m=-1．
故选：A
【点睛】本题考查了一元一次方程的定义，熟知一元一次方程的定义是解题关键，要注意本题中m-1≠0这个条件．
10. 【答案】B
【解析】
【分析】
根据题中的规定判断出各选项的正确与否即可．
【详解】解：①若，即，
解得：，
则，符合题意；
②若，则，符合题意；
③若，则，即或，
解得：，即能使已知等式成立的x的值存在，不符合题意；
④式子的最小值是7，符合题意．
正确的所有结论是：①②④．
故选：B．
【点睛】此题考查了函数值，以及绝对值，弄清题中的新规定是解本题的关键．
二、填空题
11. 【答案】-3
【解析】
【分析】
首先审清题意，明确“正”和“负”所表示的意义；再根据题意作答．
【详解】解：∵水位升高3m时，水位变化记作+3m，
∴水位下降3m时，水位变化记作﹣3m．
故答案为﹣3．
【点睛】本题考查了正数和负数，解题关键是理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．在一对具有相反意义的量中，先规定其中一个为正，则另一个就用负表示．
12. 【答案】．
【解析】
【分析】
先比较两个负数的绝对值，再根据“两个负数比较大小，绝对值大的反而小”比较即可．
【详解】解：∵，
∴．
故答案为：．
【点睛】本题考查了比较两个数的大小，比较的原则是“正数大于0,0大于负数，两个负数比较大小，绝对值大的反而小”．
13. 【答案】
【解析】
【分析】
用珠穆朗玛峰的峰顶高度减去最低高度，再根据减去一个数等于加上这个数的相反数进行计算即可得解．
【详解】解：（米），
故答案为：．
【点睛】本题考查了有理数的减法，熟记减去一个数等于加上这个数的相反数是解题的关键．
14. 【答案】
【解析】
【分析】
根据绝对值和偶次方的非负性得到，，即可求解．
【详解】解：∵，
∴，，
即，，
∴，
故答案为：．
【点睛】本题考查绝对值和偶次方的非负性、有理数的乘方，根据绝对值和偶次方的非负性得到x和y的值是解题的关键．
15. 【答案】等式的性质2
【解析】
【分析】
根据5x=25得到x=-5，可以看出是在方程两边同时除以5，结果仍相等，据此判断即可．
【详解】解：由5x=25得到x=-5，其根据是等式的性质2，即等式的两边同时乘以一个数或除以一个不为0的数，结果仍相等．
故答案为：等式的性质2
【点睛】本题考查了解一元一次方程的依据，熟知等式的两个性质是解题的关键．
16. 【答案】10，6，1.8，0.16．
【解析】
【分析】
先根据输出结果为51列出一元一次方程，然后依次计算，直至x不是正数即可．
【详解】解：∵输出结果为51
∴5x+1=51，解得x=10＞0；
∴5x+1=10，解答x=1.8＞0；
∴5x+1=1.8，解答x=0.16＞0；
∴5x+1=0.16，解答x=-0.168＜0；
故x可取值为10，6，1.8，0.16．
故答案为10，6，1.8，0.16．
【点睛】本题考查了代数式求值、解一元一次方程，理解最后输出51的相应x不一定是第一次输入x的值是解答本题的关键．
17. 【答案】 (1). 甲 (2). 1250
【解析】
【分析】
分别求得三种促销方式的实际支付费用，然后对比即可解答.
【详解】解：甲店需实际支付费用为：50×25=1250元；
乙店需实际支付费用为：60×25×（1-16%）=1260元；
丙店需实际支付费用为：60×25÷100=15,15×15=225,1500-225=1275元
所以甲家店最省钱，需实际支付1250元.
故答案为甲，1250.
【点睛】本题考查了有理数混合运算的应用，灵活运用有理数混合运算解决实际问题成为解答本题的关键.
18. 【答案】2a
【解析】
【分析】
根据数轴判断出a、b、c的符号和绝对值的大小，根据绝对值的意义脱去绝对值，去括号合并同类项即可求解．
【详解】解：由数轴可得b＜a＜0＜c，且，
所以a+c＞0，b+c＜0，a+b＜0，
所以
=
=
=．
故答案为：2a
【点睛】本题考查了数轴上点的意义，绝对值的意义，去括号，合并同类项等知识，根据数轴上点的位置，判断出绝对值内的式子的符号是解题关键．
19. 【答案】510
【解析】
【分析】
类比于现在我们的十进制“满十进一”，可以表示满七进一的数为：千位上的数百位上的数十位上的数个位上的数．
【详解】解：孩子自出生后的天数是，
故答案为：510．
【点睛】本题是以古代“结绳计数”为背景，按满七进一计算自孩子出生后的天数，运用了类比的方法，根据图中的数学列式计算；本题题型新颖，一方面让学生了解了古代的数学知识，另一方面也考查了学生的思维能力．
20. 【答案】 (1). 71 (2). 45 (3). 84
【解析】
【分析】
（1）根据第行最后一数为，得出第一个数为，根据每行数的个数为1，3，5，的奇数列，即可得出数字个数为，即可求出第9行的行第7个数；
（2）根据，，可得2020在第45行，根据第45行数字个数为，通过计算即可得2020是表中第45行，第84个数．
【详解】解：（1）由题意知第行最后一数为，则第8行的最后一个数是64，
所以第9行第1个数是65，
所以第9行第7个数是71．
故答案为：71；
（2）由（1）知第行的最后一数为，
则第一个数为：，
第行共有个数；
因为，，
，
所以第45行有89个数，最后一个数是2025，
所以2020在第45行，第84个数．
故答案为：45，84．
【点睛】本题考查了数字的变化规律，解题的关键是通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题．
三、解答题
21. 【答案】（1）；（2）79；（3）；（4）
【解析】
【分析】
（1）直接利用有理数加减法法则计算即可求解；
（2）直接利用有理数乘除法法则和有理数的加法法则计算即可求解；
（3）先将除法转化为乘法，利用乘法交换律将小括号外面计算出来，然后利用乘法分配律计算即可求解；
（4）先计算有理数的乘方，然后利用有理数的运算法则计算即可．
【详解】解：（1）

；
（2）


；
（3）



；
（4）



．
【点睛】本题考查有理数的混合运算，掌握有理数的运算法则是解题的关键．
22. 【答案】（1）；（2）
【解析】
【分析】
（1）直接合并同类项即可求解；
（2）先去括号，然后再合并同类项即可求解．
【详解】解：（1）
；
（2）

．
【点睛】本题考查整式的加减，掌握去括号、合并同类项的方法是解题的关键．
23. 【答案】（1）；（2）．
【解析】
【分析】
根据解一元一次方程的一般步骤解方程即可．
【详解】解：（1）
移项得 ，
合并同类项得 ；
（2）
去分母得 ，
去括号得 ，
移项得 ，
合并同类项得 ，
系数化1得 ．
【点睛】本题考查了解一元一次方程，熟知解一元一次方程的一般步骤是解题的关键．
24. 【答案】，
【解析】
【分析】
先利用整式的加减法法则化简，再把，代入求解即可．
【详解】解：

，
当，时，原式．
【点睛】本题考查整式的化简求值，掌握整式的加减法法则是解题的关键．
25. 【答案】（1）；（2）1；（3），，，
【解析】
【分析】
（1）根据新定义可得，计算即可求解；
（2）根据题意可得，得到关于x的一元一次方程，求解即可；
（3）由题意可得，解得，根据是整数且k是整数，求解即可．
【详解】解：（1），
故答案为：；
（2）根据题意可得，
∵，
∴，
解得，
故答案为：1；
（3）∵，
整理可得，
∴，
∵是整数，k是整数，
∴或，
∴，，，．
【点睛】本题考查新定义问题，掌握解一元一次方程的方法是解题的关键．
26. 【答案】（1）5；（2）或6；（3）随着点的移动，的值不变．
【解析】
【分析】
（1）根据数轴上两点的距离公式计算便可．
（2）根据已知线段的关系式，列出绝对值方程进行解答即可．
（3）用点表示的数，列出关于的代数式进行讨论解答即可．
【详解】解：（1）点在数轴上对应的数为，点对应的数为2，
．
（2）存在．
设点对应的数为，解方程，得，
点对应的数为，
，
，即，，
①当时，有，解得；
②当时，有，此方程无解；
③当时，有，解得；
综上，点的对应数为或6．
（3）设点对应的数为，则，，
若点是数轴上在点左侧的一点，线段的中点为点，点为线段的三等分点且靠近于点，
，则点对应的数为；，则点对应的数为；
，则．
随着点的移动，的值不变．
【点睛】本题是数轴的一个综合题，涉及一元一次方程的应用，两点距离公式，利用绝对值的性质化简绝对值代数式是解题的关键．
B卷
27. 【答案】 (1). 3 (2). 5
【解析】
【分析】
（1）用“正”表示杯口朝上，用“负”表示杯口朝下，根据翻转要求逐步罗列即可得；
（2）用“正”表示杯口朝上，用“负”表示杯口朝下，根据翻转要求逐步罗列即可得．
【详解】（1）用“正”表示杯口朝上，用“负”表示杯口朝下，
刚开始时：正、正、正、正、正，
第一次翻转结束后：负、负、负、正、正，
第二次翻转结束后：负、正、正、负、正，
第三次翻转结束后：负、负、负、负、负，
则m的最小值为3；
（2）用“正”表示杯口朝上，用“负”表示杯口朝下，
刚开始时：正、正、正、正、正、正、正、正、正、正、正，
第一次翻转结束后：负、负、负、正、正、正、正、正、正、正、正，
第二次翻转结束后：负、负、负、负、负、负、正、正、正、正、正，
第三次翻转结束后：负、负、负、负、负、负、负、负、负、正、正，
第四次翻转结束后：负、负、负、负、负、负、负、正、正、负、正，
第五次翻转结束后：负、负、负、负、负、负、负、负、负、负、负，
则n的最小值为5；
故答案：3，5．
【点睛】本题考查了相反意义的量，正确罗列翻转后杯口的变化情况是解题关键．
28. 【答案】 (1). (2).
【解析】
【分析】
根据题意，任意四个相邻格子中的和等于15，即4个数为1组循环，根据规律列出等式，计算出的值；再求出第2021个数是几即可．
【详解】解：任意四个相邻格子中的和等于15，即4个数为一组循环，
所以第3个数、第5个数、第16个数、第78个数分别对应一组循环中的第3个数、第1个数、第4个数、第2个数，
∴根据题意得：，
解得，
则，
，
第2021个数是．
故答案为：；．
【点睛】本题主要考查数字的变化规律，解决此题的关键是根据题意，列出等式，求出字母的值．
29. 【答案】 (1). 64 (2). 54
【解析】
【分析】
根据依次先减少三分之一，后增加三分之一，列式计算可求第五个基准音的乐器的长度；再依此根据能发出第四个基准音的乐器的长度是32，列出方程可求的值．
【详解】解：第五个基准音的乐器的长度为：

；
依题意有，
解得．
故第五个基准音的乐器的长度为64，的值是54．
故答案为：64，54．
【点睛】考查了有理数的混合运算，关键是找到规律，正确列式计算即可求解．
30. 【答案】（1）填表见解析；（2）答案见解析
【解析】
【分析】
（1）根据“异或”运算的定义填写表格即可；
（2）根据字母“”的编码排布、运算及二维码填涂即可求解．
【详解】解：（1）填表如下：
a
b
结果
0
0
0
1
0
1
0
1
1
1
1
0
（2）“”的编码排布、运算及二维码填涂如下：

【点睛】本题考查新定义问题，理解题意是解题的关键．