专题12 三角形与全等三角形——2023年河南省中考数学模拟题分项选编

2023年河南省中考数学模拟题分项选编

专题12  三角形与全等三角形

一、单选题

1．（2023·河南洛阳·统考一模）如图，直线，点B在a上，那么等于（　　）

A． B． C． D．

2．（2023·河南郑州·统考二模）如图，一副三角尺按如图所示的方式放置，若，则的度数为（　　）

A． B． C． D．

3．（2023·河南安阳·统考二模）如图，在中，是的平分线，过点的射线与平行，若，，则的度数为（　　）

A． B． C． D．

4．（2023·河南驻马店·统考二模）如图，直线，一副三角板的顶点A，C分别在b，a上，若，则的度数为（　　）

A． B． C． D．

5．（2023·河南开封·统考一模）如图，已知，若，，则为（　　）

A． B． C． D．

6．（2023·河南南阳·统考一模）如图所示，的一边为平面镜，，一束光线（与水平线平行）从点C射入经平面镜上的点D后，反射光线落在上的点E处，则的度数是（　　）

A． B． C． D．

7．（2023·河南安阳·统考二模）如图，，点D在上，，则的度数为（　　）

A． B． C． D．

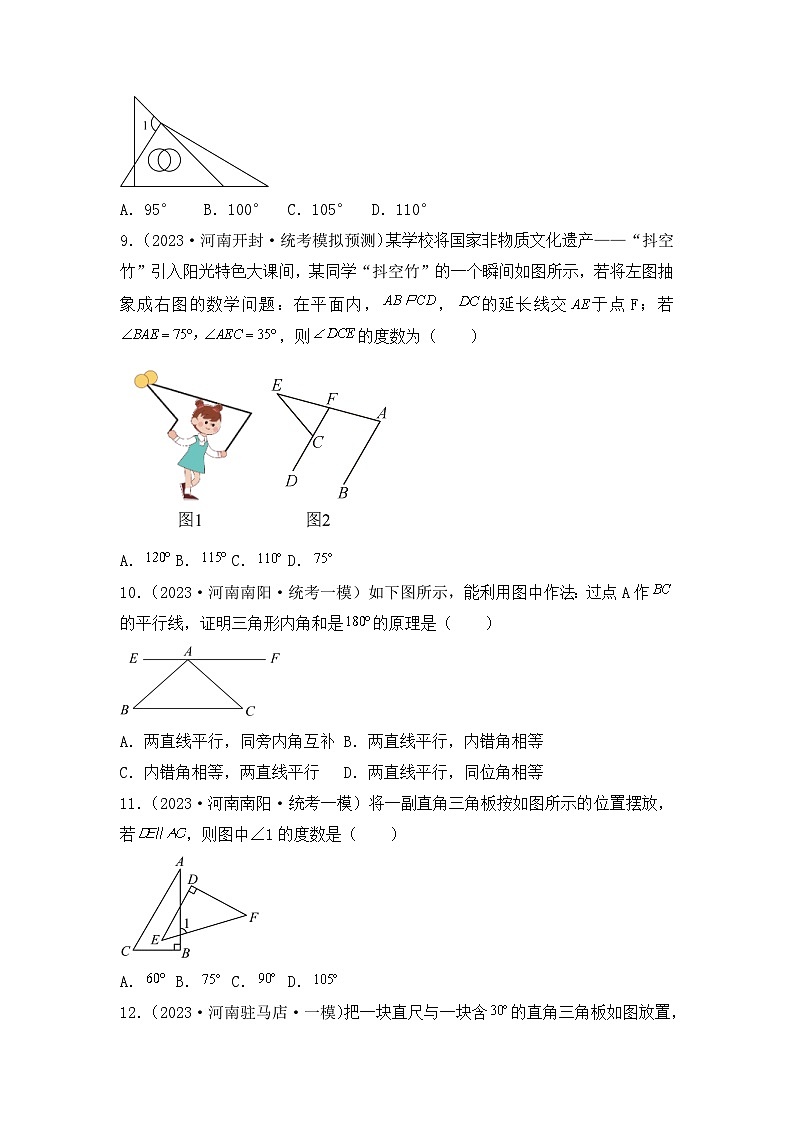
8．（2023·河南商丘·统考三模）将一副三角板如图放置，则的度数是（　　）

A．95° B．100° C．105° D．110°

9．（2023·河南开封·统考模拟预测）某学校将国家非物质文化遗产——“抖空竹”引入阳光特色大课间，某同学“抖空竹”的一个瞬间如图所示，若将左图抽象成右图的数学问题：在平面内，，的延长线交于点F；若，则的度数为（　　）

A． B． C． D．

10．（2023·河南南阳·统考一模）如下图所示，能利用图中作法：过点A作的平行线，证明三角形内角和是的原理是（　　）

A．两直线平行，同旁内角互补 B．两直线平行，内错角相等

C．内错角相等，两直线平行 D．两直线平行，同位角相等

11．（2023·河南南阳·统考一模）将一副直角三角板按如图所示的位置摆放，若，则图中∠1的度数是（　　）

A． B． C． D．

12．（2023·河南驻马店·一模）把一块直尺与一块含的直角三角板如图放置，若，则的度数为（　　）

A． B． C． D．

13．（2023·河南商丘·统考一模）如图，直线a//b，Rt△ABC 如图放置，若∠1=28°，∠2=80°，则∠B的度数为( )

A．62° B．52° C．38° D．28°

14．（2023·河南周口·统考一模）如图，AB∥CD，∠1＝30°，∠2＝40°，则∠3的度数为（　　）

A．50° B．60° C．70° D．80°

15．（2023·河南开封·统考一模）小明同学为某机器人编制一段程序，如果机器人在平地上按照图中所示的步骤行走，那么该机器人所走的总路程为（　　）

A．24米 B．20米 C．15米 D．不能确定

16．（2023·河南新乡·统考一模）如图，已知a∥b，含30°角的直角三角板的顶点在直线b上，若∠1＝24°，则∠2等于（　　）

A．110° B．112° C．114° D．120°

17．（2023·河南三门峡·统考一模）如图，在和中，点A、E、B、D在同一条直线上，，，只添加一个条件，不能判断的是（　　）

A． B． C． D．

18．（2023·河南南阳·统考二模）如图，平分，点是射线，上的点，连接．按以下步骤作图：

①以点为圆心，任意长为半径作弧，交于点，交于点；

②分别以点和点为圆心，大于长为半径作弧，两弧相交于点；

③作射线，交于点．若，，则的度数为（　　）

A． B． C． D．

19．（2023·河南濮阳·统考二模）如图，直线，点、分别在、上，以点为圆心，适当长为半径画弧，交、于点、；分别以、为圆心，大于长为半径画弧，两弧交于点；作射线交于点．若，则的度数为（　　）

A． B． C． D．

20．（2023·河南开封·统考模拟预测）如图，在中，，，以为圆心，任意长为半径画弧分别交、于点和，再分别以、为圆心，大于的长为半径画弧，两弧交于点，连接并延长交于点，以下结论错误的是（　　）

A．是的平分线 B．

C．点在线段的垂直平分线上 D．

21．（2023·河南郑州·二模）如图，在中，，．以点A为圆心，以任意长为半径作弧交于D，E两点；分别以点D，E为圆心，以大于长为半径作弧，在内两弧相交于点P；作射线交于点F，过点F作，垂足为G．若，则的周长等于（　　）

A．  B． C．  D．

二、填空题

22．（2023·河南南阳·统考一模）用一根小木棒与两根长分别为、的小木棒围成三角形，则这根小木棒的长度可以为__________（写出一个即可）

23．（2023·河南信阳·校考一模）如图，在△ABC中，AD⊥BC， CE⊥AB，垂足分别是D，E．AD，CE交于点H，已知AE＝CE＝5，CH＝2，则BE＝__________．

三、解答题

24．（2023·河南郑州·统考二模）下面是小颖同学要借助无刻度的直尺和圆规作图，来证明三角形内角和等于这一命题，请你帮她补充完整．

25．（2023·河南驻马店·统考一模）如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，BE，点P为DC的中点，

（1）【观察猜想】图1中，线段AP与BE的数量关系是 ，位置关系是 ．

（2）【探究证明】把△ADE绕点A逆时针旋转到图2的位置，（1）中的猜想是否仍然成立？若成立请证明，否请说明理由；

（3）【拓展延伸】把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出线段AP长度的最大值和最小值．

26．（2023·河南南阳·模拟预测）（1）问题发现：如图1，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，则AB，AD，DC之间的数量关系为_______．

（2）问题探究：如图2，在四边形ABCD中，AB∥DC，E是BC的中点，点F是DC的延长线上一点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的数量关系，并证明你的结论；

（3）问题解决：如图3，AB∥CD，点E在线段BC上，且BE:EC=3:4．点F在线段AE上，且∠EFD =∠EAB，直接写出AB，DF，CD之间的数量关系．

参考答案

1．C

【分析】根据平行线的性质得出，根据，得出，最后求出结果即可．

【详解】解：∵，，

∴，

∵，

∴，

∴．

故选：C．

【点睛】本题主要考查了平行线的性质，垂线定义，直角三角形两锐角互余，对顶角相等，解题的关键是熟练掌握平行线的性质求出．

2．C

【分析】由三角板的特点可知，．根据平行线的性质可得出，最后由三角形外角的性质求解即可．

【详解】解：由三角板的特点可知，．

∵，

∴，

∴．

故选C．

【点睛】本题考查三角板中的角度计算，平行线的性质，三角形外角的性质．利用数形结合的思想是解题关键．

3．B

【分析】根据三角形内角和定理求出，再根据角平分线的定义可得，最后利用平行线的性质可得．

【详解】解：，，

，

是的平分线，

，

，

，

故选：B．

【点睛】本题考查三角形内角和定理，角平分线的定义，平行线的性质．熟练掌握平行线的性质是解题的关键．

4．B

【分析】根据平行线的性质，互余的性质计算即可．

【详解】∵直线，，

∴，

∵，

∴，

故选B．

【点睛】本题考查了平行线的性质，互余的性质，熟练掌握平行线的性质是解题的关键．

5．C

【分析】根据平行线的性质可得，结合三角形外角的性质可得的度数．

【详解】解：∵，

∴，

又∵，，

∴，

故选：C．

【点睛】本题考查了平行线的性质和三角形外角的性质，掌握同一平面内，两直线平行，内错角相等，和三角形的外角等于与它不相邻的两个内角的和是解答本题的关键．

6．B

【分析】根据平行线的性质，得到，根据反射，得到，利用外角的性质，即可得出结果．

【详解】解：∵，

∴，

∵反射，

∴，

∴；

故选B．

【点睛】本题考查平行线的性质，三角形外角的性质．熟练掌握入射光线与镜面的夹角，等于反射光线与镜面的夹角，是解题的关键．

7．C

【分析】延长交于点E，根据直角三角形两锐角互余及对顶角相等即可得到答案；

【详解】解：延长交于点E，如图所示，

∵，

∴，

∴，

∴，

故选：C．

【点睛】本题考查直角三角形两锐角互余，对顶角相等，掌握直角三角形两锐角互余是解题的关键．

8．C

【分析】根据三角形外角的性质结合三角板中角度的特点进行求解即可．

【详解】解：由题意得，，

∴，

故选：C．

【点睛】本题主要考查了三角形外角的性质，三角板中角度的计算，熟知三角形一个外角的度数等于与其不相邻的两个内角度数之和是解题的关键．

9．C

【分析】根据平行线的性质得到，根据三角形外角性质求解即可．

【详解】解：∵，，

∴，

∵，

∴，

故选：C．

【点睛】此题考查了平行线的性质和三角形外角的性质，熟记“两直线平行，同位角相等”是解题的关键．

10．B

【分析】根据题意得，，则，，根据平角的性质得，即可得．

【详解】解：根据题意得，，

∴，，

∵，

∴，

故选：B．

【点睛】本题考查了平行线的性质，掌握“两直线平行，内错角相等”是解决本题的关键．

11．B

【分析】根据平行线的性质，可得，再利用三角形的外角性质即可求出结论．

【详解】解：如图所示：与相交于点G，，

，

，

，

，

故选：B．

【点睛】本题考查的是平行线的性质，三角形的外角性质，解题的关键是熟练掌握相关的性质．

12．B

【分析】根据平行线的性质和三角形外角的性质解答即可．

【详解】如图，

由题意可知，

∴．

∵，

∴．

故选B．

【点睛】本题考查三角板中的角度计算，平行线的性质，三角形外角的性质．掌握三角形的一个外角等于与它不相邻的两个内角和是解题关键．

13．C

【分析】如图：根据两直线平行、同位角相等可得∠1+∠3=∠2，进而求得∠3，再根据直角三角形的性质求得∠B即可．

【详解】解：如图，∵ab,

∴∠1+∠3=∠2，

∵∠3=∠2-∠1=80°-28°=52°，

∵∠ACB=90°，

∴∠B+∠3 =90°，

∴∠B=90°-52°=38°．

故答案为：C．

【点睛】本题主要考查了平行线的性质、直角三角形的性质等知识点，灵活应用平行线的性质成为解答本题的关键．

14．C

【分析】利用平行线的性质：两直线平行，内错角相等，得出∠A和∠1相等，再利用三角形外角的性质即可求出答案．

【详解】解：∵AB∥CD，∠1＝30°，

∴∠A＝∠1＝30°，

又∠2＝40°，

∵∠3＝∠A+∠2＝70°，

故选：C．

【点睛】本题考查的是平行线的性质及三角形外角的性质，牢固掌握以上知识点是做出本题的关键．

15．A

【分析】先判断出机器人所走过的路线是正多边形，然后用多边形的外角和除以每一个外角的度数求出多边形的边数，再根据周长公式列式进行计算即可得解．

【详解】解：根据题意得，机器人所走过的路线是正多边形，

每一次都是左转，

多边形的边数，

周长米；

故选：A．

【点睛】本题考查了多边形的内角与外角，判断出走过的路线是正多边形是解题的关键．

16．C

【分析】由题意可求得∠DBC＝54°，再由平行线的性质可求得∠3＝126°，再利用四边形的内角和为360°即可求得∠2的度数．

【详解】解：如图，

由题意得∠DBC＝∠1+30°＝54°，

∵ab，

∴∠DBC+∠3＝180°，

∴∠3＝180°﹣∠DBC＝126°，

∵∠A＝90°，

∴∠2＝360°﹣∠90°﹣30°﹣126°＝114°．

故选：C．

【点睛】本题主要考查平行线的性质和四边形的内角和360°，解答的关键是熟记平行线的性质：两直线平行，同旁内角互补．

17．C

【分析】先证明，再根据三角形全等的判定方法做出选择即可．

【详解】解：∵，

∴，

A、，， 能判断，选项不符合题意；

B、，利用AAS可以判断，不选项符合题意；

C、，不能判断，选项符合题意；

D、，能判断，选项不符合题意；

故选：B．

【点睛】本题考查三角形全等的判定，根据、、、、判断三角形全等，找出三角形全等的条件是解答本题的关键．

18．B

【分析】根据条件可知平分，则可求出，根据平分求出，进而利用即可求出答案．

【详解】由作法得平分，

∴，

∵平分，

∴，

∵，

∴．

故选B．

【点睛】本题主要考查角平分线的定义及作法，三角形的外角的性质，根据题目条件发现角平分线是解题的关键．

19．B

【分析】根据作图可知是的角平分线，进而根据平行线的性质即可求解．

【详解】解：∵，

∴

∵，

∴

根据作图可知是的角平分线，

∴，

故选：B．

【点睛】本题考查了作角平分线，平行线的性质，熟练掌握基本作图是解题的关键．

20．D

【分析】由作图可得：平分 可判断A，再求解 可得 可判断B，再证明 可判断C，过作于 再证明 再利用 ，可判断D 从而可得答案．

【详解】解：

由作图可得：平分 故A不符合题意；

故B不符合题意；

在的垂直平分线上，故C不符合题意；

过作于

平分

故D符合题意；

故选：D．

【点睛】本题考查的是三角形的内角和定理，角平分线的作图，角平分线的性质，线段垂直平分线的判定，等腰三角形的判定，掌握以上知识是解题的关键．

21．B

【分析】由角平分线的性质，得到，由证明，得到，然后求出的周长即可．

【详解】解：由作图知，是的平分线，

∵，，

∴，

在和中，，

∴，

∴，

在中，，，

∴的周长为：

；

故选：B．

【点睛】本题考查了角平分线的性质，全等三角形的判定和性质，解题的关键是掌握角平分线的性质．

22．（答案不唯一）

【分析】根据在三角形中任意两边之和大于第三边，任意两边之差小于第三边，即可求第三根木条的取值范围．

【详解】解：设这根木棒长为，

∵这根木棒与两根长分别为、的小木棒围成三角形，

∴，即，

即的取值范围是，在这一范围内任意长度都可以．

故答案为：（答案不唯一）．

【点睛】本题考查三角形三边关系，实际上就是根据三角形三边关系定理列出不等式，然后解不等式，确定取值范围即可．掌握三角形三边关系定理是解题的关键．

23．3

【分析】由AD垂直于BC，CE垂直于AB，利用垂直的定义得到一对角为直角，再由一对对顶角相等，利用三角形的内角和定理得到一对角相等，再由一对直角相等，以及一对边相等，利用AAS得到△AEH与△EBC全等，由全等三角形的对应边相等和线段的和差即可得出结论．

【详解】解：∵AD⊥BC，CE⊥AB，

∴∠ADB=∠AEH=90°，

∵∠AHE=∠CHD，

∴∠BAD=∠BCE，

∵在△HEA和△BEC中，

∴△HEA≌△BEC（AAS），

∴BE=EH，

∵AE＝CE＝5，CH＝2，

∴BE=EH=CE-CH=3，

故答案为：3．

【点睛】此题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定与性质是解本题的关键．

24．见解析

【分析】先根据作与已知角相等的角的尺规作图方法作图，然后根据证明，得到，由平角的定义可得∠，则．

【详解】证明：如图，

∵，

∴，

∴，

∵∠，

∴，

即三角形三个内角的和等于．

【点睛】本题主要考查了三角形内角和的证明，平行线的性质，尺规作图—作与已知角相等的角，灵活运用所学知识是解题的关键．

25．（1）AP＝BE，PA⊥BE；（2）成立，理由见解析；（3）PA的最大值为7，最小值为3

【分析】(1)设PA交BE于点O，根据题目已知条件可以得到△DAC≌△EAB，从而得出PA＝BE，∠C＝∠PAE，因为∠CAP+∠BAO＝90°，即可证明出结论；

(2)结论成立，延长AP至M，使PM＝PA，连接MC，延长PA交BE于O，根据题目已知条件得出△APD≌△MPC，进而得到∠EAB＝∠ACM，再证明得出△EAB≌△MCA，即可得出结论；

(3)因为AC＝10，CM＝4，所以6≤AM≤14，再利用AM＝2AP即可得出答案．

【详解】解：(1)设PA交BE于点O，

∵AD＝AE，AC＝AB，∠DAC＝∠EAB，

∴△DAC≌△EAB，

∴BE＝CD，∠ACD＝∠ABE，

∵∠DAC＝90°，DP＝PC，

∴PA＝CD＝PC＝PD，

∴PA＝BE，∠C＝∠PAE，

∵∠CAP+∠BAO＝90°，

∴∠ABO+∠BAO＝90°，

∴∠AOB＝90°，

∴PA⊥BE，

(2)结论成立．

理由：延长AP至M，使PM＝PA，连接MC，延长PA交BE于O，

∵PA＝PM，PD＝PC，∠APD＝∠CPM，

∴△APD≌△MPC，

∴AD＝CM，∠ADP＝∠MCP，

∴AD∥CM，

∴∠DAC+∠ACM＝180°，

∵∠BAC＝∠EAD＝90°，

∴∠EAB＝∠ACM，

∵AB＝AC，AE＝CM，

∴△EAB≌△MCA，

∴BE＝BM，∠CAM＝∠ABE，

∵PA＝AM，PA＝BE，

∵∠CAM+∠BAO＝90°，

∴∠ABE+∠BAO＝90°，

∴∠AOB＝90°，

∴PA⊥BE．

(3)∵AC＝10，CM＝4，

∴10﹣4≤AM≤10+4，

∴6≤AM≤14，

∵AM＝2AP，

∴3≤PA≤7．

∴PA的最大值为7，最小值为3．

【点睛】本题主要考查的是全等三角形综合应用，掌握全等三角形的判定，三角形的构成条件是解题的关键．

26．（1）AB+CD=AD；（2）详见解析；（3）AB=(CD+DF ) ．

【分析】（1）结论：AB+CD=AD．只要证明△CEF≌△BEA（AAS），推出AB=CF，再证明DA=DF即可解决问题．

（2）结论：AB=AF+CF．只要证明△CEG≌△BEA（AAS），推出AB=CG，再证明FA=FG即可解决问题．

（3）结论：AB=（CD+DF）．如图3中，延长AE交CD的延长线于G．证明△CEG∽△BEA，推出AB=CG，再证明DF=DG即可解决问题．

【详解】（1）结论：AB+CD=AD．

理由：如图1中，

∵AB∥CF，∴∠CFE=∠EAB，

∵CE=EB，∠CEF=∠AEB，∴△CEF≌△BEA（AAS），

∴AB=CF．

∵AF平分∠DAB，∴∠DAF=∠EAB，

∵∠EAB=∠CFE，∴∠DAF=∠DFA，

∴AD=DF，

∵DF=DC+CF=CD+AB，

∴AB+CD=AD．

故答案为 AB+CD=AD．

（2）结论：AB=AF+CF

延长AE交DC的延长线于点G．

∵AB∥CD，∴∠EAB=∠G， ∠B=∠BCG．

又E是BC的中点， ∴BE=CE．

∴△ABE≌△GCE，∴AB=CG．

∵AE是∠BAF的平分线，

∴∠EAB=∠FAE， ∴∠G=∠FAE．

∴AF=FG， ∴CG=CF+FG= CF+AF．

∴AB=AF+CF．

（3）结论：AB=(CD+DF ) ．

如图3中，延长AE交CD的延长线于G．

∵CG∥AB，

∴△CEG∽△BEA，

∴ ，

∵∠G=∠A，

∴AB=CG，

∵∠DFE=∠A，

∴∠DFG=∠G，

∴DF=DG，

∴CD+DF=CD+DG=CG，

∴AB=（CD+DF）．

【点睛】本题属于四边形综合题，考查的是全等三角形的判定和性质、相似三角形的判定和性质，准确识图是解题的关键.