2023年江苏省盐城市鹿鸣路初级中学中考一模数学试题

这是一份2023年江苏省盐城市鹿鸣路初级中学中考一模数学试题，共8页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

初三数学试卷
（卷面总分：150分 光时间：120分钟）
命题人:孔桦为 蔡旭照 审核人:谢射红 陈晓红
一、选择题（本大题共有8小题，每小题3分，共24分.在每小随所给出的四个选项中，只有一项提解合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）
1. -2023的绝对值是 （ ▲ ）
A. B.2023 C. - 2023 D.
2.下列图形是中心对称图形的是（ ▲ ）
3.已知sin α＝32，则锐角α的度数等于（ ▲ ）
A.30° B.45° C.60° D.30°或60°
4.如右图，⊙O的半径为5，弦AB＝8，OC⊥AB于点C，则OC的长为（ ▲ ）
A.1 B.2 C.3 D.4
5.如图是由5个完全相同的正方体搭成的几何体，这个儿何体的出视图是 （ ▲ ）
6.墨迹覆盖了等式 －（x2+ 1）＝3x中的多项式，则覆盖的多项式为（ ▲ ）
A、x+2 B. -x2+3x－1 C. - x2+3x+1 D. x2+3x+1
7.近日，杭州亚运会游泳选拔赛已开赛，其中参加男子100米自由泳的甲、乙、丙、丁四位运动员的5次比赛的平均成绩x-和方差S2如表所示:
若要选拔一名速度快且发挥稳定的运动员参加亚运会集训营，根据表中数据应选择（▲）
A.甲 B.乙 C.丙 D.丁
8.如图，在△ABC中，已知AC＝BC＝2. ∠ACB＝90°，点P是线段AB上的动点，连接CP，在CP上有一点M，始终保持∠ACP＝∠CBM，连接AM，则AM的最小值为（ ▲ ）
A.2 B.5-1 C.3-1 D.3
A
P
C B
第4题 第8题 第11题
二、填空题（本大题共有8小题，每小题3分，共24分.不需写出解答过程，请将答案直接写在答题卡相应位置上）
9. 因式分解:x2-1= ▲ _
10. 2023年五一假口期间，全国出游约274000000人次，同比增长70.83%.数据2740000000用科学记数法表示为 ▲ .
11. 如图，在△ABC中，D是BC的中点，点G是△ABC的重心.AD＝6，则AG＝__ ▲ ___.甲
乙
丙
丁
x- (秒)
48.67
49.05
48.67
49.03
S2(秒2)
0.03
0.07
0.06
0.04
12.设x1、x2，足方程x2-3x+2＝0的两个根，则x1+x1＝ ▲ .
13.如图，点A、B、C、D在⊙O上，∠AOC＝130°.则∠ABC＝ ▲ .
14.如果所示的地板由15块方砖组成，每一块方砖除颜色外完全相同，小球在这块地板上自由滚动，随机停在黑色方砖的概率为 ▲ .
15.小明参加“强国有我”主题演讲比赛，其演讲形象、内容、效果三项的成绩分别是70分、90分、80分.若将三项得分依次按2 : 4 : 4的比例确定最终成绩，则小明的最终比赛成绩为 ▲ .分.
16.已知△ABC，动点P从点A出发，以每秒钟1个单位长度的速度沿A→B→C→A方向运动到点A处停止.设点P运动的运动时间为t秒，△PAB的面积S关于t的函数图像如图所示，则△ABC的边BC上的高等于 ▲ .
三、解答题（本大题共有11小题，共102分.请在答题卡指定区域内作答，解答时应写出文字说明、理过程或演算步骤）
17.（6分）计算:（13）-1- 2cs45°+|1-2|
18.（6分）解不等式 12（x-1）＜52-x，并把不等式的解集在数轴上表示出来.
19.（8分）先化简，再求值:（1-1a）÷a2-1a，其中a＝-23
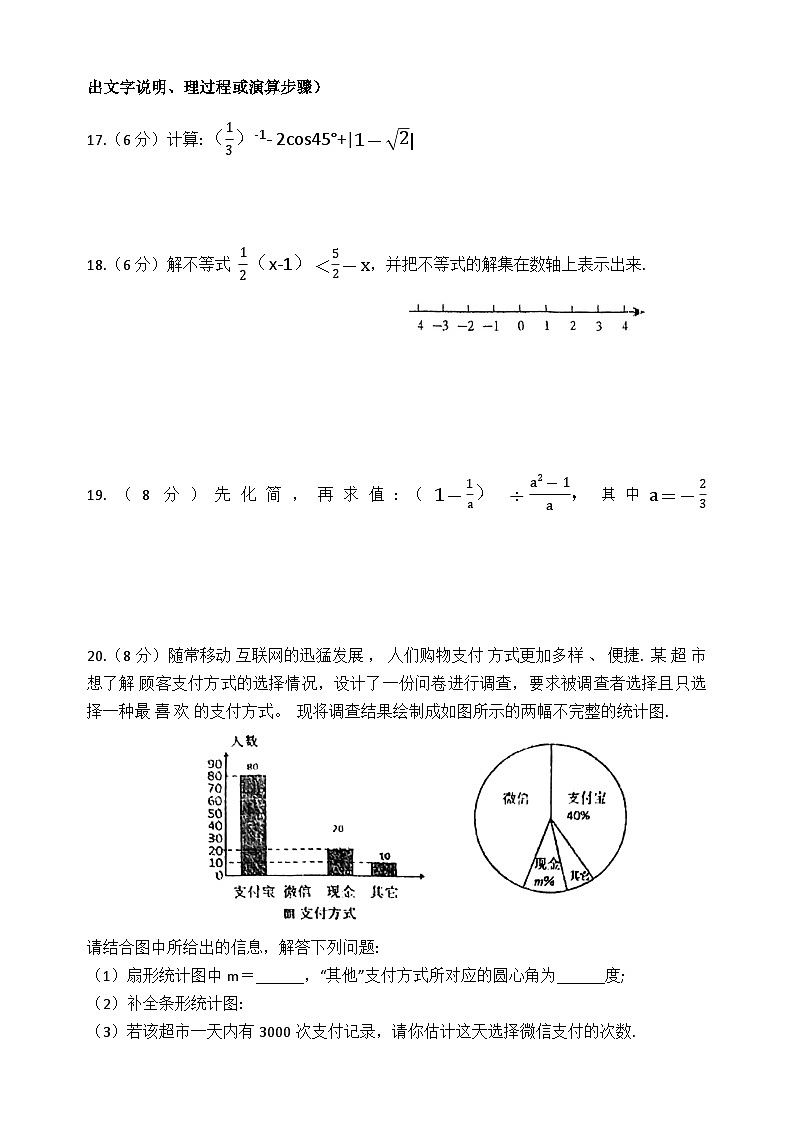
20.（8分）随常移动 互联网的迅猛发展 ， 人们购物支付 方式更加多样 、 便捷. 某 超 市 想了解 顾客支付方式的选择情况，设计了一份问卷进行调查，要求被调查者选择且只选择一种最 喜 欢 的支付方式。 现将调查结果绘制成如图所示的两幅不完整的统计图.
请结合图中所给出的信息，解答下列问题:
（1）扇形统计图中m＝______，“其他”支付方式所对应的圆心角为______度;
（2）补全条形统计图:
（3）若该超市一天内有3000次支付记录，请你估计这天选择微信支付的次数.
21.（8分）为了切实帮助家长解决在学生教育上的困惑，学校举办了一场家庭教育沙龙并邀请了部分家长参加活动。在场地安排了9把椅子（每个方格代表一把椅子，横为排，竖为列）按图示方式摆放，其中圆点表示已经有家长入座的椅子.
（1）如图① ，已经有两位家长入座，又有一位家长随机入座，则这三把椅子刚好在同一直线上的概率为______;
（2）如图② ，已经有四位家长入座四个位置，又有甲、乙两位家长随机入座，已知甲坐第一排，乙坐第二排，用树状图或列表法求甲，乙两人刚好坐在同一列上的概率.
22.（10分）如图，已知一次函数y1＝k1x + b的图像与反比圆叫数y2= k2x，分别交于点A 和点B，且A、B两点的坐标分别是A（-1，-2）和B（2.m），连接OA、OB.
（1）求一次函数y1＝k1x+b与反比例币数y2＝k2x的函数表达式:
（2）求△AOB的面积.
23.（10分）（1）如图，A、B两点分别位于一个池塘的两端，小聪想要测量A、B间的距离，一位同学帮他想了一个办法:先在地上取一个可以直接到达A、B的点O，分别延长AO、BO至点M、N，使得MO=AO，NO＝BO，再连接MN，则MN的长度即为池塘A、B间的距离.请说明理由.
（2）在右面的网格图中有三个点A、B、D，其中点A和点D在网格线的交点处，点B在网格线上，请找出点C，使得四边形ABCD是平行四边形.（仅用无刻度的直尺作图，保留作图痕迹，不需说明理由）
24.（10分）《海岛算经》是我国魏晋时期的著名数学家刘徽所撰，该书研究的对象全是有关高与距离的测量，因首题测算海岛的高、远，故而书名由此而来，它是中国最早的一部测量数学著作，亦为地图学提供了数学基础。书中第四题为:今有望深谷，偃距岸上，令勾高六尺，从勺端望谷底，入下股九尺一寸， 又设重矩于上，其矩间相去三丈（30尺），更从勺端望谷底，入上股八尺五寸，问谷深几何？大致译文如下:现在要测量谷的深度AK，拿一个高AG为6尺的“矩尺”（∠GAH）仰放在岸上，从G处望向谷底LK（H在LG上），下股AH为9.1尺，在KA的延长线上重新放置“矩尺”（∠EBC），其中BE＝AG=6尺，AB＝30尺，从E处望向谷底LK（C在LE上），下股BC为8.5尺，求谷AK的深度.（已知∠GAH=90° ∠EBC＝90°、∠AKL＝90°）
25.（10分）如图，已知在△ABC中，AB＝AC，以AC为直径的⊙O分别交AB，BC于D，E两点，BF⊥CF于点F,且BF＝BD.
（1）求证:FC是⊙O的切线.
（2）若BF＝1. CE＝32，求⊙O的半径.
26.（12分）“鹿鸣·博约”数学兴趣小组开展了《再探矩形的折叠）这一课题研究.已知矩形ABCD，点E、F分别是AB、CD边上的动点.
（1）若四边形ABCD是正方形，如图① ，将四边形BCFE沿EF翻折，点B，C的对应点分别为M、N. 点M恰好是AD的中点.
① 若AD＝8，求AE的长度:
M
A D
E
G

N
F
B C
② 若MN与CD的交点为G,连接EG,试说明AE+DG＝EG.
（2）若AB＝23，AD＝2，如图② ，且AE＝CF，将四边形BCFE沿EF翻折，点B、C的对应点分别为B′、C′.当点E从点A运动至点B的过程中，点B′的运动路径长为_________.
A D
C’
F
B’

E
B C
（3）若四边形ABCD是正方形，如图③ ，连接DE交AC于点M，以DE为直径作圆，该圆与AC交于点A和点N.将△EMN沿EN翻折，若点M的对应点M′刚好落在BC边上，求此时AE的长度.
A D
MM
MM
E
B C
（14分）【定义】在平面直角坐标系中，有一条直线x＝m，对于任意一个函数图像，把该图像在直线x＝m上的点以及直线x＝m右边的部分向上平移n个单位长度
（n＞0），再把直线x＝m左边的解分向下平移n个单位长度，得到一个新的函数图像，则这个新函数叫做原函数关于直线x＝m的“n分移函数”。例如:函数y＝x关于直线x＝0的“1分移函数”为y＝x+1（x≥0）x-1（x＜0）·
【概念理解】
① 已知点P1（3，3）、P2（3，4）、P3（0，- 4），其中在函数y＝x-2关于直线
x＝2的“2分移函数”图像上的点有_________ ;
② 已知点M（3，4）在函数y＝kx（k≠0）关于直线x＝2的“1分移函数”图像上，求k的值.
【拓展探究】
（2）若二次函数y＝-x2+2x+6关于直线x＝3的“n分移函数”与x轴有三个公共点，是否存在n，使得这三个公共点的横坐标之和为3+23，若存在请求出n的值，若不存在，请说明理由.
【深度思考】
（3）已知A（-12，0），B（0，2），C（4，0），D（0，- 2），若函数y＝x2- bx（b＞0）关于直线x＝0的“3分移函数”图像与四边形ABCD的边恰好有4个公共点，请直接写出b的取值范围.