2023年广东省东莞市中考数学二模试卷（含解析）

2023年广东省东莞市中考数学二模试卷

学校:___________姓名：___________班级：___________考号：___________

第I卷（选择题）

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

1.  下列实数是无理数的是(    )

A.  B.  C.  D.

2.  某种芯片每个探针单元的面积为，用科学记数法可表示为(    )

A.  B.  C.  D.

3.  下列立体图形中，俯视图是三角形的是(    )

A.  B.  C.  D.

4.  下列计算正确的是(    )

A.  B.  C.  D.

5.  一个多边形的每个外角都等于，则这个多边形的边数为(    )

A.  B.  C.  D.

6.  把抛物线向左平移个单位，然后向下平移个单位，则平移后抛物线的解析式为(    )

A.  B.
C.  D.

7.  如图，，若，则的大小为(    )

A.
B.
C.
D.

8.  在同一平面直角坐标系中，一次函数与反比例函数的图象如图所示，则当时，自变量的取值范围为(    )

A.
B.
C.
D.

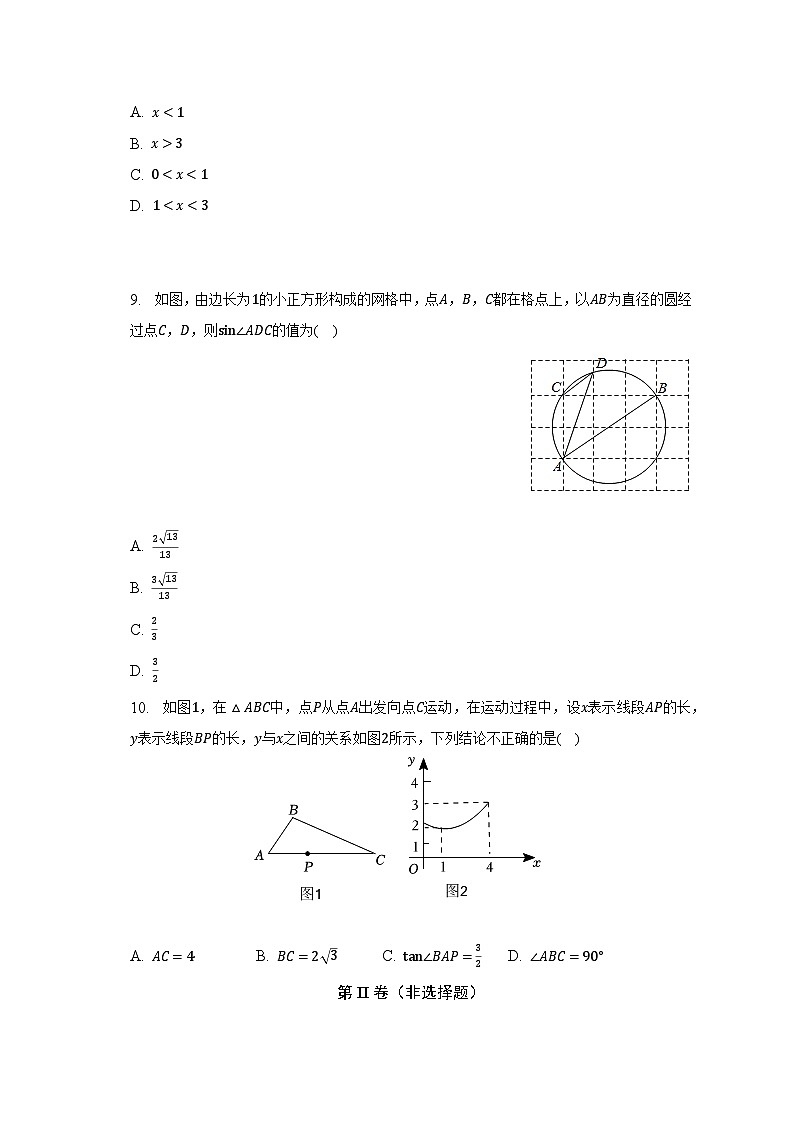
9.  如图，由边长为的小正方形构成的网格中，点，，都在格点上，以为直径的圆经过点，，则的值为(    )
 

A.
B.
C.
D.

10.  如图，在中，点从点出发向点运动，在运动过程中，设表示线段的长，表示线段的长，与之间的关系如图所示，下列结论不正确的是(    )

A.  B.  C.  D.

第II卷（非选择题）

二、填空题（本大题共7小题，共28.0分）

11.  若代数式有意义，则的取值范围是______ ．

12.  点关于轴的对称点是______．

13.  不等式组的解集是______．

14.  如图，把绕点顺时针旋转得到，此时于，已知，的度数是______

15.  若方程的一个根是，则代数式______．

16.  双曲线、在第一象限的图象如图，过上的任意一点，作轴的平行线交于，交轴于，若，则的值为______．

17.  如图，将等边的三条边向外延长一倍，得到第一个新的第二次将等边的三边向外延长一倍，得到第二个新的，依此规律继续延长下去，若的面积，则第个新的三角形的面积为______ ．

三、解答题（本大题共8小题，共62.0分。解答应写出文字说明，证明过程或演算步骤）

18.  本小题分
计算：．

19.  本小题分
先化简，再求值：，其中，．

20.  本小题分
如图，已知，，
请用直尺与圆规作图，作线段的垂直平分线，交于点，交于点不写作法，但要保留作图痕迹
若，若，则______．

21.  本小题分
春季开学后，某校为了让学生有效应用压岁钱，开展有意义的“尊老、敬老”慈善捐款活动，将捐款捐赠给本市敬老院学生会为了了解学生捐款的情况，随机调查了该校部分学生，根据调查结果，绘制了两幅不完整的统计图请根据相关信息，解答下列问题：

本次调查的学生人数为        人，在扇形统计图中，捐款金额为元所在扇形的圆心角的度数是        度，在调查的这组学生中，捐款金额的中位数是        元；
补全条形统计图；
学生会为了更好地引导学生合理支配压岁钱，选出甲，乙，丙和丁四人从不同的方面在全校进行讲解，但由于时间的限定，临时调整只能两人讲解因此，学生会采用随机抽签的方式从甲，乙，丙和丁四人中确定两名讲解人选请用列表或画树状图的方式说明抽中甲和乙的概率是多少？

22.  本小题分
如图，的半径为，经过上一点作的切线交半径的延长线于点，作的平分线交于点，交于点，延长交于点．
求证：；
如果，求的长度．

23.  本小题分
某学校计划从商店购买测温枪和洗手液，已知购买一个测温枪比购买一瓶洗手液多用元，若用元购买测温枪和用元购买洗手液，则购买测温枪的个数是购买洗手液个数的一半．
求购买一个测温枪、一瓶洗手液各需要多少元；
经商谈，商店给予该学校购买一个测温枪赠送一瓶洗手液的优惠，如果该学校需要洗手液个数是测温枪个数的倍还多个，且该学校购买测温枪和洗手液的总费用不超过元，那么该学校最多可购买多少个测温枪？

24.  本小题分
如图，在正方形中，点在边上不与点，重合，交对角线于点，交于点．
求证：．
若，，求的长．
如图，连接，，若，则 ______ ．

25.  本小题分
如图，抛物线与轴交于两点，，与轴交于点．
求抛物线的解析式；
过点作抛物线交于点，求四边形的面积；
在轴下方的抛物线上是否存在点，过作轴于点，使以、、为顶点的三角形与相似？若存在，则求出点的坐标；若不存在，请说明理由．

答案和解析

1.【答案】 

【解析】解：
A.是有理数，不是无理数，故本选项不符合题意；
B.是有理数，不是无理数，故本选项不符合题意；
C.是无理数，故本选项符合题意；
D.是有理数，不是无理数，故本选项不符合题意；
故选：．
根据无理数的定义逐个判断即可．
本题考查了无理数的定义，理解无理数的定义及其常见形式是解此题的关键，注意：无理数是指无限不循环小数．
 

2.【答案】 

【解析】解：，
故选：．
科学记数法的表示形式为的形式，其中，为整数．确定的值时，要看把原数变成时，小数点移动了多少位，的绝对值与小数点移动的位数相同．当原数绝对值时，是正整数；当原数的绝对值时，是负整数．
此题考查科学记数法的表示方法．科学记数法的表示形式为的形式，其中，为整数，表示时关键要正确确定的值以及的值．
 

3.【答案】 

【解析】解：、圆锥体的俯视图是圆，故此选项不合题意；
B、三棱柱的俯视图是三角形，故此选项符合题意；
C、球的俯视图是圆，故此选项不合题意；
D、圆柱体的俯视图是圆，故此选项不合题意；
故选：．
俯视图是从物体上面看所得到的图形，据此判断得出物体的俯视图．
本题考查了几何体的三视图，掌握定义是关键．注意所有的看到的棱都应表现在三视图中．
 

4.【答案】 

【解析】

【分析】
本题主要考查同底数幂的乘法、同底数幂的除法、幂的乘方以及积的乘方，熟练掌握同底数幂的乘法、同底数幂的除法、幂的乘方以及积的乘方是解决本题的关键．
根据同底数幂的乘法、同底数幂的除法、幂的乘方以及积的乘方解决此题．
【解答】
解：根据幂的乘方，得，故A符合题意．
B.根据同底数幂的乘法，得，故B不符合题意．
C.根据积的乘方，得，故C不符合题意．
D.根据同底数幂的除法，得，故D不符合题意．
故选：．  

5.【答案】 

【解析】利用多边形的外角和除以每个外角的度数，即可求得边数．
本题考查了多边形的外角和，理解任何多边形的外角和都是是解题关键．
解：这个多边形的边数是：．
故选：．
 

6.【答案】 

【解析】解：根据题意，
原抛物线顶点坐标为，平移后抛物线顶点坐标为，
平移后抛物线解析式为：．
故选：．
抛物线的平移问题，实质上是顶点的平移，原抛物线顶点坐标为，向左平移个单位，然后向下平移个单位后，顶点坐标为，根据抛物线的顶点式可求平移后抛物线的解析式．
本题考查了抛物线的平移与抛物线解析式的关系．关键是把抛物线的平移转化为顶点的平移，运用顶点式求抛物线的解析式．
 

7.【答案】 

【解析】解：，，
，
，
，
，
故选：．
根据两直线平行，内错角相等分别求出、，再根据平角的概念计算即可．
本题考查的是平行线的判定和性质，掌握平行线的性质是解题的关键．
 

8.【答案】 

【解析】解：由图象可得，一次函数图象在反比例函数图象上方时，自变量的取值范围为，
当时，自变量的取值范围为，
故选：．
根据函数图象得到两个交点的横坐标，再观察一次函数图象在反比例函数图象上方的部分，即可得到的取值范围．
本题考查反比例函数与一次函数的交点问题，解答本题的关键是明确题意，利用数形结合的思想解答．
 

9.【答案】 

【解析】首先根据圆周角定理可知，然后在中，根据锐角三角函数的定义求出的正弦值即可．
本题考查了圆周角定理，勾股定理，锐角三角函数的定义等知识，解答本题的关键是利用圆周角定理把求的正弦值转化成求的正弦值．
解：和所对的弧都是，
根据圆周角定理知．
在中，根据锐角三角函数的定义知，
，，
，
，
．
故选：．
 

10.【答案】 

【解析】解：如图，当点在处时，即当时，，
当点到达边高的位置时，
，此时最小，，
当时，点对应图末端时，即，
故A正确；
，
则，
故答案B正确；
，
，
，
故答案D正确；
，
故答案C不正确，
故选C．
分析当点在处，当点到达边高的位置时，点到达处时，对应个图中的位置关系去求解．
本题考查了动点问题的函数图象，了解图象中关键点所代表的实际意义，找到动点在两个图上的对应位置关系是解题关键．
 

11.【答案】 

【解析】解：代数式有意义，
，
解得：．
故的取值范围是．
故答案为：．
根据二次根式中的被开方数是非负数，进而得出答案．
此题主要考查了二次根式有意义的条件，正确掌握被开方数的符号是解题关键．
 

12.【答案】 

【解析】解：所求点与点关于轴对称，
所求点的横坐标为，纵坐标为，
点关于轴的对称点是．
故答案为．
让两点的横坐标互为相反数，纵坐标不变可得所求点的坐标．
考查两点关于轴对称的知识；用到的知识点为：两点关于轴对称，横坐标互为相反数，纵坐标相同．
 

13.【答案】 

【解析】解：，
由不等式，得，
由不等式，得，
故原不等式组的解集是，
故答案为：．
根据解一元一次不等式组的方法可以解答本题．
本题考查解一元一次不等式组，解答本题的关键是明确解一元一次不等式组的方法．
 

14.【答案】 

【解析】解：把绕点顺时针旋转得到，
，，
，
，
，
．
故答案为：．
由旋转的性质可得，，由直角三角形的性质可求．
本题考查了旋转的性质，熟练运用旋转的性质是本题的关键．
 

15.【答案】 

【解析】解：把代入，得
，
，
代数式．
故答案是：．
一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．
本题考查一元二次方程，解题的关键是正确理解一元二次方程的解的概念，本题属于基础题型．
 

16.【答案】 

【解析】解：由题意得：，
，
解得，，
故答案为：．
根据，列出方程，求出的值．
本题考查反比例函数系数的几何意义，过双曲线上的任意一点分别向两条坐标轴作垂线，与坐标轴围成的矩形面积就等于根据面积关系得出方程是解决问题的关键．
 

17.【答案】 

【解析】解：如图，连接，

，
，
，
用同样的方法得到，，，
；
向外扩展了一次得到的的面积为；
向外扩展了二次得到的，可以看作是向外扩展了一次得到，
的面积为的面积；
向外扩展了二次得到的的面积，，
同理：向外扩展了次得到的的面积为，
第个新的三角形的面积为，
故答案为：．
如图，连接，根据等底等高的三角形的面积相等求出的面积即可；根据等底等高的三角形的面积相等得到向外扩展了一次得到的的面积，向外扩展了二次得到的的面积，，找出规律即可．
本题考查规律型：图形变化类，首先应找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．探寻规律要认真观察、仔细思考，善用联想来解决这类问题．
 

18.【答案】解：


． 

【解析】先化简各式，然后再进行计算即可解答．
本题考查了实数的运算，负整数指数幂，特殊角的三角函数值，准确熟练地化简各式是解题的关键．
 

19.【答案】解：

，
当，时，原式． 

【解析】根据平方差公式和多项式除以单项式，可以将题目中的式子化简，然后将、的值代入化简后的式子计算即可．
本题考查整式的混合运算化简求值，解答本题的关键是明确整式混合运算的运算法则，注意平方差公式的应用．
 

20.【答案】 

【解析】解：如图，直线即为所求．


连接．
垂直平分线段，
，
，
，
，，
，
故答案为：．
作线段的垂直平分线交于点，交于点，直线即为所求．
证明，推出，可得，由此即可解决问题．
本题考查作图基本作图，线段的垂直平分线的性质，直角三角形的度角的性质等知识，解题的关键是理解题意，灵活运用所学知识解决问题．
 

21.【答案】     

【解析】解：捐款金额为元的有人，所占的百分比为，
这次被调查的学生共有：人；
捐款金额为元所在扇形的圆心角的度数是：；
捐款金额的中位数是第、两个数，即元；
故答案为：，，；
捐款金额为元对应人数为：人
捐款金额为元对应人数为：人；
补全条形统计图如图．

解：画树状图得：

共有种等可能的情况，恰好选中甲、乙两位同学的有种，
选中甲、乙．
由捐款金额为元的有人，所占的百分比为，即可求得这次被调查的学生数；用度乘以捐款金额为元所占的百分比，即可求得所占扇形的圆心角；根据中位数的求法可求得捐款金额的中位数；
首先求得捐款金额为元对应人数、捐款金额为元对应人数，即可补全统计图；
首先根据题意画出树状图，然后由树状图求得所有等可能的结果与恰好选中甲、乙两位同学的情况，再利用概率公式即可求得答案．
本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出，再从中选出符合事件或的结果数目，然后根据概率公式求出事件或的概率．也考查了条形统计图与扇形统计图的综合运用．
 

22.【答案】证明：，
，
平分，
，
，
；分

切于点，
，
，
，分
，
四边形是平行四边形，
，
平行四边形是菱形，分
，
是等边三角形，
，分
长度分 

【解析】由，平分，易证得，即可证得；
切于点，，易证得平行四边形是菱形，继而可证得是等边三角形，则可得：，继而求得的长度．
此题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式．此题难度适中，注意掌握数形结合思想的应用．
 

23.【答案】解：设购买一瓶洗手液需要元，则购买一个测温枪需要元，
依题意，得：，
解得：，
经检验，是原方程的解，且符合题意，
．
答：购买一个测温枪需要元，购买一瓶洗手液需要元．
设该学校购买个测温枪，则购买瓶洗手液，
依题意，得：，
解得：．
答：该学校最多可购买个测温枪． 

【解析】设购买一瓶洗手液需要元，则购买一个测温枪需要元，根据用元购买测温枪的数量是用元购买洗手液的一半，即可得出关于的分式方程，解之经检验后即可得出结论；
设该学校购买个测温枪，则购买瓶洗手液，根据总价单价数量结合总价不超过元，即可得出关于的一元一次不等式，解之取其中的最大值即可得出结论．
本题考查了分式方程的应用以及一元一次不等式的应用，解题的关键是：找准等量关系，正确列出分式方程；根据各数量之间的关系，正确列出一元一次不等式．
 

24.【答案】 

【解析】证明：连接，

四边形是正方形，
，，，
又，
≌，
，，
，且，
，
，
，
，
，
；
解：如图，过点作于，
，，
，
，
，，
，，
，
，
，负值舍去，
；
解：如图，在上截取，连接，

，，
，
，，
≌，
，，
，
，，
，，
，
，
，
，
，
．
故答案为：．
由“”可证≌，可得，，由四边形内角和定理可证，可得；
过点作于，利用勾股定理可求的长，即可求解；
在上截取，连接，由“”可证≌，可得，，可得，即可求解．
本题是四边形综合题，考查了正方形的性质，全等三角形的判定和性质，勾股定理，直角三角形的性质等知识，添加恰当辅助线是本题的关键．
 

25.【答案】解：依题意，得：，解得；
抛物线的解析式为：；
易知，，则直线的解析式为：；
由于，可设直线的解析式为，则有：，；
直线的解析式为；联立抛物线的解析式得：
，解得，；
；
；
，
是等腰直角三角形；
，
；
易求得，；
：：；
由于，若以、、为顶点的三角形与相似，则有：
∽或∽，得：
或；
即或；
设点的坐标为，
当时，，；
或
解得，舍去或，舍去；
点的坐标为：或；
当时，，；
或
解得，两个都不合题意，舍去或，舍去；
；
故存在符合条件的点，且坐标为：或或． 

【解析】此题主要考查了二次函数解析式的确定、图形面积的求法以及相似三角形的判定和性质等重要知识点，同时还考查了分类讨论的数学思想．
将、的坐标代入抛物线的解析式中，即可求出待定系数的值；
先求出直线的解析式，由于，那么直线的斜率与直线的相同，可据此求出直线的解析式，联立抛物线的解析式即可求出点的坐标；由图知四边形的面积是和的面积和，由此可求得其面积；
易知，那么是等腰直角三角形，由于，则；根据、的坐标可求出、的长，进而可求出它们的比例关系；若以、、为顶点的三角形与相似，那么两个直角三角形的对应直角边应该成立，可据此求出两条直角边的比例关系，连接抛物线的解析式即可求出点的坐标．