人教版数学九年年级上册 第23章 旋转测试卷（2）

这是一份人教版数学九年年级上册 第23章 旋转测试卷（2），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
第23章 旋转测试卷（2）
一、选择题
1．在平面直角坐标系中，已知点P的坐标是（﹣1，﹣2），则点P关于原点对称的点的坐标是（　　）
A．（﹣1，2） B．（1，﹣2） C．（1，2） D．（2，1）
2．△ABO与△A1B1O在平面直角坐标系中的位置如图所示，它们关于点O成中心对称，其中点A（4，2），则点A1的坐标是（　　）

A．（4，﹣2） B．（﹣4，﹣2） C．（﹣2，﹣3） D．（﹣2，﹣4）
3．在平面直角坐标系中，点P（﹣20，a）与点Q（b，13）关于原点对称，则a+b的值为（　　）
A．33 B．﹣33 C．﹣7 D．7
4．在直角坐标系中，将点（﹣2，3）关于原点的对称点向左平移2个单位长度得到的点的坐标是（　　）
A．（4，﹣3） B．（﹣4，3） C．（0，﹣3） D．（0，3）
5．在平面直角坐标系中，若点P（m，m﹣n）与点Q（﹣2，3）关于原点对称，则点M（m，n）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
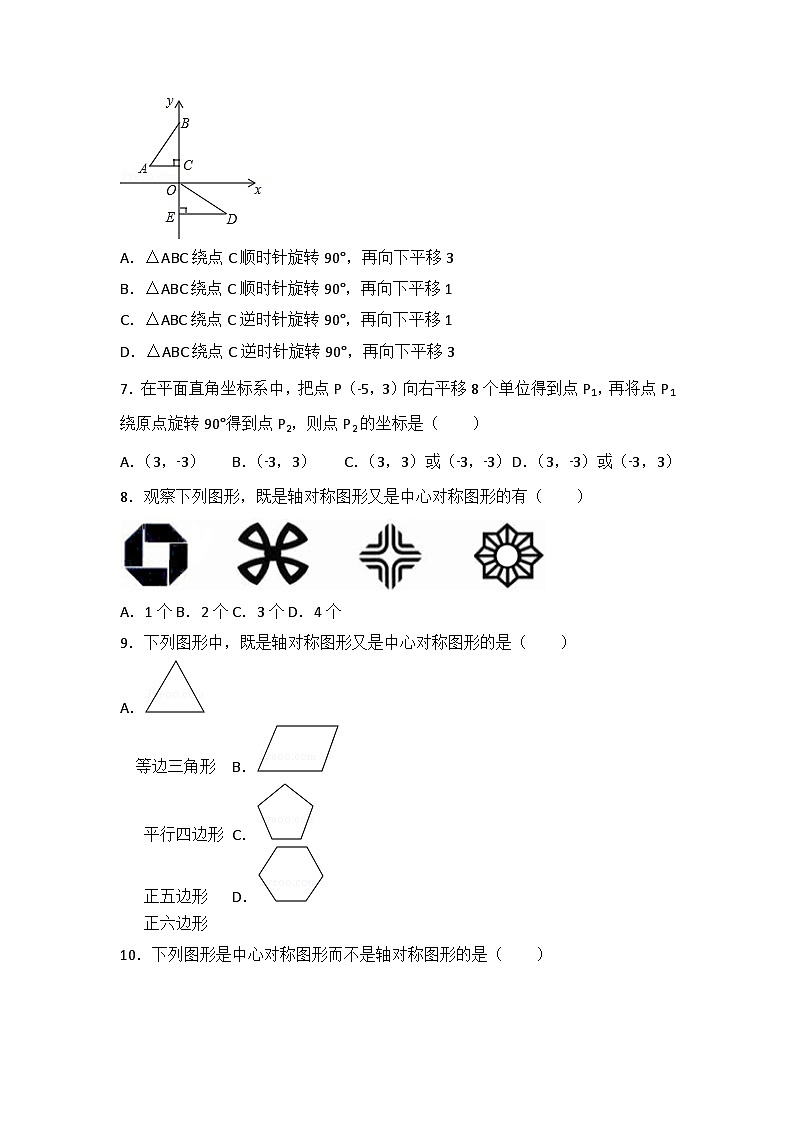
6．如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（　　）

A．△ABC绕点C顺时针旋转90°，再向下平移3
B．△ABC绕点C顺时针旋转90°，再向下平移1
C．△ABC绕点C逆时针旋转90°，再向下平移1
D．△ABC绕点C逆时针旋转90°，再向下平移3
7．在平面直角坐标系中，把点P（﹣5，3）向右平移8个单位得到点P1，再将点P1绕原点旋转90°得到点P2，则点P2的坐标是（　　）
A．（3，﹣3） B．（﹣3，3） C．（3，3）或（﹣3，﹣3） D．（3，﹣3）或（﹣3，3）
8．观察下列图形，既是轴对称图形又是中心对称图形的有（　　）

A．1个 B．2个 C．3个 D．4个
9．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A．
等边三角形 B．
平行四边形 C．
正五边形 D．
正六边形
10．下列图形是中心对称图形而不是轴对称图形的是（　　）
A． B． C． D．
11．下列图案中，不是中心对称图形的是（　　）
A． B． C． D．
12．在平面直角坐标系内，点P（﹣2，3）关于原点的对称点Q的坐标为（　　）
A．（2，﹣3） B．（2，3） C．（3，﹣2） D．（﹣2，﹣3）
13．将点P（﹣2，3）向右平移3个单位得到点P1，点P2与点P1关于原点对称，则P2的坐标是（　　）
A．（﹣5，﹣3） B．（1，﹣3） C．（﹣1，﹣3） D．（5，﹣3）
14．点A（3，﹣1）关于原点的对称点A′的坐标是（　　）
A．（﹣3，﹣1） B．（3，1） C．（﹣3，1） D．（﹣1，3）
15．在平面直角坐标系中，点A（﹣2，1）与点B关于原点对称，则点B的坐标为（　　）
A．（﹣2，1） B．（2，﹣1） C．（2，1） D．（﹣2，﹣1）
16．在直角坐标系中，点B的坐标为（3，1），则点B关于原点成中心对称的点的坐标为（　　）

A．（3，﹣1） B．（﹣3，1） C．（﹣1，﹣3） D．（﹣3，﹣1）
17．在平面直角坐标系中，P点关于原点的对称点为P1（﹣3，﹣），P点关于x轴的对称点为P2（a，b），则=（　　）
A．﹣2 B．2 C．4 D．﹣4
　
二、填空题
19．若点（a，1）与（﹣2，b）关于原点对称，则ab=　　．
20．在平面直角坐标系中，以原点为中心，把点A（4，5）逆时针旋转90°，得到的点A′的坐标为　　．
21．已知A点的坐标为（﹣1，3），将A点绕坐标原点顺时针90°，则点A的对应点的坐标为　　．
22．设点M（1，2）关于原点的对称点为M′，则M′的坐标为　　．
23．点P（5，﹣3）关于原点的对称点的坐标为　　．
24．在平面直角坐标系中，点（﹣3，2）关于原点对称的点的坐标是　　．
25．已知点P（3，2），则点P关于y轴的对称点P1的坐标是　　，点P关于原点O的对称点P2的坐标是　　．
26．在平面直角坐标系中，点P（5，﹣3）关于原点对称的点的坐标是　　．
27．如图是一圆锥，在它的三视图中，既是中心对称图形，又是轴对称图形的是它的　　视图（填“主”，“俯”或“左”）．

28．若将等腰直角三角形AOB按如图所示放置，OB=2，则点A关于原点对称的点的坐标为　　．

　
三、解答题
29．在平面直角坐标系xOy中，已知A（﹣1，5），B（4，2），C（﹣1，0）三点．
（1）点A关于原点O的对称点A′的坐标为　　，点B关于x轴的对称点B′的坐标为　　，点C关于y轴的对称点C的坐标为　　．
（2）求（1）中的△A′B′C′的面积．
30．如图，在平面直角坐标系中，A（﹣2，2），B（﹣3，﹣2）
（1）若点C与点A关于原点O对称，则点C的坐标为　　；
（2）将点A向右平移5个单位得到点D，则点D的坐标为　　；
（3）由点A，B，C，D组成的四边形ABCD内（不包括边界）任取一个横、纵坐标均为整数的点，求所取的点横、纵坐标之和恰好为零的概率．

　

参考答案与试题解析
一、选择题
1．在平面直角坐标系中，已知点P的坐标是（﹣1，﹣2），则点P关于原点对称的点的坐标是（　　）
A．（﹣1，2） B．（1，﹣2） C．（1，2） D．（2，1）
【考点】关于原点对称的点的坐标．
【专题】压轴题．
【分析】平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），据此即可求得点P关于原点的对称点的坐标．
【解答】解：∵点P关于x轴的对称点坐标为（﹣1，﹣2），
∴点P关于原点的对称点的坐标是（1，2）．
故选：C．
【点评】此题主要考查了关于原点对称点的坐标性质，这一类题目是需要识记的基础题，要熟悉关于原点对称点的横纵坐标变化规律．
　
2．△ABO与△A1B1O在平面直角坐标系中的位置如图所示，它们关于点O成中心对称，其中点A（4，2），则点A1的坐标是（　　）

A．（4，﹣2） B．（﹣4，﹣2） C．（﹣2，﹣3） D．（﹣2，﹣4）
【考点】关于原点对称的点的坐标．
【专题】几何图形问题．
【分析】根据两个点关于原点对称时，它们的坐标符号相反可得答案．
【解答】解：∵A和A1关于原点对称，A（4，2），
∴点A1的坐标是（﹣4，﹣2），
故选：B．
【点评】此题主要考查了关于原点对称的点的坐标，关键是掌握点的坐标的变化规律．
　
3．在平面直角坐标系中，点P（﹣20，a）与点Q（b，13）关于原点对称，则a+b的值为（　　）
A．33 B．﹣33 C．﹣7 D．7
【考点】关于原点对称的点的坐标．
【分析】先根据关于原点对称的点的坐标特点：横坐标与纵坐标都互为相反数，求出a与b的值，再代入计算即可．
【解答】解：∵点P（﹣20，a）与点Q（b，13）关于原点对称，
∴a=﹣13，b=20，
∴a+b=﹣13+20=7．
故选：D．
【点评】本题主要考查了关于原点对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于原点对称的点，横坐标与纵坐标都互为相反数．
　
4．在直角坐标系中，将点（﹣2，3）关于原点的对称点向左平移2个单位长度得到的点的坐标是（　　）
A．（4，﹣3） B．（﹣4，3） C．（0，﹣3） D．（0，3）
【考点】关于原点对称的点的坐标；坐标与图形变化-平移．
【分析】根据关于原点的点的横坐标互为相反数，纵坐标互为相反数，可得关于原点的对称点，根据点的坐标向左平移减，可得答案．
【解答】解：在直角坐标系中，将点（﹣2，3）关于原点的对称点是（2，﹣3），再向左平移2个单位长度得到的点的坐标是（0，﹣3），
故选：C．
【点评】本题考查了点的坐标，关于原点的点的横坐标互为相反数，纵坐标互为相反数；点的坐标向左平移减，向右平移加，向上平移加，向下平移减．
　
5．在平面直角坐标系中，若点P（m，m﹣n）与点Q（﹣2，3）关于原点对称，则点M（m，n）在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
【考点】关于原点对称的点的坐标．
【分析】根据平面内两点关于原点对称的点，横坐标与纵坐标都互为相反数，则m=2且n=﹣3，从而得出点M（m，n）所在的象限．
【解答】解：根据平面内两点关于原点对称的点，横坐标与纵坐标都互为相反数，
∴m=2且m﹣n=﹣3，
∴m=2，n=5
∴点M（m，n）在第一象限，
故选A．
【点评】本题考查了平面内两点关于原点对称的点，横坐标与纵坐标都互为相反数，该题比较简单．
　
6．如图，在平面直角坐标系中，点B、C、E、在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（　　）

A．△ABC绕点C顺时针旋转90°，再向下平移3
B．△ABC绕点C顺时针旋转90°，再向下平移1
C．△ABC绕点C逆时针旋转90°，再向下平移1
D．△ABC绕点C逆时针旋转90°，再向下平移3
【考点】坐标与图形变化-旋转；坐标与图形变化-平移．
【分析】观察图形可以看出，Rt△ABC通过变换得到Rt△ODE，应先旋转然后平移即可．
【解答】解：根据图形可以看出，△ABC绕点C顺时针旋转90°，再向下平移3个单位可以得到△ODE．
故选：A．
【点评】本题考查的是坐标与图形变化旋转和平移的知识，掌握旋转和平移的概念和性质是解题的关键．
　
7．在平面直角坐标系中，把点P（﹣5，3）向右平移8个单位得到点P1，再将点P1绕原点旋转90°得到点P2，则点P2的坐标是（　　）
A．（3，﹣3） B．（﹣3，3） C．（3，3）或（﹣3，﹣3） D．（3，﹣3）或（﹣3，3）
【考点】坐标与图形变化-旋转；坐标与图形变化-平移．
【专题】分类讨论．
【分析】首先利用平移的性质得出点P1的坐标，再利用旋转的性质得出符合题意的答案．
【解答】解：∵把点P（﹣5，3）向右平移8个单位得到点P1，
∴点P1的坐标为：（3，3），
如图所示：将点P1绕原点逆时针旋转90°得到点P2，则其坐标为：（﹣3，3），
将点P1绕原点顺时针旋转90°得到点P3，则其坐标为：（3，﹣3），
故符合题意的点的坐标为：（3，﹣3）或（﹣3，3）．
故选：D．

【点评】此题主要考查了坐标与图形的变化，正确利用图形分类讨论得出是解题关键．
　
8．观察下列图形，既是轴对称图形又是中心对称图形的有（　　）

A．1个 B．2个 C．3个 D．4个
【考点】中心对称图形；轴对称图形．
【分析】根据轴对称图形与中心对称图形的概念求解．
【解答】解：第一个图形不是轴对称图形，是中心对称图形，故本选项错误；
第二个图形既是轴对称图形又是中心对称图形；
第三个图形既是轴对称图形又是中心对称图形；
第四个图形既是轴对称图形又是中心对称图形；
所以，既是轴对称图形又是中心对称图形共有3个．
故选C．
【点评】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．
　
9．下列图形中，既是轴对称图形又是中心对称图形的是（　　）
A．等边三角形 B．平行四边形
C．正五边形 D．正六边形
【考点】中心对称图形；轴对称图形．
【分析】根据轴对称及中心对称概念，结合选项即可得出答案．
【解答】解：A、是轴对称图形，不是中心对称图形，故此选项错误；
B、是中心对称图形，不是轴对称图形，故此选项错误；
C、是轴对称图形，不是中心对称图形，故此选项错误；
D、是轴对称图形，也是中心对称图形，故此选项正确．
故选：D．
【点评】此题主要考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合，中心对称图形是要寻找对称中心，图形旋转180度后与原图形重合．
　
10．下列图形是中心对称图形而不是轴对称图形的是（　　）
A． B． C． D．
【考点】中心对称图形；轴对称图形．
【分析】根据轴对称图形与中心对称图形的概念求解．
【解答】解：A、是中心对称图形，不是轴对称图形；故A正确；
B、是中心对称图形，也是轴对称图形；故B错误；
C、是中心对称图形，也是轴对称图形；故C错误；
D、不是中心对称图形，是轴对称图形；故D错误；
故选A．
【点评】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．
　
11．下列图案中，不是中心对称图形的是（　　）
A． B． C． D．
【考点】中心对称图形．
【分析】根据中心对称图形的概念求解．
【解答】解：A、是中心对称图形，故A选项错误；
B、不是中心对称图形，故B选项正确；
C、是中心对称图形，故C选项错误；
D、是中心对称图形，故D选项错误；
故选：B．
【点评】本题考查了中心对称图形的知识，解题的关键是掌握中心对称图形的概念．中心对称图形是要寻找对称中心，旋转180°后重合．
　
12．在平面直角坐标系内，点P（﹣2，3）关于原点的对称点Q的坐标为（　　）
A．（2，﹣3） B．（2，3） C．（3，﹣2） D．（﹣2，﹣3）
【考点】关于原点对称的点的坐标．
【专题】常规题型．
【分析】平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y）．
【解答】解：根据中心对称的性质，得点P（﹣2，3）关于原点对称点P′的坐标是（2，﹣3）．
故选：A．
【点评】关于原点对称的点坐标的关系，是需要识记的基本问题．记忆方法是结合平面直角坐标系的图形记忆．
　
13．将点P（﹣2，3）向右平移3个单位得到点P1，点P2与点P1关于原点对称，则P2的坐标是（　　）
A．（﹣5，﹣3） B．（1，﹣3） C．（﹣1，﹣3） D．（5，﹣3）
【考点】关于原点对称的点的坐标；坐标与图形变化-平移．
【分析】首先利用平移变化规律得出P1（1，3），进而利用关于原点对称点的坐标性质得出P2的坐标．
【解答】解：∵点P（﹣2，3）向右平移3个单位得到点P1，
∴P1（1，3），
∵点P2与点P1关于原点对称，
∴P2的坐标是：（﹣1，﹣3）．
故选：C．
【点评】此题主要考查了关于原点对称点的性质以及点的平移规律，正确把握坐标变化性质是解题关键．
　
14．点A（3，﹣1）关于原点的对称点A′的坐标是（　　）
A．（﹣3，﹣1） B．（3，1） C．（﹣3，1） D．（﹣1，3）
【考点】关于原点对称的点的坐标．
【分析】直接根据关于原点对称的点的坐标特点即可得出结论．
【解答】解：∵两个点关于原点对称时，它们的坐标符号相反，
∴点A（3，﹣1）关于原点的对称点A′的坐标是（﹣3，1）．
故选C．
【点评】本题考查的是关于原点对称的点的坐标，熟知关于原点对称的点的坐标特点是解答此题的关键．
　
15．在平面直角坐标系中，点A（﹣2，1）与点B关于原点对称，则点B的坐标为（　　）
A．（﹣2，1） B．（2，﹣1） C．（2，1） D．（﹣2，﹣1）
【考点】关于原点对称的点的坐标．
【分析】关于原点的对称点，横纵坐标都变成原来相反数，据此求出点B的坐标．
【解答】解：∵点A坐标为（﹣2，1），
∴点B的坐标为（2，﹣1）．
故选B．
【点评】本题考查了关于原点对称的点的坐标特点：两个点关于原点对称时，它们的坐标符号相反，即点P（x，y）关于原点O的对称点是P′（﹣x，﹣y）．
　
16．在直角坐标系中，点B的坐标为（3，1），则点B关于原点成中心对称的点的坐标为（　　）

A．（3，﹣1） B．（﹣3，1） C．（﹣1，﹣3） D．（﹣3，﹣1）
【考点】关于原点对称的点的坐标．
【分析】平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y）．
【解答】解：点（3，1）关于原点中心对称的点的坐标是（﹣3，﹣1），
故选D．
【点评】此题主要考查了关于原点对称的点坐标的关系，是需要识记的基本问题，记忆方法是结合平面直角坐标系的图形记忆．
　　
17．在平面直角坐标系中，P点关于原点的对称点为P1（﹣3，﹣），P点关于x轴的对称点为P2（a，b），则=（　　）
A．﹣2 B．2 C．4 D．﹣4
【考点】关于原点对称的点的坐标；立方根；关于x轴、y轴对称的点的坐标．
【专题】计算题．
【分析】利用关于原点对称点的坐标性质得出P点坐标，进而利用关于x轴对称点的坐标性质得出P2坐标，进而得出答案．
【解答】解：∵P点关于原点的对称点为P1（﹣3，﹣），
∴P（3，），
∵P点关于x轴的对称点为P2（a，b），
∴P2（3，﹣），
∴==﹣2．
故选：A．
【点评】此题主要考查了关于原点对称点的性质以及关于x轴对称点的性质，得出P点坐标是解题关键．
　
二、填空题
19．若点（a，1）与（﹣2，b）关于原点对称，则ab=　　．
【考点】关于原点对称的点的坐标．
【分析】平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），即：求关于原点的对称点，横纵坐标都变成相反数．记忆方法是结合平面直角坐标系的图形记忆．
【解答】解：∵点（a，1）与（﹣2，b）关于原点对称，
∴b=﹣1，a=2，
∴ab=2﹣1=．
故答案为：．
【点评】此题考查了关于原点对称的点的坐标，这一类题目是需要识记的基础题，记忆时要结合平面直角坐标系．
　
20．在平面直角坐标系中，以原点为中心，把点A（4，5）逆时针旋转90°，得到的点A′的坐标为　（﹣5，4）　．
【考点】坐标与图形变化-旋转．
【分析】首先根据点A的坐标求出OA的长度，然后根据旋转变换只改变图形的位置，不改变图形的形状与大小，可得OA′=OA，据此求出点A′的坐标即可．
【解答】解：如图，过点A作AC⊥y轴于点C，作AB⊥x轴于点B，过A′作A′E⊥y轴于点E，作A′D⊥x轴于点D，，
∵点A（4，5），
∴AC=4，AB=5，
∵点A（4，5）绕原点逆时针旋转90°得到点A′，
∴A′E=AB=5，A′D=AC=4，
∴点A′的坐标是（﹣5，4）．
故答案为：（﹣5，4）．
【点评】此题主要考查了坐标与图形变换﹣旋转，要熟练掌握，解答此题的关键是要明确：旋转变换只改变图形的位置，不改变图形的形状与大小．
　
21．已知A点的坐标为（﹣1，3），将A点绕坐标原点顺时针90°，则点A的对应点的坐标为　（3，1）　．
【考点】坐标与图形变化-旋转．
【分析】过A作AC⊥y轴于C，过A'作A'D⊥y轴于D，根据旋转求出∠A=∠A'OD，证△AC0≌△ODA'，推出A'D=OC=1，OD=CA=3，即可根据题意作出A点绕坐标原点顺时针90°后的点，然后写出坐标．
【解答】解：过A作AC⊥y轴于C，过A'作A'D⊥y轴于D，
∵∠AOA'=90°，∠ACO=90°，
∴∠AOC+∠A'OD=90°，∠A+∠AOC=90°，
∴∠A=∠A'OD，
在△AC0和△ODA'中，
，
∴△AC0≌△ODA'（AAS），
∴A'D=OC=1，OD=CA=3，
∴A'的坐标是（3，1）．
故答案为：（3，1）．

【点评】本题主要考查对坐标与图形变换﹣旋转，全等三角形的性质和判定等知识点的理解和掌握，能正确画出图形并求出△AC0≌△ODA'是解此题的关键．
　
22．设点M（1，2）关于原点的对称点为M′，则M′的坐标为　（﹣1，﹣2）　．
【考点】关于原点对称的点的坐标．
【分析】根据关于原点对称的点的坐标特点：两个点关于原点对称时，它们的坐标符号相反可直接得到答案．
【解答】解：点M（1，2）关于原点的对称点M′的坐标为（﹣1，﹣2），
故答案为：（﹣1，﹣2）．
【点评】此题主要考查了关于原点对称的点的坐标特点，关键是熟练掌握点的坐标的变化规律．
　
23．点P（5，﹣3）关于原点的对称点的坐标为　（﹣5，3）　．
【考点】关于原点对称的点的坐标．
【分析】两点关于原点对称，横坐标互为相反数，纵坐标互为相反数．
【解答】解：∵5的相反数是﹣5，﹣3的相反数是3，
∴点P（5，﹣3）关于原点的对称点的坐标为 （﹣5，3），
故答案为：（﹣5，3）．
【点评】主要考查两点关于原点对称的坐标的特点：两点关于原点对称，两点的横坐标互为相反数，纵坐标互为相反数，用到的知识点为：a的相反数为﹣a．
　
24．在平面直角坐标系中，点（﹣3，2）关于原点对称的点的坐标是　（3，﹣2）　．
【考点】关于原点对称的点的坐标．
【专题】数形结合．
【分析】根据平面直角坐标系内两点关于原点对称横纵坐标互为相反数，即可得出答案．
【解答】解：根据平面直角坐标系内两点关于原点对称横纵坐标互为相反数，
∴点（﹣3，2）关于原点对称的点的坐标是（3，﹣2），
故答案为（3，﹣2）．
【点评】本题主要考查了平面直角坐标系内两点关于原点对称横纵坐标互为相反数，难度较小．
　
25．已知点P（3，2），则点P关于y轴的对称点P1的坐标是　（﹣3，2）　，点P关于原点O的对称点P2的坐标是　（﹣3，﹣2）　．
【考点】关于原点对称的点的坐标；关于x轴、y轴对称的点的坐标．
【分析】根据关于y轴对称的点的横坐标互为相反数，纵坐标相同；
关于原点对称的点的横坐标与纵坐标都互为相反数解答．
【解答】解：点P（3，2）关于y轴的对称点P1的坐标是（﹣3，2），
点P关于原点O的对称点P2的坐标是（﹣3，﹣2）．
故答案为：（﹣3，2）；（﹣3，﹣2）．
【点评】本题考查了关于原点对称点点的坐标，关于y轴对称的点的坐标，熟记对称点的坐标特征是解题的关键．
　
26．在平面直角坐标系中，点P（5，﹣3）关于原点对称的点的坐标是　（﹣5，3）　．
【考点】关于原点对称的点的坐标．
【分析】根据关于坐标原点对称的点的横坐标与纵坐标都互为相反数解答．
【解答】解：点P（5，﹣3）关于原点对称的点的坐标是（﹣5，3）．
故答案为：（﹣5，3）．
【点评】本题考查了关于原点对称的点的坐标，熟记关于坐标原点对称的点的横坐标与纵坐标都互为相反数是解题的关键．
　
27．如图是一圆锥，在它的三视图中，既是中心对称图形，又是轴对称图形的是它的　俯　视图（填“主”，“俯”或“左”）．

【考点】中心对称图形；轴对称图形；简单几何体的三视图．
【分析】先判断圆锥的三视图，然后结合中心对称及轴对称的定义进行判断即可．
【解答】解：圆锥的主视图是等腰三角形，是轴对称图形，但不是中心对称图形；
圆锥的左视图是等腰三角形，是轴对称图形，但不是中心对称图形；
圆锥的俯视图是圆，是轴对称图形，也是中心对称图形；
故答案为：俯．
【点评】本题考查了简单几何体的三视图、轴对称及中心对称的定义，解答本题关键是判断出圆锥的三视图．
　
28．若将等腰直角三角形AOB按如图所示放置，OB=2，则点A关于原点对称的点的坐标为　（﹣1，﹣1）　．

【考点】关于原点对称的点的坐标．
【分析】过点A作AD⊥OB于点D，根据等腰直角三角形的性质求出OD及AD的长，故可得出A点坐标，再由关于原点对称的点的坐标特点即可得出结论．
【解答】解：过点A作AD⊥OB于点D，
∵△AOB是等腰直角三角形，OB=2，
∴OD=AD=1，
∴A（1，1），
∴点A关于原点对称的点的坐标为（﹣1，﹣1）．
故答案为（﹣1，﹣1）．

【点评】本题考查的是关于原点对称的点的坐标特点，熟知等腰直角三角形的性质是解答此题的关键．
　
三、解答题
29．在平面直角坐标系xOy中，已知A（﹣1，5），B（4，2），C（﹣1，0）三点．
（1）点A关于原点O的对称点A′的坐标为　（1，﹣5）　，点B关于x轴的对称点B′的坐标为　（4，﹣2）　，点C关于y轴的对称点C的坐标为　（1，0）　．
（2）求（1）中的△A′B′C′的面积．
【考点】关于原点对称的点的坐标；三角形的面积；关于x轴、y轴对称的点的坐标．
【分析】（1）关于原点对称的两点的横、纵坐标都是互为相反数；关于x轴对称的两点的横坐标相同，纵坐标互为相反数；关于y轴对称的两点的横坐标互为相反数，纵坐标相同；
（2）根据点A′（1，﹣5），B′（4，﹣2），C′（1，0）在平面直角坐标系中的位置，可以求得A′C′=5，B′D=3，所以由三角形的面积公式进行解答．
【解答】解：（1）∵A（﹣1，5），
∴点A关于原点O的对称点A′的坐标为（1，﹣5）．
∵B（4，2），
∴点B关于x轴的对称点B′的坐标为（4，﹣2）．
∵C（﹣1，0），
∴点C关于y轴的对称点C′的坐标为（1，0）．
故答案为：（1，﹣5），（4，﹣2），（1，0）．

（2）如图，∵A′（1，﹣5），B′（4，﹣2），C′（1，0）．
∴A′C′=|﹣5﹣0|=5，B′D=|4﹣1|=3，
∴S△A′B′C′=A′C′•B′D=×5×3=7.5，即（1）中的△A′B′C′的面积是7.5．

【点评】本题考查了关于原点、x轴、y轴对称的点的坐标，三角形的面积．解答（2）题时，充分体现了“数形结合”数学思想的优势．
　
30．如图，在平面直角坐标系中，A（﹣2，2），B（﹣3，﹣2）
（1）若点C与点A关于原点O对称，则点C的坐标为　（2，﹣2）　；
（2）将点A向右平移5个单位得到点D，则点D的坐标为　（3，2）　；
（3）由点A，B，C，D组成的四边形ABCD内（不包括边界）任取一个横、纵坐标均为整数的点，求所取的点横、纵坐标之和恰好为零的概率．

【考点】关于原点对称的点的坐标；坐标与图形变化-平移；概率公式．
【分析】（1）根据关于原点的对称点，横纵坐标都互为相反数求解即可；
（2）把点A的横坐标加5，纵坐标不变即可得到对应点D的坐标；
（3）先找出在平行四边形内的所有整数点，再根据概率公式求解即可．
【解答】解：（1）∵点C与点A（﹣2，2）关于原点O对称，
∴点C的坐标为（2，﹣2）；
（2）∵将点A向右平移5个单位得到点D，
点D的坐标为（3，2）；
（3）由图可知：A（﹣2，2），B（﹣3，﹣2），C（2，﹣2），D（3，2），
∵在平行四边形ABCD内横、纵坐标均为整数的点有15个，其中横、纵坐标和为零的点有3个，即（﹣1，1），（0，0），（1，﹣1），
∴P==．

【点评】本题考查了关于原点对称的点的坐标，坐标与图形变化﹣平移，概率公式．难度适中，掌握规律是解题的关键．