2023年河北省保定市莲池区中考二模数学试卷（含答案）

2023年初中毕业生升学文化课模拟考试

数学试卷

注意事项：1.本试卷共8页，总分120分，考试时间120分钟.

2.答题前，考生务必将姓名、准考证号填写在答题卡上相应的位置.

3.所有答案均在答题卡上作答，在本试卷或草稿纸上作答无效.答题前，请仔细阅读答题卡上的“注意事项”，按照“注意事项”的规定答题.

4.答选择题时，用2B铅笔将答题卡上对应题目的答题标号涂黑；答非选择题时，请在答题卡上对应题目的答题区域内答题.

一、选择题（本大题共16个小题.1-10小题每题3分，11-16小题每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1.计算得，则“？”是（    ）

A.0 B.1 C.2 D.3

2.围棋起源于中国，古代称之为“弈”，至今已有四千多年的历史.下列由黑、白棋子摆成的图案中.是轴对称图形的是（    ）

A.  B.  C.  D.

3.按照有理数加法法则，计算的正确过程是（    ）

A. B. C. D.

4.如图，将折叠，使点落在边处，展开后得到折痕，则是的（    ）

A.高线 B.角平分线 C.中线 D.中位线

5.下列选项是无理数的是（    ）

A. B. C. D.

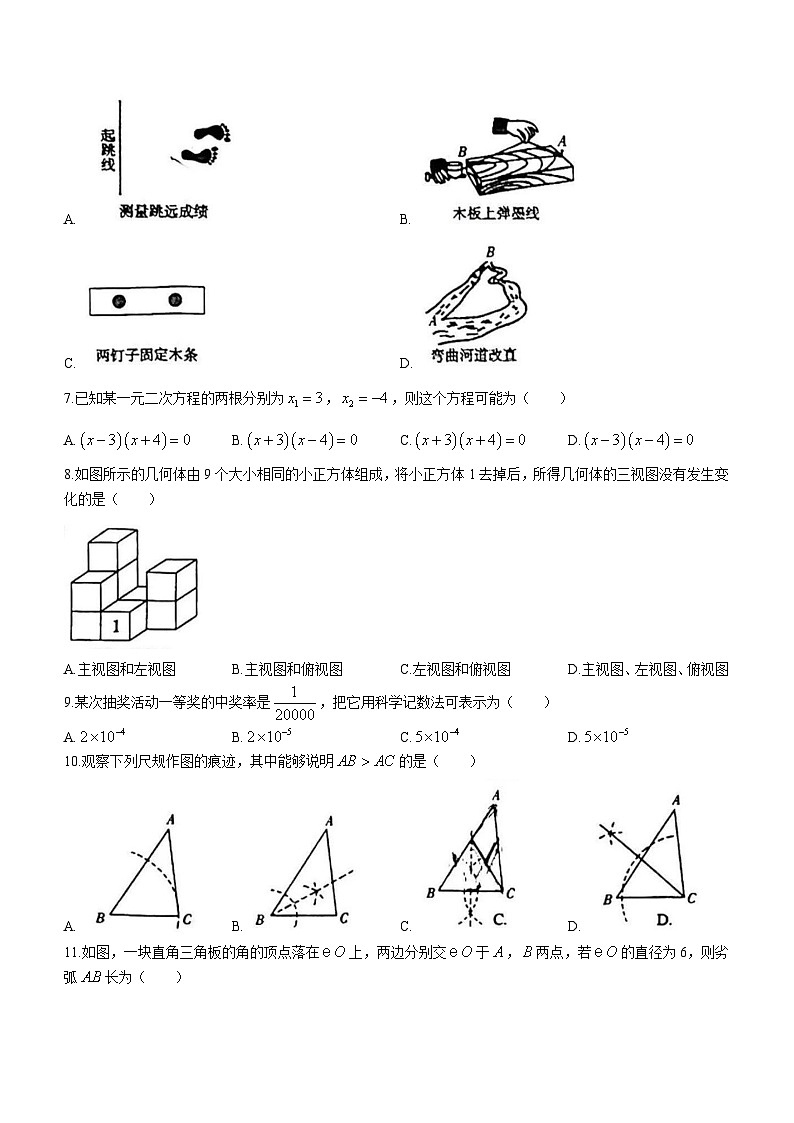
6.下列各选项中能用“垂线段最短”来解释的现象是（    ）

A.  B.  

C.   D.

7.已知某一元二次方程的两根分别为，，则这个方程可能为（    ）

A. B. C. D.

8.如图所示的几何体由9个大小相同的小正方体组成，将小正方体1去掉后，所得几何体的三视图没有发生变化的是（    ）

A.主视图和左视图 B.主视图和俯视图 C.左视图和俯视图 D.主视图、左视图、俯视图

9.某次抽奖活动一等奖的中奖率是，把它用科学记数法可表示为（    ）

A. B. C. D.

10.观察下列尺规作图的痕迹，其中能够说明的是（    ）

A.  B.  C.  D.

11.如图，一块直角三角板的角的顶点落在上，两边分别交于，两点，若的直径为6，则劣弧长为（    ）

A.3 B. C. D.6

12.“二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界誉为“中国第五大发明”.嘉嘉购买了“二十四节气”主题邮票，他要将“雨水”“惊蛰”“春分”“清明”“谷雨”五张邮票中的两张送给好朋友淇淇.嘉嘉将它们背面朝上放在桌面上（邮票背面完全相同），让淇淇从中随机抽取一张（不放回），再从剩下的邮票中随机抽取一张，则淇淇抽到的两张邮票恰好是“惊蛰”和“谷雨”的概率是（    ）

A. B. C. D.

13.如图所示，正五边形的顶点，在射线上，顶点在射线上，，则的度数为（    ）

A.72° B.80° C.50° D60°

14.已知点，在二次函数的图象上，若，则的取值范围为（    ）

A. B. C. D.

15.如图，在平行四边形中，按下列条件得到的四边形不一定是平行四边形的是（    ）

A.，是过对角线交点的两条线段 B.，，，是四边形各边中点 

C.，  D.，，，是角平分线

16.已知某函数的图象经过，两点，几名同学给出了如下四个推断：

甲：若该函数的图象为直线，则此函数的图象与直线平行；

乙：若该函数的图象为双曲线，则也在此函数图象上；

丙：若该函数的图象为抛物线，且开口向下，则此函数图象一定与轴的负半轴相交；

丁：若该函数的图象为抛物线，且开口向上，则此函数图象的对称轴在直线的左侧；

推断合理的是（    ）

A.甲、乙 B.乙、丙 C.丙、丁 D.乙、丁

二、填空题（本大题共3个小题.17、18小题每题3分，19小题第一空1分，第二空2分，共9分）

17.计算：_____________.

18.以下是淇淇妈妈做晚饭时食材准备及加工时间列表，有一个炒菜锅，一个电饭煲，一个煲汤锅，两个燃气灶可用，做好这顿晚餐一般情况下至少需要_________分钟.

19.小颖在一次拼图游戏中，发现了一个有趣的现象：她先用图形①②③④⑤拼出了矩形；接着拿走图形⑤.通过平移的方法，用①②③④拼出了矩形.已知，图形④的面积为9，请你帮助她解决下列问题：

（1）拿走的图形⑤的面积为：____________.

（2）当，时，则____________.

三、解答题（本大题共7个小题，共69分.解答题应写出文字说明、证明过程或演算步骤）

20.（9分）下图是学习分式方程应用时，老师板书的问题和两名同学所列的方程.

根据以上信息，解答下列问题：

（1）甲同学所列方程中的表示____________；乙同学所列方程中的表示_____________________；

（2）两个方程中任选一个，解方程并回答老师提出的问题.

21.（9分）张老师为了了解她所教1班、2班本学期课外名著阅读情况，分别从两班随机抽取20名同学进行调查，并把调查结果制成如图所示不完整的扇形统计图和条形统计图.

（1）1班课外名著阅读情况扇形统计图中“7本”所在扇形的圆心角是_________；请补充2班课外名著阅读情况中“9本”的条形统计图；

（2）已知2班阅读数量的平均数为6本，方差为7.6，请你计算1班的平均数和方差，并判断哪个班阅读情况比较稳定；

（3）从2班所选样本中选取名同学的阅读数量.并与1班样本组成一组新数据，发现新数据的中位数小于原1班样本的中位数.若取最小值时，求这名同学的阅读量和的最大值.

22.（9分）嘉嘉在某次作业中得到如下结果：

，

，

，

，

.

据此，嘉嘉猜想：对于任意锐角，，若，均有.

（1）当，时，验证是否成立？

（2）嘉嘉的猜想是否成立？若成立，请结合如图所示给予证明，其中所对的边为，所对的边为，斜边为；若不成立，请举出一个反例；

（3）利用上面的证明方法，直接写出与，之间的关系.

23.（10分）如图，直线经过，两点.已知点，点是线段上一动点（可与点，重合），直线（为常数）经过点，交于点.

（1）求直线的函数表达式；

（2）当时，求点的坐标；

（3）直线必过点____________，在点移动的过程中，的取值范围为__________.

24.（10分）已知线段长为8，点为线段的中点，将线段绕点逆时针旋转60°，得到扇形和扇形.如图（1）所示固定扇形不动，将扇形绕点逆时针旋转，如图（2），连接，，设旋转角.

（1）求证：；

（2）当点落在边上时，与扇形所在的圆存在怎样的位置关系？说明理由；

（3）当，，三点共线时，线段的长是___________.

25.（10分）嘉琪家里有一款高脚杯，她发现高脚杯的杯体可以近似看成抛物线.于是她开始进行测量，并画出了高脚杯的截面图（杯体厚度忽略不计）如图（1）.点是抛物线的顶点，.点是的中点，且，，杯子的高度（即，之间的距离）为20cm.嘉琪想借此考查一下对学过的知识掌握情况，于是以为原点，所在直线为轴，所在直线为轴，建立平面直角坐标系（1个单位长度表示1cm），并提出了以下问题，你也来一起解决吧！

（1）求杯体所在抛物线的解析式；

（2）将杯子向左平移3cm，并倒满饮料，杯体与轴交于点，如图（2），过点放一根吸管，吸管底部碰触到杯壁后不再移动，喝过一次饮料后发现剩余饮料的液面低于点，设吸管所在直线的解析式为，求的取值范围；

（3）将放在水平桌面上的装有饮料的高脚杯绕点顺时针旋转30°，液面恰好到达点处（），如图（3）.

①请你以的中点为原点，所在直线为轴，所在直线为轴，建立平面直角坐标系，并求出与轴的交点坐标；

②请直接写出此时杯子内液体的最大深度.

26.（12分）如图，已知正方形的边长为8个单位长，点为边上的中点，点从点向点以1个单位长/秒速度匀速运动，连接，过点做的垂线，交于点.交射线于点.设点运动时间为.

（1）用含的代数式表示长为___________；

（2）如图，点在边上，且，求点在内部（包括边上）的时长；

（3）①求证：点一定在的外接圆上；

②当的外接圆与相切时，求的值；

（4）线段长的最小值是____________.

2023莲池区初三模拟考试数学答案

一、选择题（本大题共16个小题.1~10小题每题3分，11~16小题每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的）

二、填空题：（本大题共3个小题.17、18小题每题3分，19小题第一空1分，第二空2分，共9分）

17. 18.33 19.3、49

三、解答题（本大题共7个小题.共69分.解答题应写出文字说明、证明过程或演算步骤）

20.（1）江水的流速

轮船以最大航速沿江顺流航行110km所用时间（或轮船以最大航速逆流航行90km所用时间）

（2）选甲：

两边都乘以得解得

经检验是原方程的根

答：江水流速为5km/h.

选乙：

两边都乘以得解得

经检验是原方程的根

答：江水流速为5km/h.

21.（1）72，9本所对应的数字为4

解：（2）1班平均数为（本）

方差为（）

∵，∴1班阅读情况更稳定.

（3）把1班数据按从小到大顺序排列4、4、5、5、5、5、6、6、6、6、6、6、6、6、7、7、7、7、8、8，发现中位数为6本，加入2班名同学后中位数变小，要使这名同学的阅读量的和最大，且最小，则应加入4个5和4个4，此时新数据中位数为本.所以为8，这名同学阅读量的和为本.

22.解：（1）∵，∴

（2）成立.证明：在中，且

∴.

（3）.

23.解：（1）设直线的函数表达式为

将，代入得解得

∴直线的函数表达式为.

（2）当时，直线的函数表达式为

∴解得∴

（3） 且或.

24.（1）证明：由题意得

∴，即

在和中

∴∴

（2）相切.理由如下：

如图，连接

∵，，∴为等边三角形

∴，

又∵为中点∴，∴

∴，∴∴

又∵为扇形所在圆的半径，∴与扇形所在圆相切.

（3）或

提示：过点作的垂线，利用三角函数和勾股定理.

25.解：（1）设抛物线表达式为

∵，∴，又∵杯子高20cm，∴

将，代入解得.

∴杯体所在抛物线表达式为

（2）杯子平移后顶点坐标为，设平移后表达式为

当时，

∴，点关于对称轴对称的点

由平移可知

当直线经过点时解得，∴

当直线经过点时解得

∴，∴.

（3）①建立如图1所示平面直角坐标系，设与轴交于点，与轴交于点，与轴交于点.

∵，，∴

∵，∴

∵，，∴，∴

∴与轴交点坐标为.

最大深度为cm.

提示：如图2，过杯体最低点作直线，交轴于点，此时直线与抛物线有且只有一个交点.

设直线的解析式为，由（1）可知抛物线解析式为

令，，，∴

∴直线的解析式为，

作直线于点

∵，∴，∴

∴最大深度为cm.

26.解：（1）

提示：∵四边形为正方形，且边长为8

∴，，

又∵为中点，∴，∴

∵，∴，∴

∴，∴，，∴

（2）当过点时（或当点与点重合时）

∴，，，

∴点在内部的时长为.

（3）①如图1，连接，取中点，连接、

∵，，∴

∴点在的外接圆上.

②由①可知点为外接圆圆心，作于点

∵为外接圆半径，该圆与相切∴

∴四边形为矩形，∴

∵，∴，∴，∴

在中

∴.

（4）最小值为.

提示：方法一：如图2，在点从向运动的过程中，点由无限远处向点运动.当外接圆与相切时，最小.由（3）可知，∴，∴.

方法二：如图3，作延长线于点，易证，

∴，，∴，∴

∴可以看成是函数和图象上当相同时两点之间的距离.

通过平移直线，发现当直线与只有一个交点时，直线与直线的垂直距离为最小值.

，，

，∵，∴

此时两直线间的距离即为和之间的最小距离，为.