数学（云南卷）2023年中考考前最后一卷（参考答案）

2023年中考考前最后一卷【云南卷】

数学·参考答案

第Ⅰ卷

一、选择题（本大题共12个小题，每小题3分，共36分，每小题均有四个选项，其中只有一项符合题目要求）

二、填空题（本大题共6个小题，每小题3分，共18分）

13．【答案】a≥－2且

14．【答案】

15．【答案】

16．【答案】5

17．【答案】150°

18．【答案】45°

三、解答题（本大题共6个小题，共46分）

19．(本题5分)

【答案】（1）；（2）；作图见解析；（3）；（4）

【详解】解（1）设调查学生总人数为

则有

解得

故答案为．

（2）羽毛球部分的学生占总人数的，

羽毛球的人数为

故答案为．

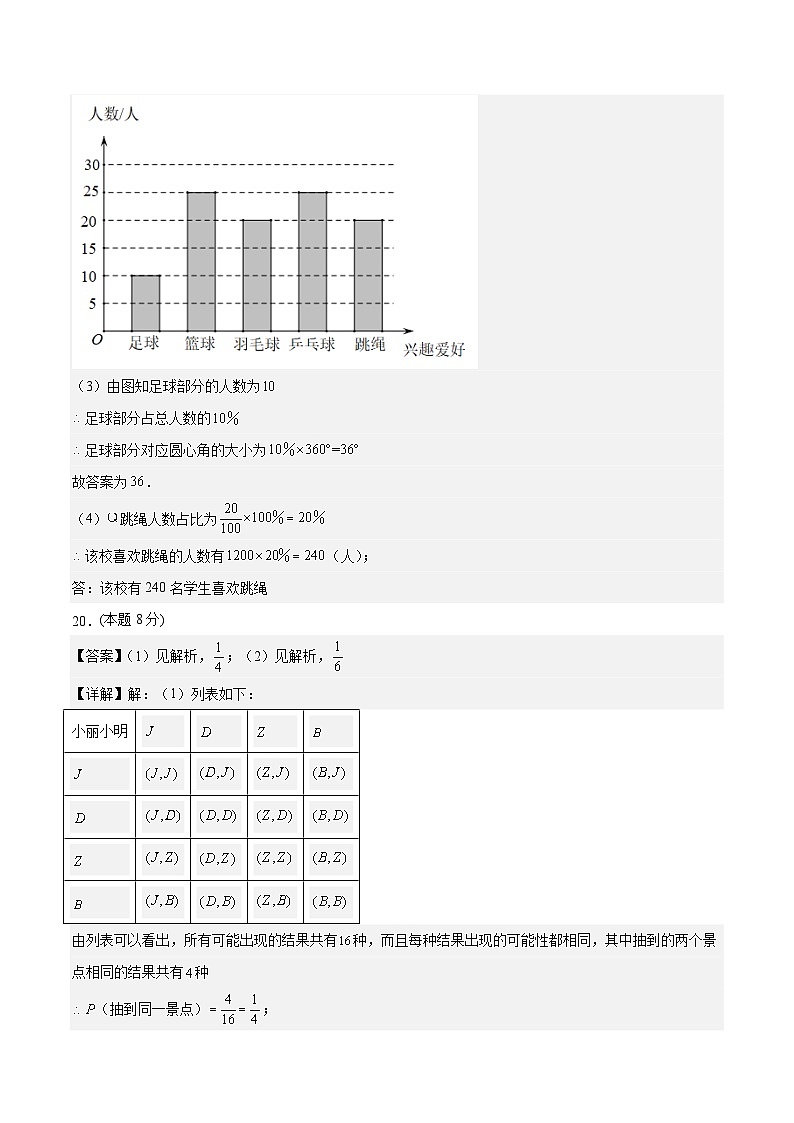
统计图补充如图所示：

（3）由图知足球部分的人数为

足球部分占总人数的

足球部分对应圆心角的大小为

故答案为．

（4）跳绳人数占比为

该校喜欢跳绳的人数有（人）；

答：该校有240名学生喜欢跳绳

20．(本题8分)

【答案】（1）见解析，；（2）见解析，

【详解】解：（1）列表如下：

由列表可以看出，所有可能出现的结果共有种，而且每种结果出现的可能性都相同，其中抽到的两个景点相同的结果共有种

（抽到同一景点）；

（2）画树状图如下：

由树状图可以看出，所有可能出现的结果共有种，而且每种结果出现的可能性都相同，其中两人抽到太原动物园和太原植物园共有种

（抽到太远动物园和太原植物园）．

21．(本题8分)

【答案】(1)见解析

(2)见解析

【详解】（1）解：证明：平分，

，

，

，

，

，

，

；

（2）如图，过作，

平分，，，

，，

，

，，

，

在和中，

，

，

．

即．

22．(本题8分)

【答案】(1)计划调配36座新能源客车6辆，该大学共有218名志愿者

(2)租车方案为：需租用36座客车3辆，22座客车5辆．

【解析】(1)

解：设计划调配36座新能源客车x辆，该大学共有y名志愿者，

由题意得：，

解得，

∴计划调配36座新能源客车6辆，该大学共有218名志愿者，

答：计划调配36座新能源客车6辆，该大学共有218名志愿者；

(2)

解：设需租用36座客车m辆，22座客车 辆，租车费用为W，

由题意得： ，

∵，

∴，

∵，

∴W随m增大而增大，

∴当m=3时，W最小，

∴租车方案为：需租用36座客车3辆，22座客车5辆．

23．(本题8分)

【答案】（1）详见解析；（2）OA =；（3）p为定值16.

【详解】（1）证明：

∵四边形ABCD为正方形

∴∠D=∠C=90°，

∴∠DOM=90°-∠OMD，

∵MN为切线，

∴OM⊥MN，

∴∠NMC=90°-∠OMD =∠DOM，

∴Rt△DOM∽Rt△CMN.

（2）设OA=y，Rt△ODM中，DM 2=OM 2- DO 2= OA 2- DO2,

即x2=y2-(8-y)2,解得OA=y=

（3）在Rt△ODM中，

设△ODM的周长P′=

由（1）知△DOM ∽△CMN，相似比为，

故p=.

故p为定值16.

【点睛】本题考查切线性质，相似三角形的判定和性质，正方形的性质，勾股定理.难度较大.

24．(本题9分)

【答案】(1)

(2)m1=3或m2=-1

(3)点Q的坐标为（3，2）或（-1，0）时，以点B，Q，M为顶点的三角形与△BOD相似．

【详解】（1）

把A（-1，0），B（4，0）代入y=ax2+bx+2，

得，

解得，

∴该抛物线的函数表达式为．

（2）

设直线BD的函数表达式为y=kx+b，

抛物线，当x=0时，y=2，

∴C（0，2），

∵点D与点C（0，2）关于x轴对称，

∴D（0，-2），

将B（4，0），D（0，-2）代入y=kx+b，

得，

解得：，

∴直线BD的函数表达式为，

∵QM⊥x轴于点P，交抛物线于点Q，交BD所在直线于点M．且P（m，0），

∴Q（m，-m2+m+2），M（m，m-2），

则QM=（-m2+m+2）-（m-2）=-m2+m+4，

∵F（0，），D（0，-2），

∴DF=-（-2）=，

∵QM∥DF，

∴当QM=DF时，四边形DMQF是平行四边形，

∴-m2+m+4=，

解得m1=3或m2=-1，如图1、图2，

∴m1=3或m2=-1时，四边形DMQF是平行四边形．

（3）

∵QM∥DF，

∴∠QMB=∠ODB，

①如图3，当∠MBQ=∠DOB=90°时，△MBQ∽△DOB，

则，

∴，

∵∠MBQ=90°，

∴∠MBP+∠PBQ=90°，

∵∠MPB=∠BPQ=90°，

∴∠MBP+∠BMQ=90°，

∴∠BMQ=∠PBQ，

∵∠MBQ=∠BPQ=90°，

∴△MBQ∽△BPQ，

∴，

∴，

∴，

解得m1=3，m2=4（不符合题意，舍去），

∴Q（3，2）；

②如图4，当∠BQM=90°时，此时点Q与点A重合，△BQM∽△BOD，

此时m=-1，点Q的坐标为（-1，0），

综上，点Q的坐标为（3，2）或（-1，0）时，以点B，Q，M为顶点的三角形与△BOD相似．