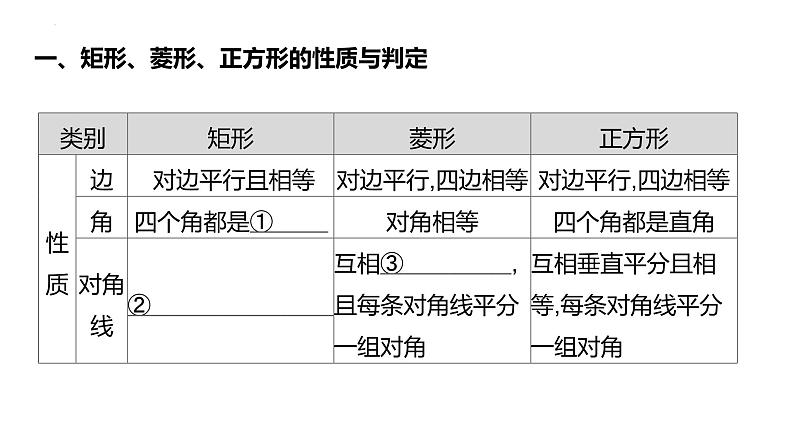
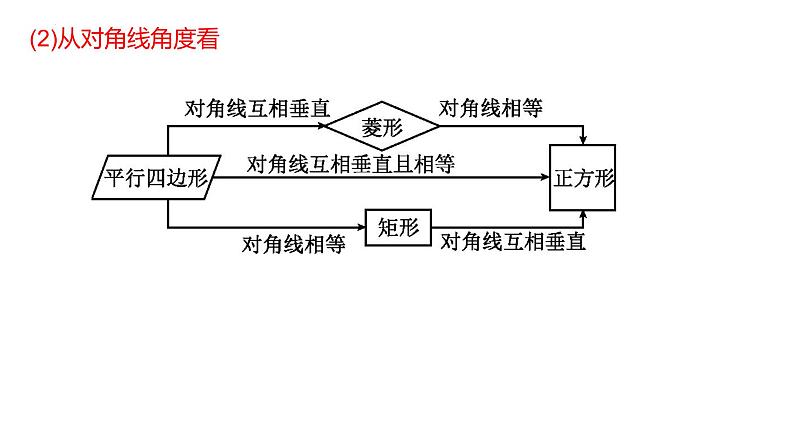
2023年九年级中考数学一轮复习 矩形课件PPT

这是一份2023年九年级中考数学一轮复习 矩形课件PPT，共19页。PPT课件主要包含了2从对角线角度看等内容，欢迎下载使用。

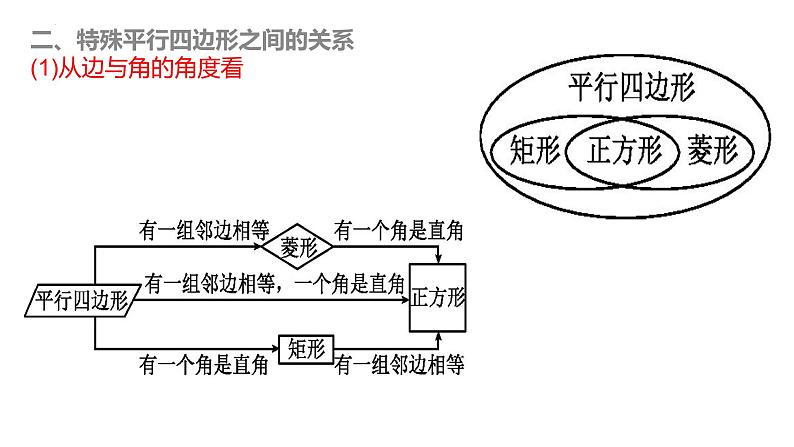
二、特殊平行四边形之间的关系(1)从边与角的角度看
1．（2022•陕西）在下列条件中，能够判定▱ABCD为矩形的是（　　）A．AB＝AD B．AC⊥BD C．AB＝AC D．AC＝BD
2．（2022•无锡）雪花、风车……展示着中心对称的美，利用中心对称，可以探索并证明图形的性质．请思考在下列图形中，是中心对称图形但不一定是轴对称图形的为（　　）A．扇形 B．平行四边形 C．等边三角形 D．矩形
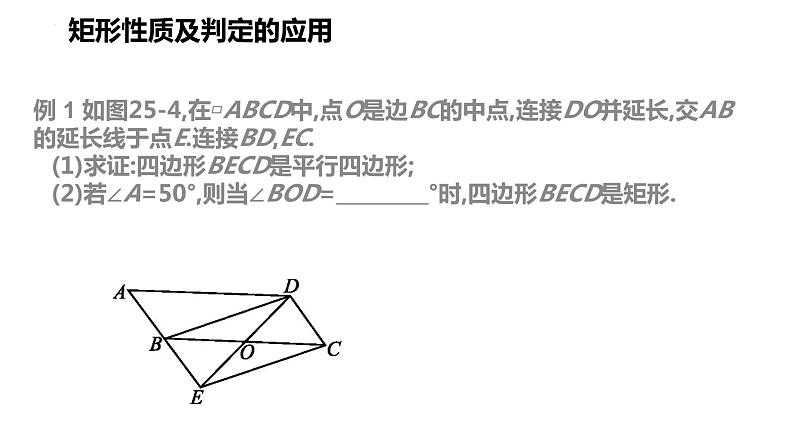
例 1 如图25-4,在▱ABCD中,点O是边BC的中点,连接DO并延长,交AB的延长线于点E.连接BD,EC.(1)求证:四边形BECD是平行四边形;(2)若∠A=50°,则当∠BOD=　　　　°时,四边形BECD是矩形. 
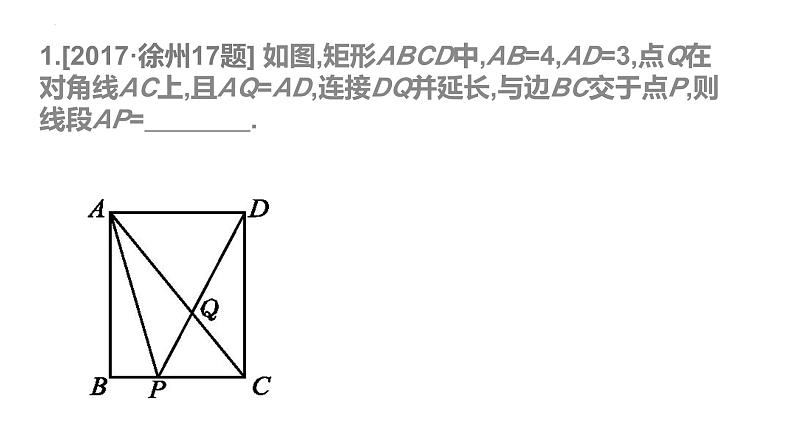
1.[2017·徐州17题] 如图,矩形ABCD中,AB=4,AD=3,点Q在对角线AC上,且AQ=AD,连接DQ并延长,与边BC交于点P,则线段AP=　　　　. 
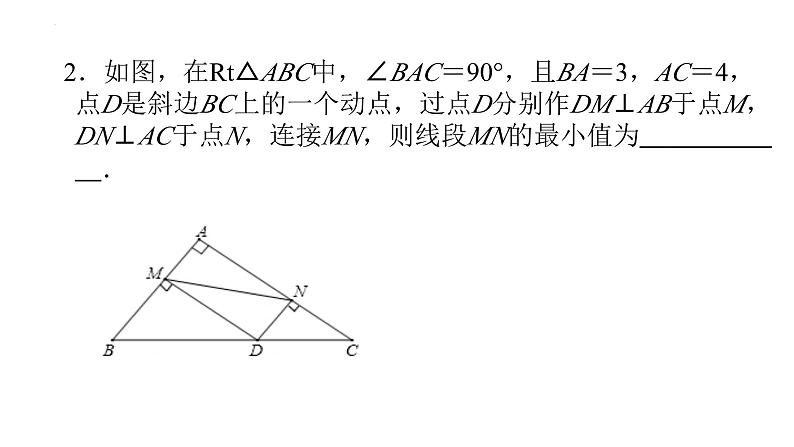
2．如图，在Rt△ABC中，∠BAC＝90°，且BA＝3，AC＝4，点D是斜边BC上的一个动点，过点D分别作DM⊥AB于点M，DN⊥AC于点N，连接MN，则线段MN的最小值为　 　．
3.如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE=　　　.
4.如图,四边形ABCD与四边形AEGF均为矩形,点E,F分别在线段AB,AD上.若BE=FD=2 cm,矩形AEGF的周长为20 cm,则图中阴影部分的面积为　　　　 cm2. 
例2．（2022•苏州）如图，将矩形ABCD沿对角线AC折叠，点B的对应点为点E，AE与CD交于点F．（1）求证：△DAF≌△ECF；（2）若∠FCE＝40°，求∠CAB的度数．
1.[2021·徐州22题]如图,将一张长方形纸片ABCD沿EF折叠,使C,A两点重合,点D落在点G处.已知AB=4,BC=8.(1)求证:△AEF是等腰三角形;(2)求线段FD的长.
2．（2022•丽水）如图，将矩形纸片ABCD折叠，使点B与点D重合，点A落在点P处，折痕为EF．（1）求证：△PDE≌△CDF；（2）若CD＝4cm，EF＝5cm，求BC的长．
4．（2022•青海）如图，矩形ABCD的对角线相交于点O，过点O的直线交AD，BC于点E，F，若AB＝3，BC＝4，则图中阴影部分的面积为 　 　．
3（2022•黔东南州）如图，矩形ABCD的对角线AC，BD相交于点O，DE∥AC，CE∥BD．若AC＝10，则四边形OCED的周长是 　 　．
例3．（2022•泰州）如图，线段DE与AF分别为△ABC的中位线与中线．（1）求证：AF与DE互相平分；（2）当线段AF与BC满足怎样的数量关系时，四边形ADFE为矩形？请说明理由．
1.（2022•十堰）如图，▱ABCD中，AC，BD相交于点O，E，F分别是OA，OC的中点．（1）求证：BE＝DF；
（2）设 ，当k为何值时，四边形DEBF是矩形？请说明理由．
2.（2022•恩施州）如图，在四边形ABCD中，∠A＝∠B＝90°，AD＝10cm，BC＝8cm，点P从点D出发，以1cm/s的速度向点A运动，点M从点B同时出发，以相同的速度向点C运动，当其中一个动点到达端点时，两个动点同时停止运动．设点P的运动时间为t（单位：s），下列结论正确的是（　　）
A．当t＝4s时，四边形ABMP为矩形B．当t＝5s时，四边形CDPM为平行四边形C．当CD＝PM时，t＝4sD．当CD＝PM时，t＝4s或6s
例4（2022•盐城）如图，在矩形ABCD中，AB＝2BC＝2，将线段AB绕点A按逆时针方向旋转，使得点B落在边CD上的点B'处，线段AB扫过的面积为 　 　．