




必刷卷03——2023年中考数学考前30天冲刺必刷卷(浙江宁波专用)
展开绝密★启用前
2023年中考数学考前信息必刷卷03
数 学(浙江宁波专用)
2023年宁波中考数学结构和分值没有变化,满分150分,题型仍然是10(选择题)+6(填空题)+8(解答题),但考查内容要关注基础性、综合性、应用型和创新性,要关注学科主干知识,对学科基本概念、基本原理和思想方法的考查;从考查内容上看,随着数学教学的逐步深入,为体现数学课程标准对数学教学
课改的要求,课程内容的学习,不会单纯考查学生死记硬背的机械记忆力,重视学生的数学活动,发展学生的情感、符号感、空间观念、统计观念以及推理能力。从知识点的分布看,实数的有关概念及其运算,代数式的化简求值,探究规律,方程不等式组的解法及函数知识的综合应用,直线型的相关性质,仍将是考试的重点。对于函数侧重考查一次函数、反比例函数的性质以及函数的应用、函数与方程不等式之间的联系,二次函数的综合问题常以解答的形式出现;对三角形的全等、相似的证明,特殊四边形的判定及性质的应用,也将以解答题的形式出现。此外,统计与概率也是必考内容。对圆的知识考查,尤其是切线的判定,强化数学意识的转化和应用能力。
通过对考试信息的梳理以及教学研究成果,中考试卷侧重增加文化的考查,加强问题背景的设置,加大考查的深度和广度..同时应加强学生的画图能力、识图能力、动手能力、探究能力、思维能力,注重数学思维方法的训练.对于创新型试题要增加思维的含量,重点考查学生将新知识转化为旧知识的能力。在教学中应引导学生弄清算理来提高运算能力. 对于选择题1-5题考查的是科学记数法、幂的运算及整式的运算,二次根式有意义的条件,倒数,加权平均数;第6题是一元一次不等式的应用。第7题是三视图,第8题是一次函数的图象与坐标轴的面积。第9题是圆中阴影部分面积的计算,第10题是四边形综合问题;对于填空题第11-13题考查的是因式分解、实数的性质、概率公式,第14题考查的是反比例函数的图象,第15题考查的是圆的切线的存在性问题,第16题考查的是正方形与旋转的最值问题;对于解答题,第17题考查分式的加减、二元一次方程组的解,第18题考察的是基本作图与命题,第19题
考查解直角三角形的应用,第20题考查读频数分布直方图的能力和利用统计图获取信息的能力,第21题考查待定系数法求二次函数、以及二次函数的性质,第22题考查了反比例函数的实际应用,第23题
考查了正方形的性质,全等三角形的判定的性质,相似三角形的判定和性质;第24题是圆的综合问题,
考查了圆周角定理,圆的有关性质,等腰三角形的性质,等边三角形的判定与性质,平行线分线段成比例定理,相似三角形的判定与性质.
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.习近平总书记提出精准扶贫战略以来,各地积极推进精准扶贫,加大帮扶力度,全国脱贫人口数不断增加,脱贫人口接近1100万人,将数据1100万用科学记数法表示为( )
A.0.11×108 B.1.1×107 C.1.1×108 D.11×106
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>10时,n是正数;当原数的绝对值<1时,n是负数.
【详解】解:1100万=1100 0000=1.1×107,
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.下列运算正确的是( )
A.a2+a2=a4 B.a3﹣a2=a C.a3•a2=a6 D.a6÷a3=a3
【分析】根据同底数幂乘法、除法法则,合并同类项法则求解即可.
【详解】解:A. a2+a2=2a2,故A不符合题意;
B. a3﹣a2=a2(a﹣1),故B不符合题意;
C. a3•a2=a5,故C不符合题意;
D. a6÷a3=a3.故D符合题意.
故选:D.
【点睛】此题考查了同底数幂乘法、除法法则,合并同类项法则,熟记这些法则是解题的关键.
3.若代数式有意义,则实数x的取值范围是( )
A.x≠1 B.x≥0 C.x>0 D.x≥0且x≠1
【分析】根据二次根式有意义的条件列出不等式,解不等式即可.
【详解】解:由题意得,x≥0,
故选:B.
【点睛】本题考查的是二次根式有意义的条件,掌握二次根式中的被开方数必须是非负数是解题的关键.
4.与互为倒数的是( )
A. B.3×4 C. D.﹣3×4
【分析】先根据有理数减法的法则计算=﹣,再求倒数即可.
【详解】解:=,
∴与互为倒数的是﹣12.
故选:D.
【点睛】本题考查了倒数以及有理数的减法和乘法运算法则,熟记概念和相关运算法则是解题的关键,倒数:乘积是1的两数互为倒数.
5.某博物馆拟招聘一名优秀志愿讲解员,其中某位志愿者笔试、试讲、面试三轮测试得分分别为90分、94分、92分,综合成绩中笔试占30%,试讲占50%,面试占20%,则该名志愿者的综合成绩为( )
A.92分 B.92.4分 C.90分 D.94分
【分析】根据加权平均数的定义列式计算即可.
【详解】解:该名志愿者的综合成绩为90×30%+94×50%+92×20%=92.4(分),
故选:B.
【点睛】本题主要考查加权平均数,解题的关键是掌握加权平均数的定义.
6.某次知识竞赛共20道题,每一题答对得10分,不答得0分,答错扣5分.小聪有一道题没答,竞赛成绩超过90分.设他答对了x道题,则根据题意可列出不等式为( )
A.10x﹣5(19﹣x)≥90 B.10x﹣5(19﹣x)>90
C.10x﹣(19﹣x)≥90 D.10x﹣(19﹣x)>90
【分析】小聪答对题的得分:10x;小聪答错的得分:﹣5(19﹣x),不等关系:小聪得分超过90分.
【详解】解:设他答对了x道题,根据题意,得
10x﹣5(19﹣x)>90.
故选:B.
【点睛】此题主要考查了由实际问题抽象出一元一次不等式,抓住关键词语,找到不等关系是解题的关键.
7.把7个同样大小的正方体形状的积木堆放在桌子上,从前、后、左、右四个方向看,所看到的都是如图所示的同样的图形,则其从上面看到的形状图不可能是( )
A. B.
C. D.
【分析】由从前、后、左、右四个方向看可得俯视图有三行三列,依此找到不符合的从上面看到的形状图即可求解.
【详解】解:由从前、后、左、右四个方向看,所看到的都是如图:所示的同样的图形,
可知从上面看到的形状图有三行三列,且左视图最左边有两个罗列.
只有选项C不符合题意.
故选:C.
【点睛】此题考查了从不同的方向观察物体和几何体,锻炼了学生的空间想象力和抽象思维能力.
8.在同一个平面直角坐标系中一次函数y=x+b图象与反比例函数y=的图象相交于A、B两点,若原点为O点,连接过OA、OB、AB.若△AOB面积为4,则b的值为( )
A.﹣1或2 B.1或﹣2 C.±1 D.±2
【分析】设点A的坐标为(x1,y1),B(x2,y2).x1和x2是方程x2+bx﹣3=0的两个解.由韦达定理可得x1+x2=﹣b,x1•x2=﹣3,|x1﹣x2|==.由一次函数得出点C的坐标,利用三角形的面积公式可求出b的值.
【详解】解:设点A的坐标为(x1,y1),B(x2,y2).
令x+b=,得x2+bx﹣3=0,
则x1和x2是方程x2+bx﹣3=0的两个解,
∴x1+x2=﹣b,x1•x2=﹣3,
∴|x1﹣x2|==.
∵y=x+b与y轴交于点C,
∴C(0,b),
∴OC=|b|.
∵△AOB面积为4,
∴|b|•|x1﹣x2|=4,即|b|•=4,
解得b2=4或b2=﹣16(舍去),
∴b=±2.
故选:D.
【点睛】本题是反比例函数与一次函数的交点问题,考查了待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,数形结合是解题的关键.
9.如图,在扇形AOB中,∠AOB=90°,点C在上,且的长为π,点D在OA上,连接BD,CD,若点C,O关于直线BD对称,则图中阴影部分的面积为( )
A. B. C. D.
【分析】连接BC,OC,OC交BD于W,根据对称求出BC=OB,求出△COB是等边三角形,求出∠COB=60°,根据弧长公式求出OB=3,求出∠AOC=30°,求出DW,再求出答案即可.
【详解】解:连接BC,OC,OC交BD于W,
∵点C,O关于直线BD对称,
∴∠DWO=90°,OW=CW,BC=OB,
∵OC=OB,
∴OC=BC=OB,
即△OCB是等边三角形,
∴∠COB=60°,
∵的长为π,
∴=π,
解得:OB=3,
即OC=OB=3,
∴OW=CW=1.5,
∵∠AOB=90°,
∴∠AOC=30°,
∴OD=2DW,
由勾股定理得:OD2=DW2+OW2,
即(2DW)2=DW2+1.52,
解得:DW=(负数舍去),
∴阴影部分的面积S=S扇形AOC﹣S△DOC=﹣=,
故选:A.
【点睛】本题考查了轴对称的性质,扇形面积的计算,弧长公式的计算,等边三角形的性质和判定,直角三角形的性质等知识点,能综合运用知识点进行计算是解此题的关键.
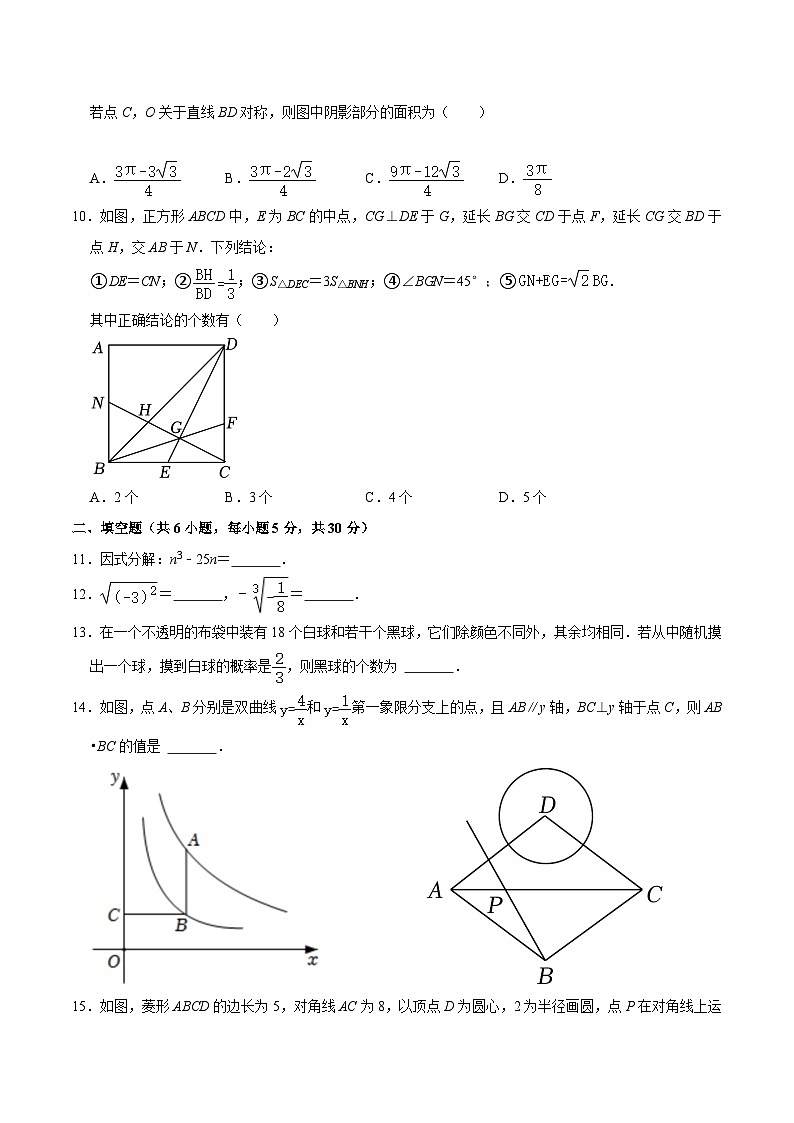
10.如图,正方形ABCD中,E为BC的中点,CG⊥DE于G,延长BG交CD于点F,延长CG交BD于点H,交AB于N.下列结论:
①DE=CN;
②;
③S△DEC=3S△BNH;
④∠BGN=45°;
⑤.
其中正确结论的个数有( )
A.2个 B.3个 C.4个 D.5个
【分析】①根据题目已知△NBC≌△ECD,可以判断①正确;
②证明△NBH∽△CDH可以判断②正确;
③过点H作AD的平行线,根据线段比例关系,得出面积比可以判断③正确;
④过点B作两条垂线,利用三角形全等可以判断④正确;
⑤连接NE,结合勾股定理和相似可以求出BG、BF的长,判断⑤正确.
【详解】解:①在正方形ABCD中,∠NBC=∠ECD=90°,
∴BC=CD,∠BCN+∠GCD=90°,
∵CG⊥DE,
∴∠CDG+∠GCD=90°,
∴∠BCN=∠CDG,
∴△NBC≌△ECD(ASA),
∴DE=CN,
故①正确;
②在正方形ABCD中,AB∥CD,
∴△NBH∽△CDH,
∴,
∵△NBC≌△ECD(ASA),E为BC的中点,四边形ABCD是正方形,
∴NB=BC=CD,
∴=,
∴=,
故②正确;
③如下图所示,过H点作IJ∥AD,
∵△NBH∽△CDH,
∴IJ=HJ,
∴HI=IJ=DC,
∴S△DEC=EC•DC,S△BNH=BN•HI=EC×DC=×(×EC•DC),
∴S△DEC=3 S△BNH,
故③正确;
④过点B作BP⊥CN于点P,BQ⊥DG交DE的延长线上于点Q,
∴∠BPC=∠BQD=∠PGQ=90°,
∴四边形PBQG是矩形,
∴∠PBQ=90°,
∵∠ABC=90°,
∴∠NBP=∠QBE,
由①得△NBC≌△ECD,
∴EC=BN,
∵E是BC的中点,
∴BE=EC,
∴BE=BN,
∵∠BPN=∠BQE=90°,
∴△BPN≌△BQE(AAS),
∴BP=BQ,
∴四边形PBQG是正方形,
∴∠BGE=45°,
故④正确;
⑤如图所示,连接NE,
设BN=x,则BE=EC=x,BC=2x,
∵CG⊥DE,∠NBC=90°,
∴CN===x,
EN===x,
由△ECN面积可得CN•GE=EC•BN,
∴GE=x,
∴GN==x,
∴GN+GE=x+x=x,
∴GC=CN﹣GN=xx=x,
∵AB∥CD,
∴△NGB∽△CGF,
∴=,
∴BG=FG,
∴BG=BF,FC=BN=x,
∴BG=×x=x,
∴GN+GE=BG,
故⑤正确;
故选:D.
【点睛】本题是四边形综合题,考查了正方形的性质,三角形全等的判定与性质、相似三角形的判定与性质等知识点,学生要有较强的综合知识,解决复杂问题的能力.
二、填空题(共6小题,每小题5分,共30分)
11.因式分解:n3﹣25n= n(n+5)(n﹣5) .
【分析】先提取公因式n,再根据平方差公式进行二次分解即可求得答案.
【详解】解:n3﹣25n=n(n2﹣52)=n(n+5)(n﹣5).
故答案为:n(n+5)(n﹣5).
【点睛】本题考查了提公因式法和公式法因式分解.注意提取公因式后利用平方差公式进行二次分解,注意分解要彻底.
12.= 3 ,﹣= .
【分析】依据算术平方根、立方根的定义求解即可.
【详解】解:==3.
﹣=﹣(﹣)=.
故答案为:3;.
【点睛】本题主要考查的是算术平方根和立方根的定义,熟练掌握算术平方根、立方根的定义是解题的关键.
13.在一个不透明的布袋中装有18个白球和若干个黑球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,摸到白球的概率是,则黑球的个数为 9 .
【分析】设黑球的个数为x个,根据概率公式列出方程,求出x的值即可得出答案.
【详解】解:设黑球的个数为x个,根据题意得:
=,
解得:x=9,
经检验x=9是方程的解,
答:黑球的个数为9;
故答案为9.
【点睛】此题主要考查了概率公式的应用,一般方法为:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.
14.如图,点A、B分别是双曲线和第一象限分支上的点,且AB∥y轴,BC⊥y轴于点C,则AB•BC的值是 3 .
【分析】延长AB交x轴于点D,过点A作AE⊥y轴于点E,利用k的几何意义,求得矩形ADOE的面积为4,矩形BDOC的面积为1,即可求得矩形ABCE的面积为3,据此求解即可.
【详解】解:延长AB交x轴于点D,过点A作AE⊥y轴于点E,
∵AB∥y轴,BC⊥y轴,
∴四边形ADOE、ABCE、BDOC都是矩形,
∵点A、B分别是双曲线和第一象限分支上的点,
∴矩形ADOE的面积为4,矩形BDOC的面积为1,
∴矩形ABCE的面积为4﹣1=3,
∴AB•BC=3,
故答案为:3.
【点睛】本题考查了反比例函数的系数k的几何意义.根据面积关系得出AB•BC的值是解决问题的关键.
15.如图,菱形ABCD的边长为5,对角线AC为8,以顶点D为圆心,2为半径画圆,点P在对角线上运动,当射线BP与圆D相切时,AP的长是 4﹣或4+ .
【分析】连接BD交AC于点H,当射线BP与⊙D相切于点E时,连接DE,分两种情况,当射线BP与⊙D相切于点E,当射线BP与⊙D相切于点F时,然后利用菱形的性质,以及相似三角形的判定与性质进行计算即可解答.
【详解】解:连接BD交AC于点H,当射线BP与⊙D相切于点E时,连接DE,如图:
∵四边形ABCD是菱形,
∴AB=BC=5,AC⊥BD,AH=AC=4,BD=2BH,
在Rt△ABH中,BH===3,
∴BD=2BH=6,
∵射线BP与⊙D相切于点E,
∴∠DEB=90°,
∴BE===4,
∵∠DEB=∠BHP=90°,∠PBH=∠DBE,
∴△BHP∽△BED,
∴=,
∴=,
∴PH=,
∴AP=AH﹣PH=4﹣,
当射线BP与⊙D相切于点F时,如图:
同理可得:PH=,
∴AP=AH+PH=4+,
综上所述,当射线BP与圆D相切时,AP的长是4﹣或4+,
故答案为:4﹣或4+.
【点睛】本题考查了菱形的性质,相似三角形的判定与性质,勾股定理,分两种情况进行计算即可解答.
16.如图,正方形ABCD的边长为4,正方形CEFG的边长为,将正方形CEFG绕点C旋转,BG和DE相交于点K,则AK的最大值是 4 ,连结BE,当点C正好是△BKE的内心时,CK的长是 .
【分析】证明∠DKB=90°,从而确定点K在以BD为直径的圆上运动;根据内心特征,确定内心点C到BE的距离,进一步得出结果.
【详解】解:如图,
连接AC,BD,CF和EG,AC,BD交于点O,DC,BG交于点M,作CQ⊥BE于Q,作CR⊥BK于R,
∵四边形ABCD和四边形EFGC是正方形,
∴BC=CD,CG=CE,∠BCD=∠ECG=90°,∠ECF=45°,AC=,EN=CN=,
∴∠BCD+∠DCG=∠ECG+∠DCG,
∴∠BCG=∠DCE,
∴△BCG≌△DCE(SAS),
∴∠BGC=∠CDE,
∵∠BMC=∠DMK,
∴∠BKD=∠BCD=90°,
∴点K在以BD为直径的圆O上运动,
∴当AK为圆O直径时,AK最大,此时点K于点C重合,
∴AK最大=AC==4,
当点C为△BEK的内心时,
BC,CE,CK分别平分∠KBE,∠BEK和∠BKE,
∴CR=CQ,
∵∠BKE=90°,
∴∠BKC=,=,
∴∠ECF=∠CBE+∠BEC,
∴点B、C、F共线,
∴BN=BC+CN=4+2=6,
∴BE===2,
∵sin∠NBE=,
∴,
∴CR=CQ=,
∴CK===,
故答案为:4,.
【点睛】本题考查了正方形的性质,全等三角形的判定和性质,确定圆的条件,解直角三角形等知识,解决问题的关键是熟练掌握有关综合知识.
三、解答题(本题有8小题,共80分.解答需写出必要的文字说明、演算步骤或证明过程)
17.(1)计算:;
(2)解方程组:.
【分析】(1)先因式分解、再通分、最后化简即可;
(2)用代入消元法解二元一次方程组即可.
【详解】解:(1)
=﹣
=﹣
=
=
=;
(2),
②×3得,3x+9y=6③,
③﹣①得,y=,
将y=代入②得,x=﹣,
∴方程组的解为.
【点睛】本题考查分式的加减、二元一次方程组的解,熟练掌握分式的化简方法,掌握代入消元法和加减消元法解二元一次方程组是解题的关键.
18.如图1是由边长为1的正方形构成的6×5的网格图,四边形ABCD的顶点都在格点上.
(1)求四边形ABCD的对角线AC的长;
(2)命题“对角线相等的四边形一定是矩形”是真命题还是假命题?如果是假命题,请在图2中画一个顶点都是格点的四边形说明;如果是真命题,请进行证明.
【分析】(1)根据勾股定理直接求解即可;
(2)对角线相等的四边形不一定是矩形,例如等腰梯形,画出图形即可.
【详解】解:(1)由题意可知,AB=4,BC=3,∠ABC=90°,
∴AC===5,
∴AC的长为5;
(2)对角线相等的四边形不一定是矩形,故命题“对角线相等的四边形一定是矩形”是假命题,如图:
在四边形ABCD中,AC=BD,但四边形ABCD为等腰梯形.
【点睛】本题主要考查命题与定理知识,熟练掌握绝对值的意义、对顶角的性质、余角的性质等知识是解题的关键.
19.如图(1)是一种迷你型可收缩式乐谱支架,图(2)是其侧面示意图,其中AB=BC=CD=24cm,DB⊥BA,Q是CD的中点,P是眼睛所在的位置,PM⊥BA于点M,AM=12cm,当PQ⊥CD时,P为最佳视力点.
(1)若∠ABC=α,则∠DCB= 2α ;
(2)当∠ABC=37°且PM=53cm时,请通过计算说明点P是不是最佳视力点.(参考数据:sin37°=cos53°≈,cos37°=sin53°≈,tan37°≈,tan53°≈)
【分析】(1)根据等腰三角形的性质以及三角形内角和定理可求出答案;
(2)通过作平行线,由(1)可求出∠C,再根据锐角三角函数的定义求出∠PQF即可.
【详解】解:(1)∵BC=CD,
∴∠CBD=∠CDB,
∵BD⊥AB,即∠ABC+∠CBD=90°,
∴∠CBD=90°﹣∠ABC
=90°﹣α,
∴∠BCD=180°﹣∠CBD﹣∠CDB
=180°﹣(90°﹣α)﹣(90°﹣α)
=2α,
故答案为:2α;
(2)如图,过点Q作EF∥AB,交PM、BD分别于F、E,则EF⊥BD,EF⊥PM,
∵∠ABC=37°,
∴∠CBD=∠CDB=90°﹣37°=53°,
∴∠DQE=∠CQF=90°﹣53°=37°,
在Rt△DEQ中,DQ=CD=12,∠EDQ=53°,
∴EQ=DQ•sinD
≈12×
=9.6,
DE=DQ•cosD
≈12×
=7.2,
∴QF=24+12﹣9.6=26.4,
过点C作CH⊥BD于H,则BH=DH,
∵Q是CD的中点,QD∥CH,
∴DE=EH,
∴BE=3DE=21.6=FM,
∴PF=53﹣21.6=31.4,
∴tan∠PQF==≈1.19≠,
∴∠PQF≠53°,
∴∠PQC=∠PQF+∠CQF≠90°,
即PQ与CD不垂直,
∴不是最佳视力点.
【点睛】本题考查解直角三角形,掌握直角三角形的边角关系是正确解答的前提,构造直角三角形是解决问题的关键.
20.某校为进一步提高教职工的身体素质,提倡“每天一万步”活动,校工会随机抽取20名教职工一天行走的步数,对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
组别
步数分组
频数
频率
A
5500≤x<6500
2
0.1
B
6500≤x<7500
10
0.5
C
7500≤x<8500
a
m
D
8500≤x<9500
3
0.15
E
9500≤x<10500
b
0.15
请根据以上信息解答下列问题:
(1)填空:a= 2 ,b= 3 ,m= 0.1 ,并补全频数分布直方图;
(2)这20名教职工一天行走步数的中位数落在 B 组;
(3)若该校教职工共有320人,请估计其中一天行走步数不少于7500步的人数.
【分析】(1)由A组频数及频率得出样本容量,再用样本容量乘以E组频率得出其频数b,根据频数之和等于总人数得出a的值,继而可得m的值;
(2)根据中位数的定义可得答案;
(3)总人数乘以样本中C、D、E组频率之和即可得出答案.
【详解】解:(1)样本容量为2÷0.1=20,
∴b=20×0.15=3,
则a=20﹣(2+10+3+3)=2,
∴m=2÷20=0.1,
补全图形如下:
故答案为:2、3、0.1;
(2)这20名教职工一天行走步数的中位数是第10、11个数据的平均数,而这两个数据均落在B组,
所以这20名教职工一天行走步数的中位数落在B组,
故答案为:B.
(3)估计其中一天行走步数不少于7500步的有320×(0.1+0.15+0.15)=128(人).
【点睛】本题考查读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
21.已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图象经过点A(﹣3,0)、B(0,3)、C(﹣2,m)三点.
(1)若点A为该函数图象的顶点,求m的值;
(2)若该函数图象关于直线x=n对称,当﹣3<n<﹣2时,m的取值范围为 ;
(3)该函数图象所经过的象限随着m值的变化而变化,写出函数图象所经过的象限及对应的m的取值范围.
【分析】(1)设抛物线为顶点式y=a(x+3)2,将B(0,3)代入,即可求解.
(2)先找到a、b的关系式,利用对称轴的范围即可求解.
(3)分类讨论,开口向上和向下两种情况.结合图象其中开口向上还要在分类讨论.
【详解】解:(1)根据题意,顶点(﹣3,0).
∴设抛物线为:y=a(x+3)2.
将B(0,3)代入,得:3=a(0+3)2.
∴a=.
∴y=(x+3)2.
当x=﹣2时,y=.
∴m=.
(2)将A(﹣3,0)、B(0,3)代入抛物线得:.
∴b=3a+1.
当x=﹣2时,m=4a﹣2b+c=4a﹣2(3a+1)+3=﹣2a+1.
抛物线的对称轴为:,则n=.
∴.
解得:.
∵m=﹣2a+1.
∴.
故答案为:.
(3)由(2)知:b=3a+1,对称轴x=.
∵二次函数中a≠0.
∴m=﹣2a+1≠1
当二次函数开口向下,即:a<0,函数图象过一、二、三、四象限,则m=﹣2a+1>1,即m>1.
当二次函数开口向上,即:a>0,此时m=﹣2a+1<1,分两种情况:
①二次函数与x轴只有一个交点,即对称轴为x=﹣3,图象经过一、二象限.
此时a=,m=﹣2a+1=.
②二次函数与x轴两个交点,即:,图象经过一、二、三象限,此时m=﹣2a+1.
综上:当m>1时,图象经过一、二、三、四象限;
当,图象经过一、二、三象限;
当m=时,图象经过一、二象限.
【点睛】本题考查待定系数法求二次函数、以及二次函数的性质、图象特征.关键在于掌握好各个知识点,加一灵活运用.
22.如图是一次药物临床试验中受试者服药后血液中的药物浓度y(微克/毫升)与用药的时间x(小时)变化的图象.第一次服药后对应的图象由线段OA和部分双曲线AB:y=组成,服药6小时后血液中的药物浓度达到最高,16小时后开始第二次服药,服药后对应的图象由线段BC和部分曲线CD:y=+m组成,其中OA与BC平行,血液中的浓度不低于5微克/毫升时有疗效.
(1)分别求受试者第16小时,第22小时血液中的药物浓度;
(2)受试者第一次服药后第二次服药前这16小时内,有疗效的持续时间达到6小时吗?
(3)若血液中的药物浓度不高于4微克/毫升时才能进行第三次服药,问受试者第二次服药后至少经过几小时可进行第三次服药?
【分析】(1)先待定系数法求出AB段和OA段的解析式,然后根据OA与BC平行,可确定BC段的解析式,然后求解即可;
(2)分别求出OA段和AB段y=5时的x的值,进一步比较即可确定;
(3)先求出CD段解析式,然后令y=4求出x的值,进一步求解即可.
【详解】解:(1)将点A(6,8)代入y=,
得k=6×8=48,
∴y=,
当x=16时,y=3,
∴B(16,3),
设OA的解析式:y=ax,
代入A(6,8),
得6a=8,
解得a=,
∴OA的解析式:y=x,
∵OA与BC平行,
设BC的解析式:y=x+b,
代入B(16,3),
得,
解得b=,
∴BC的解析式:y=x,
当x=22时,y=11,
∴C(22,11),
∴第16小时血液中的药物浓度为3微克/毫升,第22小时血液中的药物浓度为11微克/毫升;
(2)当y=x=5,解得x=,
当y==5,解得x=,
∵﹣=<6,
∴有疗效的持续时间未达到6小时;
(3)将点C(22,11)代入y=+m,
得8+m=11,
解得m=3,
∴CD段函数解析式:,
当y=4时,x=64,
∴64﹣16=48(小时),
∴受试者第二次服药后至少经过48小时可进行第三次服药.
【点睛】本题考查了反比例函数的实际应用,理解题意并求出各段的函数解析式是解题的关键.
23.如图,在正方形ABCD中,点E为线段BC上的一个动点,连结DE与对角线AC交于点F,过点A作AG∥DE,并且DG⊥AG.
(1)如图1,若AB=4,cos∠DAG=,求DF;
(2)如图2,若延长AG与CD交于点H,并延长AD至点M,连结MF,使得HD=AM,求证:MF+DF=AH;
(3)如图3,连结AE,此时将△ADF的面积记为S1,△AFE和△AEB的面积分别记为S2和S3,若S2+S3=kS1(k为常数),求k的最大值.
【分析】(1)在直角三角形ADG中,求出∠ADG(∠CDE)的正切值,进而解斜三角形CDF;
(2)作HN∥AC交FD的延长线于N,证明△DNH≌△MFA;
(3)设AB=BC=CD=AD=a,CE=x,表示出三角形CEF的面积,从而表示出S1+S2+S3和S1,从而表示出k的函数关系式,进一步得出结果.
【详解】(1)解:如图1,
作FH⊥CD于H,
∵四边形ABCD是正方形,
∴CD=AB=4,
∵∠DAC=90°,
∵∠DCF=45°,
∵DE∥AG,AG⊥DG,
∴DE⊥DG,
∴∠EDG=90°,
∴∠EDG=∠ADC,
∴∠EDG﹣∠ADE=∠ADC﹣∠ADE,
∴∠ADG=∠CDF,
∵cos∠DAG=,
∴设AG=3x,AD=5x,
∴DG=4x,
∴tan∠ADG=,
∴tan∠CDF=,
设FH=3k,DH=4k,则DF=5k,
∵tan∠DCF=,
∴tan45°=,
∴CH=3k,
由CH+DH=CD得,
∴3k+4k=4,
∴k=,
∴DF=5×=;
(2)证明:如图2,
作HN∥AC交FD的延长线于N,
∵四边形ABCD是正方形,
∴∠DAC=∠ACD=45°,
∵AG∥DB,
∴四边形AHNF是平行四边形,∠NHD=∠ACD=45°,
∴HN=AF,NF=AH,∠NHD=∠DAC,
在△DNH和△MFA中,
,
∴△DNH≌△MFA(SAS),
∴DN=MF,
∴AH=NF=DN+DF=MF+DF,
即:MF+DF=AH;
(3)如图3,
作FT⊥CD于T,作FR⊥BC,
设AB=BC=CD=AD=a,CE=x,
∴S1+S2+S3=S正方形ABCD﹣S△CDE=a2﹣,
∵AC平分∠BCD,
∴FT=FR,
∴=,
∴S△CEF=•S△CDE=,
∵BC∥AD,
∴△CEF∽△ADF,
∴=()2,
∴=,
∴S1=,
∴S1+S2=a2﹣﹣
∴k===﹣1=﹣1,
∴当x=时,k最大=.
【点睛】本题考查了正方形的性质,全等三角形的判定的性质,相似三角形的判定和性质,解直角三角形等知识,解决问题的关键是作辅助线,构造全等三角形.
24.如图1,△ABC中,BC边上的中线AM=AC,延长AM交△ABC的外接圆于点D,过点D作DE∥BC交圆于点E,延长ED交AB的延长线于点F,连接CE.
(1)若∠ACB=60°,BC=4,求MD和DF的长;
(2)①求证:BC=2CE;
②设tan∠ACB=x,=y,求y关于x的函数表达式;
(3)如图2,作NC⊥AC交线段AD于N,连接EN,当△ABC的面积是△CEN面积的6倍时,求tan∠ACB的值.
【分析】(1)利用等边三角形的判定与性质,和直角三角形的判定与性质以及圆周角定理得到点M为圆心,则结论可求;
(2)①连接BD,利用平行弦所夹的弧相等,圆周角定理,等腰三角形的性质解答即可;
②过点A作AH⊥CM于点H,通过证明△AMC∽△BMD和平行线分线段成比例定理得到y====,设CM=2a,则BM=CM=2a,利用等腰三角形的性质和勾股定理求得,代入即可得出结论;
(3)连接ME,设ME与CN交于点K,在(2)的基础上,通过证明△BDM≌△CEM和△CMN≌△CEN,利用等高的三角形的面积比等于底的比,得出AM=3DN,利用平行线分线段成比例定理可以求得=,则得到y=,IE关于x的方程即可求得结论.
【详解】(1)解:∵AM=AC,∠ACB=60°,
∴△AMC为等边三角形,
∴AM=AC=MC.
∵M是BC的中点,
∴CM=BM=BC=2.
∴AM=AC=CM=2,
∴AM=BC,
∵BM=MC,
∴△ABC为直角三角形,∠BAC=90°,
∴点M为圆心,即AD为直径,
∴DM=AM=2;
∵DE∥BC,M为AD在中点,
∴BM为△AFD的中位线,
∴FD=2BM=4;
(2)①证明:连接BD,如图,
∵DE∥BC,
∴,
∴BD=EC.
∵AM=AC,
∴∠ACM=∠AMC,
∵∠AMC=∠BMD,∠ACM=∠BDM,
∴∠BDM=∠BMD,
∴BD=BM,
∴BM=CE,
∵BC=2BM,
∴BC=2EC;
②解:过点A作AH⊥CM于点H,如图,
∵∠AMC=∠BMD,∠ACM=∠BDM,
∴△AMC∽△BMD,
∴,
∵DE∥BC,
∴.
∵CM=MB,
∴y====,
设CM=2a,则BM=CM=2a,
∵AM=AC,AH⊥CM,
∴CH=MH=a,
∵tan∠ACB=x=,
∴AH=ax,
∴AM=AC===a
∴=,
∴y==,
∴y关于x的函数表达式为:y=;
(3)连接ME,设ME与CN交于点K,如图,
∵DE∥BC,
∴,
∴,BD=EC,
∴∠CBD=∠BCE,
在△BDM和△CEM中,
,
∴△BDM≌△CEM(SAS).
∴DM=CE.
∵NC⊥AC,
∴∠MCN=90°﹣∠ACM,
∵AH⊥CM,
∴∠ACM=90°﹣∠CAH=90°﹣∠CAM,
∴∠MCN=∠CAM,
∵∠CAM=∠CBD,∠CBD=∠BCD,
∴∠MCN=∠MCE,
即:∠MCN=∠ECN,
由(2)知:CM=BM=BD,
∵CE=BD,
∴CM=CE,
在△CMN和△CEN中,
,
∴△CMN≌△CEN(SAS).
∴MN=NE.
∵CM=CE,
∴CN是ME的垂直平分线,
∴ME⊥CN,MK=KE,
∵NC⊥AC,
∴ME∥AC.
∴,
∵△ABC的面积是△CEN面积的6倍,S△ABM=S△ACM,
∴△ACM的面积是△CEN的3倍,
∵S△CEN=S△CMN,
∴△ACM的面积是△CMN的3倍,
∴AM=3MN,
∴,
∴=,
∴=,
∵ME=MD,AC=AM,
∴,
∴y=,
∴,
解得:x=,
∴tan∠ACB=x=.
【点睛】本题主要考查了圆周角定理,圆的有关性质,等腰三角形的性质,等边三角形的判定与性质,平行线分线段成比例定理,相似三角形的判定与性质,直角三角形的边角关系,勾股定理,全等三角形的判定与性质,线段的垂直平分线,熟练掌握圆的有关性质恰当的添加辅助线是解题的关键.
必刷卷04——2023年中考数学考前30天冲刺必刷卷(浙江宁波专用): 这是一份必刷卷04——2023年中考数学考前30天冲刺必刷卷(浙江宁波专用),文件包含必刷卷042023年中考数学考前30天冲刺必刷卷浙江宁波专用解析版docx、必刷卷042023年中考数学考前30天冲刺必刷卷浙江宁波专用原卷版docx等2份试卷配套教学资源,其中试卷共37页, 欢迎下载使用。
必刷卷03——2023年中考数学考前30天冲刺必刷卷(浙江温州专用): 这是一份必刷卷03——2023年中考数学考前30天冲刺必刷卷(浙江温州专用),文件包含必刷卷032023年中考数学考前30天冲刺必刷卷浙江温州专用解析版docx、必刷卷032023年中考数学考前30天冲刺必刷卷浙江温州专用原卷版docx等2份试卷配套教学资源,其中试卷共32页, 欢迎下载使用。
必刷卷03——2023年中考数学考前30天冲刺必刷卷(浙江杭州专用): 这是一份必刷卷03——2023年中考数学考前30天冲刺必刷卷(浙江杭州专用),文件包含必刷卷032023年中考数学考前30天冲刺必刷卷浙江杭州专用解析版docx、必刷卷032023年中考数学考前30天冲刺必刷卷浙江杭州专用原卷版docx等2份试卷配套教学资源,其中试卷共33页, 欢迎下载使用。












