湖南省岳阳市2022-2023学年高一数学下学期5月期中考试试题（Word版附答案）

这是一份湖南省岳阳市2022-2023学年高一数学下学期5月期中考试试题（Word版附答案），共17页。试卷主要包含了已知集合A满足，用C，若1∈{x，x2}，则x＝等内容，欢迎下载使用。

2023年岳阳县一中高一数学期中考试试题

一．选择题（共12小题）
1．已知a＞0且a≠1，若集合A＝{x|2x2＜logax}，，且A⫋B，则实数a的取值范围是（　　）
A． B．
C． D．
【分析】可求出，讨论a：0＜a＜1时，可画出y＝2x2和y＝logax的图象，根据图象可得出，从而可解出a的范围；a＞1时，可设f（x）＝2x2﹣logax，可看出当0＜x≤1时，f（x）＞0恒成立，A＝∅，从而得出a＞1时，要满足A⫋B，只需A＝∅，即对任意的x∈（0，+∞），f（x）≥0恒成立．然后通过导数可求出f（x）的最小值，然后让最小值满足，然后解出a的范围即可．
【解答】解：依题意，，且A⫋B，
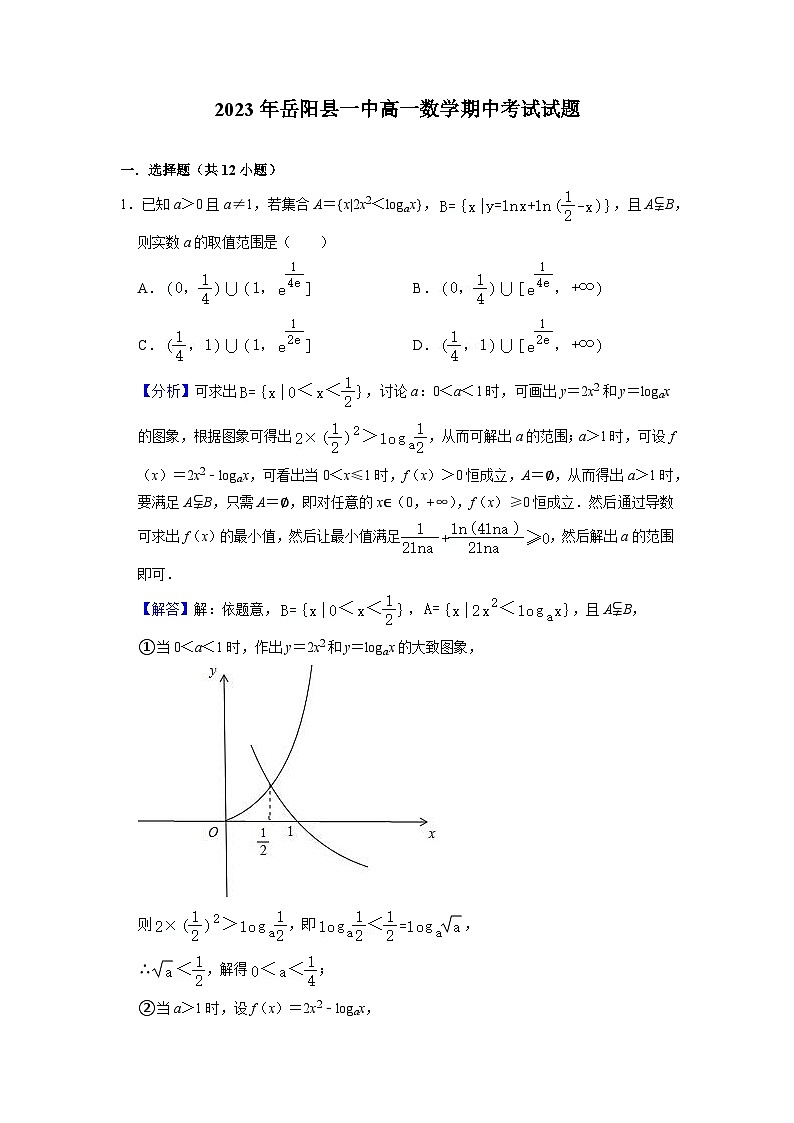
①当0＜a＜1时，作出y＝2x2和y＝logax的大致图象，

则，即，
∴，解得；
②当a＞1时，设f（x）＝2x2﹣logax，
当0＜x≤1时，logax≤0，则f（x）＞0恒成立，A＝∅，满足A⫋B，
于是当a＞1时，A⫋B，当且仅当A＝∅，即不等式f（x）≥0对∀x∈（0，+∞）恒成立，
，由f′（x）＝0得，，当时，f′（x）＜0；当时，f′（x）＞0，
∴f（x）在上单调递减，在单调递增，
∴＝，
∴，即1+ln（4lna）≥0，∴，∴，
∴当时，f（x）≥0恒成立，A＝∅，满足A⫋B，
综上得，a的取值范围为：．
故选：B．
【点评】本题考查了对数函数的定义域和单调性，借助函数图象解决函数问题的方法，对数的运算性质，对数的换底公式，根据导数求函数的最值的方法，基本初等函数的求导公式，考查了计算能力，属于难题．
2．已知集合A满足：①A⊆N，②∀x，y∈A，x≠y，必有|x﹣y|≥2，③集合A中所有元素之和为100，则集合A中元素个数最多为（　　）
A．11 B．10 C．9 D．8
【分析】根据集合A满足的条件①②可知要使得集合A中元素尽可能多，则相邻的两个自然数最少差为2，故先考虑集合中元素是由公差为2的等差数列构成，判断集合元素的个数的最多情况，再对部分元素进行调整即可得答案．
【解答】解：对于条件①A⊆N，②∀x，y∈A，x≠y，必有|x﹣y|≥2，
若集合中所有的元素是由公差为2的等差数列构成，例如{0，2，4，6，8，10，12，14，16，18，20}，集合中有11个元素，
又0+2+4+6+8+10+12+14+16+18+20＝110＞100，0+2+4+6+8+10+12+14+16+18＝90＜100，
则该集合满足条件①②，不符合条件③，故符合条件③的集合A中元素个数最多不能超过10个，
故若要集合A满足：①A⊆N，②∀x，y∈A，x≠y，必有|x﹣y|≥2，③集合A中所有元素之和为100，最多有10个元素，
例如A＝{0，2，4，6，8，10，12，15，18，25}．
故选：B．
【点评】本题主要考查元素与集合的关系，集合中元素个数最值的求法，考查运算求解能力，属于中档题．
3．用C（A）表示非空集合A中的元素个数，定义，若A＝{1，2}，B＝{x|（x2+ax）⋅（x2+ax+2）＝0}，且A*B＝1，设实数a的所有可能取值组成的集合是S，则C（S）等于（　　）
A．1 B．3 C．5 D．7
【分析】结合题意知C（A）＝2，从而可得C（B）＝1或C（B）＝3，即方程（x2+ax）•（x2+ax+2）＝0有1个根或3个根，而由x2+ax＝0得x＝0或x+a＝0，分类讨论；当a＝0时，求解集合B，判断；当a≠0时，x2+ax＝0对应的根为0和﹣a，则C（B）＝3，再按方程x2+ax+2＝0的解的情况分两类讨论，进一步检验即可．
【解答】解：由题意知，C（A）＝2，
∵A*B＝1，
A*B＝，
∴C（B）＝1或C（B）＝3，
即方程（x2+ax）•（x2+ax+2）＝0有1个根或3个根，
若（x2+ax）•（x2+ax+2）＝0，
则x2+ax＝0或x2+ax+2＝0，
若x2+ax＝0，则x＝0或x+a＝0，
当a＝0时，B＝{0}，C（B）＝1，符合题意；
当a≠0时，x2+ax＝0对应的根为0和﹣a，
若C（B）＝3，则有以下两种情况，
①当x2+ax+2＝0有两个相等的实数根时，
Δ＝a2﹣8＝0，
解得a＝±2，
当a＝2时，B＝{0，﹣，﹣2}，
C（B）＝3，符合题意；
当a＝﹣2时，B＝{0，，2}，
C（B）＝3，符合题意；
②当x2+ax+2＝0有两个不相等的实数根时，
则﹣a是x2+ax+2＝0的一个根，
即（﹣a）2+a•（﹣a）+2＝0，
无解；
综上所述，S＝{0，2，﹣2}；
故C（S）＝3，
故选：B．
【点评】本题考查了新定义的应用及分类讨论的思想方法的应用，属于中档题．
4．若1∈{x，x2}，则x＝（　　）
A．1 B．﹣1 C．0或1 D．0或1或﹣1
【分析】根据题意，若1∈{x，x2}，则必有x＝1或x2＝1，进而分类讨论：①x＝1，②x2＝1，然后求出x的值．并验证是否符合集合中元素的性质，综合即可得答案．
【解答】解：根据题意，若1∈{x，x2}，则必有x＝1或x2＝1，
进而分类讨论：
①、当x＝1时，x2＝1，不符合集合中元素的互异性，舍去，
②、当x2＝1，解可得x＝﹣1或x＝1（舍）
当x＝﹣1时，x2＝1，符合题意，
综合可得，x＝﹣1，
故选：B．
【点评】本题考查元素与集合的关系，需要注意集合中元素的互异性．
5．已知集合Rn＝{X|X＝（x1，x2，…，xn），xi∈{0，1}，i＝1，2，…，n}（n≥2）．对于A＝（a1，a2，…，an）∈Rn，B＝（b1，b2，…，bn）∈Rn，定义A与B之间的距离为d（A，B）＝|a1﹣b1|+|a2﹣b2|+…|an﹣bn|＝．
若集合M满足：M⊆R3，且任意两元素间的距离均为2，则集合M中元素个数的最大值为（　　）
A．4 B．5 C．6 D．8
【分析】由集合的子集得：R3中含有8个元素，
先阅读然后再理解定义得：可将其看成正方体的8个顶点，已知集合M中的元素所对应的点应该两两位于该正方体面对角线的两个端点，
即M＝{（0，0，0），（1，1，0），（1，0，1），（0，1，1）}或M＝{（0，0，1），（0，1，0），（1，0，0），（1，1，1）}，得解．
【解答】解：由n元子集个数得：R3中含有8个元素，可将其看成正方体的8个顶点，
已知集合M中的元素所对应的点应该两两位于该正方体面对角线的两个端点，
所以M＝{（0，0，0），（1，1，0），（1，0，1），（0，1，1）}
或M＝{（0，0，1），（0，1，0），（1，0，0），（1，1，1）}，
故集合M中元素个数最大值为4，
故选：A．
【点评】本题考查了集合的子集及阅读能力，属难度较大的题型．
6．若X是一个非空集合，M是一个以X的某些子集为元素的集合，且满足：
（1）X∈M，∅∈M；
（2）对于X的任意子集A，B，当A∈M且B∈M时，有A∪B∈M；
（3）对于X的任意子集A，B．当A∈M且B∈M时，有A∩B∈M，则称M是集合X的一个“M——集合类”．例如：M＝{∅，{b}，{c}，{b，c}，{a，b，c}}是集合X＝{a，b，c}的一个“M——集合类”．
已知X＝{a，b，c}，则所有含{b，c}的“M——集合类”的个数为（　　）
A．9 B．10 C．11 D．12
【分析】根据新定义以集合为元素组成集合，由条件可知M——集合类集合至少含有三个元素：∅，{b，c}，{a，b，c}，然后再研究其它几个元素的添加方式有多少个，可按照添加元素的个数分为0，1，2，3，4，5共六类进行讨论．
【解答】解：依题意知，M中至少含有这几个元素：∅，{b，c}，{a，b，c}，将它看成一个整体；
剩余的{a}、{b}、{c}、{a，c}、{a，b}；
①{a}、{b}、{c}、{a，c}、{a，b}5个中添加0个的集合为{∅，{b，c}，{a，b，c}}，1种，
②{a}、{b}、{c}、{a，c}、{a，b}5个中添加1个的集合为{∅，{a}，{b，c}，{a，b，c}}，{∅、{b}，{b，c}，{a，b，c}}，{∅、{c}，{b，c}，{a，b，c}}，共3种，
③{a}、{b}、{c}、{a，c}、{a，b}5个中添加2个的集合共3种，即{b}、{c}；{c}、{a，c}；{b}、{a，b}3种添加方式，
④{a}、{b}、{c}、{a，c}、{a，b}5个中添加3个的集合共4种，即{a}、{b}、{a，b}；{a}、{c}、{a，c}；{b}、{c}、{a，b}；{b}、{c}、{a，c}，4种添加方式，
⑤{a}、{b}、{c}、{a，c}、{a，b}5个中添加4个的集合共0种，
⑥{a}、{b}、{c}、{a，c}、{a，b}添加5个的集合共1种，
综上含{b，c}的“M——集合类”的个数为12种．
故选：D．
【点评】此题是一道新定义，考查元素与集合的关系，属于中档题．
7．设Q是有理数集，集合X＝{x|x＝a+b，a，b∈Q，x≠0}，在下列集合中：
①{2x|x∈X}；
②{|x∈X}；
③{|x∈X}；
④{x2|x∈X}．
与X相同的集合有（　　）
A．①② B．②③ C．①②④ D．①②③
【分析】对∀x∈X＝{x|x＝a+b，a，b∈Q，x≠0}，则∃a，b∈Q，使x＝a+b，且x≠0，则x＝2（+），从而证明X⊆{2x|x∈X}，再证明{2x|x∈X}⊆X，即可证明{2x|x∈X}＝X．故①正确；同理可证②③正确；由﹣1∈X，﹣1∉{x2|x∈X}知④错误．
【解答】解：对∀x∈X＝{x|x＝a+b，a，b∈Q，x≠0}，
∃a，b∈Q，使x＝a+b，且x≠0，则x＝2（+），
∵∈Q，∈Q，+∈X，x∈{2x|x∈X}，即X⊆{2x|x∈X}；
对∀x∈{2x|x∈X}，∃a，b∈Q，使x＝2（a+b），且x≠0，
x＝2a+2b，∵2a∈Q，2b∈Q，x≠0，∴x∈X，即{2x|x∈X}⊆X；
故{2x|x∈X}＝X．故①正确；
＝＝b+，
同理可证{|x∈X}＝X，故②正确；
＝＝﹣，
同理可证{|x∈X}＝X，故③正确；
x2＝（a+b）2＝a2+2b2+2ab，
则﹣1∈X，﹣1∉{x2|x∈X}，故④错误；
故选：D．
【点评】本题考查了集合相等的证明，通常转化为两个集合是彼此的子集证明，是中档题．
8．设集合A＝{a|∃x∈R，ax＝logax（a＞1）}，，下列说法正确的是（　　）
A．A⊆B B．B⊆A C．B⋂A＝⌀ D．B∩A≠∅
【分析】由y＝ax与y＝logax互为反函数，得到ax≤x，求出集合A；化简得到y≥，设g（x）＝，利用导数求出最值，得到集合B，由此能求出结果．
【解答】解：A＝{a|∃x∈R，ax＝logax（a＞1）}，
∵y＝ax与y＝logax互为反函数，∴∃x∈R，ax＝logax，∴只需要ax≤x，
∵a＞1，∴xlna≤lnx，∴lna≤，
设f（x）＝，得，
∴x∈（0，e）时，f′（x）＞0，f（x）单调递增，
x∈（e，+∞）时，f′（x）＜0，f（x）单调递减，
∴f（x）max＝f（e）＝，得到1＜a≤，
∴A＝（1，]，，
当x＝0时，成立；
当x＞0时，化简得y≥，设g（x）＝，
则g′（x）＝，
∵x2＞0，设h（x）＝，
则＜0，
∴h（x）单调递减，又h（0）＝0，∴当x＞0时，h′（x）＜0，h（x）＜0，
∴g′（x）＜0，g（x）单调递减，利用洛必达法则，
＝＝＝，
∴y＝g（x）≥，∴B＝[，+∞），
∴A∩B≠∅．
故选：D．
【点评】本题考查命题真假的判断，考查集合的运算法则、导数性质等基础知识，考查运算求解能力，是基础题．
9．已知集合A＝{x|x2﹣3x+2＝0}，B＝{x|0＜x＜6，x∈N}，则满足A⊆C⊆B的集合C的个数为（　　）
A．4 B．8 C．7 D．16
【分析】求出集合A＝{x|x2﹣3x+2＝0}＝{1，2}，B＝{x|0＜x＜6，x∈N}＝{1，2，3，4，5}，由此利用列举法能求出满足A⊆C⊆B的集合C的个数．
【解答】解：集合A＝{x|x2﹣3x+2＝0}＝{1，2}，
B＝{x|0＜x＜6，x∈N}＝{1，2，3，4，5}，
∴满足A⊆C⊆B的集合C有：
{1，2}，{1，2，3}，{1，2，4}，{1，2，5}，{1，2，3，4}，{1，2，3，5}，{1，2，4，5}，{1，2，3，4，5}，
共8个．
故选：B．
【点评】本题考查满足条件的集合的个数的求法，是基础题，解题时要认真审题，注意子集定义、列举法的合理运用．
10．集合M＝{x|x2﹣x＜0}，N＝{x|2x2﹣ax﹣1＜0}，M⊆N，则实数a的范围（　　）
A．（﹣∞，1] B．[1，+∞） C．（0，1） D．（﹣1，0）
【分析】本题考查集合基本运算及含参不等式的求解方法，属于中档题
【解答】解：M＝（0，1），设f（x）＝2x2﹣ax﹣1，要使M⊆N，则f（1）≤0，
所以2﹣a﹣1≤0，因此a≥1，
故选：B．
【点评】运用函数思想求解含参不等式是本题解题的关键．
11．设集合S，T中至少两个元素，且S，T满足：①对任意x，y∈S，若x≠y，则x+y∈T，②对任意x，y∈T，若x≠y，则x﹣y∈S，下列说法正确的是（　　）
A．若S有2个元素，则S∪T有3个元素
B．若S有2个元素，则S∪T有4个元素
C．存在3个元素的集合S，满足S∪T有5个元素
D．存在3个元素的集合S，满足S∪T有4个元素
【分析】不妨设S＝{a，b}，由②知集合S中的两个元素必为相反数，设S＝{a，﹣a}，由①得0∈T，由于集合T中至少两个元素，得到至少还有另外一个元素m∈T，分集合T有2个元素和多于2个元素分类讨论，即可求解．
【解答】解：若S有2个元素，不妨设S＝{a，b}，
因为T中至少有两个元素，不妨设{x，y}⊆T，
由②知x﹣y∈S，y﹣x∈S，因此集合S中的两个元素必为相反数，故可设S＝{a，﹣a}，
由①得0∈T，由于集合S中至少两个元素，故至少还有另外一个元素m∈T，
当集合T有2个元素时，由②得：﹣m∈S，则m＝±a，T＝{0，﹣a}或T＝{0，a}．
当集合T有多于2个元素时，不妨设T＝{0，m，n}，
其中m，n，﹣m，﹣n，m﹣n，n﹣m∈S，
由于m≠n，m≠0，n≠0，所以m≠﹣m，n≠﹣n，
若m＝﹣n，则n＝﹣m，但此时m﹣n＝2m≠m，m﹣n＝﹣2n≠n，
即集合S中至少有m，n，m﹣n这三个元素，
若m≠﹣n，则集合S中至少有m，n，m﹣n这三个元素，
这都与集合S中只有2个运算矛盾，
综上，S∪T＝{0，a，﹣a}，故A正确；
当集合S有3个元素，不妨设S＝{a，b，c}，
其中a＞b＜c，则{a+b，b+c，c+a}⊆T，所以c﹣a，c﹣b，b﹣a，a﹣c，b﹣c，a﹣b∈S，
集合S中至少两个不同正数，两个不同负数，即集合S中至少4个元素，与S＝{a，b，c}矛盾，排除C，D．
故选：A．
【点评】本题主要考查基于元素和集之间的关系的探究题，属于中档题．
12．如果集合S＝{x|x＝3n+1，n∈N}，T＝{x|x＝3k﹣2，k∈Z}，则（　　）
A．S⫋T B．T⊆S C．S＝T D．S⊈T
【分析】先将两集合元素表示形式统一，再比较确定包含关系．
【解答】解：由 T＝{x|x＝3k﹣2＝3（k﹣1）+1，k∈Z}＝{x|x＝3（k﹣1）+1，k﹣1∈Z}，
令 t＝k﹣1，则 t∈Z，所以 T＝{x|x＝3t+1，t∈Z}，
通过对比S、T，且由常用数集N与Z可知N⫋Z，故S⫋T．
故选：A．
【点评】本题考查了集合间包含关系的判断与应用，属基础题．
二．填空题（共3小题）
13．设集合A＝{1，2，3，4，5，6，7，8，9，10}，满足下列性质的集合称为“翔集合”：集合至少含有两个元素，且集合内任意两个元素之差的绝对值大于2．则A的子集中有 　49　个“翔集合”．
【分析】设满足题意性质的子集个数为an，则有a2＝a3＝0，a4＝1，当n＞4时，分为有n的子集和不含有n的子集，分别求解，即可得答案．
【解答】解：设集合{1，2，3，…，n}中满足题设性质的子集个数为an，则a2＝a3＝0，a4＝1，
当n＞4时，可将满足题设性质的子集分为如下两类：
一类是含有n的子集，去掉n后剩下小于n﹣2单元子集或者是{1，2，3，…，n﹣3}满足题设性质的子集，
前者有n﹣3个，后者有an﹣3个；
另一类是不含有n的子集，此时恰好是{1，2，3，…，n﹣1}满足题设性质的子集，有an﹣1个，
于是an＝（n﹣3）+an﹣3+an﹣1，
又a2＝a3＝0，a4＝1，
所以a5＝3，a6＝6，a7＝11，a8＝19，a9＝31，a10＝49．
故答案为：49．
【点评】本题属于新概念题，考查了求子集的个数，关键点在于理解“翔集合”的概念，属于中档题．
14．已知t∈R，集合A＝[t，t+1]∪[t+4，t+9]，0∉A，若存在正数λ，对任意a∈A，都有，则t的所有可能的取值组成的集合为 　{1，﹣3}　．
【分析】根据题意，分t＞0，t＜﹣9，﹣4＜t＜﹣1三种情况讨论，利用集合的包含关系列出不等式组，即可得解．
【解答】解：∵0∉A，则只需考虑下列三种情况：
①当t＞0时，a∈[t，t+1]∪[t+4，t+9]，∴，
又λ＞0，则，∵，∴且，
∴，∴λ＝t（t+9）＝（t+1）（t+4），解得t＝1；
②当t+9＜0，即t＜﹣9时，与①构造方程相同，即t＝1，不合题意，舍去；
③当，即﹣4＜t＜﹣1时，可得且，
∴λ＝t（t+1）＝（t+4）（t+9），解得t＝﹣3．
综上所述，t＝1或﹣3，
∴t的所有可能的取值组成的集合为{1，﹣3}．
故答案为：{1，﹣3}．
【点评】本题考查利用集合与元素的关系求解参数的取值问题，关键在于能够通过t的不同取值范围，得到a与所处的范围，从而能够利用集合的上下限得到关于λ的等量关系，从而构造出关于t的方程；难点在于能够准确地对t的范围进行分类，对于学生的分析和归纳能力有较高的要求，属中档题．
15．设集合A是由1，k2为元素组成的集合，则实数k的取值范围是　k≠±1　．
【分析】根据题意，由集合中元素的互异性可得k2≠1，解可得k的取值范围，即可得答案．
【解答】解：根据题意，1∈A，k2∈A，结合集合中元素的性质可知k2≠1，
解得k≠±1．
故答案为：k≠±1
【点评】本题考查集合中元素的性质，注意由集合中元素的互异性得到k2≠1．
三．解答题（共6小题）
16．集合A中的元素个数记为|A|，若M⊆A且|M|＝2，则称M为集合A的二元子集．已知集合A＝{1，2，⋯，n}（n≥3）．若对集合A的任意m个不同的二元子集A1，A2，⋯Am，均存在集合B同时满足：①B⊆A；②|B|＝m；③|B⋂Ai|≤1（1≤i≤m），则称集合A具有性质P（m）．
（1）当n＝3时，若集合A具有性质P（m），请直接写出集合A的所有二元子集以及m的一个取值；
（2）当n＝6时，判断集合A是否具有性质P（4）？并说明理由；
（3）若集合A具有性质P（2023），求n的最小值．
【分析】（1）根据集合A具有性质P（m）的定义即可得出答案；
（2）当n＝6时，利用反证法即可得出结论；
（3）首先利用反证法证明n≥2×2023﹣1＝4045，然后证明nmin＝4045，当n＝4045时，|A1|+|A2|+⋯+|A2023|＝4046＞n，再结合抽屉原理分析即可得出结论．
【解答】解：（1）当n＝3时，A＝{1，2，3}，
则集合A的所有二元子集为{1，2}，{1，3}，{2，3}，
满足题意得集合B可以是：{1}，{2}，{3}，此时m＝1，
或者也可以是{1，2}，{1，3}，{2，3}，此时m＝2；
（2）集合A不具有性质P（4），理由如下：
假设存在集合B，即对任意的A1，A2，A3，A4，|B|＝4，|B⋂Ai|≤1（1≤i≤4），
则取A1＝{1，2}，A2＝{3，4}，A3＝{5，6}，A4＝{2，3}，
此时由于|B|＝4，由抽屉原理可知，必有|B⋂Ai|＝2（2≤i≤3），
与题设矛盾，假设不成立，所以集合A不具有性质P（4）；
（3）首先证明n≥2×2023﹣1＝4045，
反证法：假设n≤2×2023﹣2＝2×2022＝4044，由集合A具有性质P（2023），
则存在集合B，对于任意A1，A2，⋯A2023，|B|＝2023，|B⋂Ai|≤1（1≤i≤2023），
则任取A1＝{1，2}，A2＝{3，4}，A3＝{5，6}，⋯，A2022＝{2×2022﹣1，2×2022}，
A2023＝{1，2×2022}，
此时由于|B|＝2023，由抽屉原理可知，必有，
与题设矛盾，假设不成立，因此n≥4045，
然后证明：nmin＝4045，
当n＝4045时，|A1|+|A2|+⋯+|A2023|＝4046＞n，
由抽屉原理可知，存在Ai∩Aj≠∅（1≤i≤j≤2023），
不妨设为A2022∩A2023≠∅，取a0∈A2022∩A2023，ai∈Ai（1≤i≤2021），
设B＝A/{a0，a1，⋯，a2021}，此时|B|≥4045﹣2022＝2023，
且|B∩Ai|≤1（1≤i≤2023），
故n＝4045符合题意，
综上所述，nmin＝4045．
【点评】本题考查学生的抽象思维能力特别是对数的分析能力，属于中档题．
17．已知A是非空数集，如果对任意x，y∈A，都有x+y∈A，xy∈A，则称A是封闭集．
（Ⅰ）判断集合B＝{0}，C＝{﹣1，0，1}是否为封闭集，并说明理由；
（Ⅱ）判断以下两个命题的真假，并说明理由；
命题p：若非空集合A1，A2是封闭集，则A1∪A2也是封闭集；
命题q：若非空集合A1，A2是封闭集，且A1∩A2≠∅，则A1∩A2也是封闭集；
（Ⅲ）若非空集合A是封闭集合，且A≠R，R为全体实数集，求证：∁RA不是封闭集．
【分析】（Ⅰ）根据封闭集的定义判断即可；
（Ⅱ）对命题p举反例A1＝{x|x＝2k，k∈Z}，A2＝{x|x＝3k，k∈Z}说明即可；
对于命题q：设a，b∈（A1∩A2），由A1，A2是封闭集，可得a+b∈（A1∩A2），ab∈（A1∩A2），从而判断为正确；
（Ⅲ）根据题意，令A＝Q，只需证明∁RQ不是封闭集即可，取∁RQ中的即可证明．
【解答】（Ⅰ）解：对于集合B＝{0}，因为0+0＝0∈B，0×0＝0∈B，
所以B＝{0}是封闭集；
对于集合C＝{﹣1，0，1}，因为﹣1+0＝﹣1∈C，﹣1×0＝0∈C，﹣1+1＝0∈C，﹣1×1＝﹣1∈C，
0+1＝1∈C，0×1＝0∈C，
所以集合C＝{﹣1，0，1}是封闭集；
（Ⅱ）解：对命题p：令A1＝{x|x＝2k，k∈Z}，A2＝{x|x＝3k，k∈Z}，
则集合A1，A2是封闭集，如A1＝{0，﹣2}，A2＝{0，3}，但A1∪A2＝{0，﹣2，3}不是封闭集，故错误；
对于命题q：设a，b∈（A1∩A2），则有a，b∈A1，又因为集合A1是封闭集，
所以a+b∈A1，ab∈A1，
同理可得a+b∈A2，ab∈A2．
所以a+b∈（A1∩A2），ab∈（A1∩A2），
所以A1∩A2是封闭集，故正确；
（Ⅲ）证明：因为非空集合A是封闭集合，且A≠R，
所以∁RA≠∅，∁RA≠R，
假设∁RA是封闭集，
由（Ⅱ）的命题q可知：若非空集合A1，A2是封闭集，且A1∩A2≠∅，则A1∩A2也是封闭集，
又因为A∩（∁RA）＝∅，
所以∁RA不是封闭集，得证．
【点评】本题考查了集合新定义的应用，属于中档题．
18．已知n为不小于3的正整数，记Ωn＝{（x1，x2，⋯，xn）|0≤x1≤x2≤⋯≤xn≤1}，对于Ωn中的两个元素X＝（x1，x2，⋯，xn），Y＝（y1，y2，⋯，yn），定义d（X，Y）为|x1﹣y1|，|x2﹣y2|，…，|xn﹣yn|中的最小值．
（Ⅰ）当n＝3时，，，，求d（X，Y）+d（Y，Z）的值；
（Ⅱ）若，为Ω3中的两个元素，且，求实数b的所有可能取值构成的集合．
（Ⅲ）若，且对于任意的X∈Ωn，均有d（A，X）≤L，求L的最小值．
【分析】（ I ） 利用定义计算即得；
（II） 根据定义和条件得到不等式组，求解即得；
（III） 先找一特例，使得，然后证明不可能更大即可．
【解答】解：（I），
，
；
（II） 若，
∴，或，
解得或，
即实数b的所有可能取值构成的集合；
（III） 若，且对于任意的X∈Ωn，均有d（A，X）≤L，
当时，，
所以．
若存在X＝{x1，x2，…，xn}∈Ωn，使得 ，
则，
∴，
∴，∴，矛盾．
所以L的最小值 ．
【点评】本题考查集合的新定义问题，关键是构造与证明相结合的思想方法，属于中档题．
19．对非空数集X，Y，定义X与Y的和集X+Y＝{x+y|x∈X，y∈Y}．对任意有限集A，记|A|为集合A中元素的个数．
（Ⅰ）若集合X＝{0，1，2}，Y＝{1，3，5，7，9}，写出集合X+X与X+Y；
（Ⅱ）若集合X＝{x1，x2，⋯，x1012}满足x1＜x2＜⋯＜x1012，且|X+X|＜2024，求|X+X|．
【分析】（Ⅰ）根据新定义列举即可求解；
（Ⅱ）根据新定义，不等式性质，即可求解．
【解答】解：（Ⅰ）∵集合X＝{0，1，2}，Y＝{1，3，5，7，9}，
∴根据题意可得：X+X＝{0，1，2，3，4}，
X+Y＝{1，2，3，4，5，6，7，8，9，10，11}；
（Ⅱ）集合X＝{x1，x2，⋯，x1012}满足x1＜x2＜⋯＜x1012，
∴x1+x1＜x1+x2＜x1+x3＜•••＜x1+x1012＜x2+x1012＜x3+x1012＜•••＜x1012+x1012，
∴X+X中至少有2×1012﹣1＝2023个元素，
即|X+X|≥2023，又|X+X|＜2024，
∴|X+X|＝2023．
【点评】本题考查新定义，不等式性质，化归转化思想，属中档题．
20．设集合A＝{5，log2（a+3）}，集合B＝{a，b}，若A∩B＝{2}，求集合B．
【分析】由题意2∈A，2＝log2（a+3），求出a，然后确定b，即可解得集合B．
【解答】解：A∩B＝{2}，∴2∈A，
又∵A＝{5，log2（a+3）}，
∴2＝log2（a+3），∴4＝a+3，∴a＝1（3分）
又∵B＝{a，b}＝{1，b}，且2∈B，∴b＝2，
∴B＝{1，2}（6分）
【点评】本题考查了集合的确定性、互异性、无序性，考查元素与集合的关系，交集的运算，属于基础题．
21．对正整数n，记In＝{1，2，3，⋯，n}，．
（1）用列举法表示集合P3；
（2）求集合P7中元素的个数；
（3）若Pn的子集A中任意两个元素之和不是整数的平方，则称A为“稀疏集”．证明：存在n使得Pn能分成两个不相交的稀疏集的并集，且n的最大值为14．
【分析】（1）由题意可得I3＝{1，2，3}，由m∈In，k∈In，可得P3＝{1，，，2，，，3，，}；
（2）对于集合P7，有n＝7．当k＝4时，根据Pn中有3个数与In＝{1，2，3…，n}中的数重复，由此求得集合P7中元素的个数．
（3）先用反证法证明证当n≥15时，Pn不能分成两个不相交的稀疏集的并集，再证P14满足要求，从而求得n的最大值．
【解答】解：（1）由题意可得I3＝{1，2，3}，
由m∈In，k∈In，
可得P3＝{1，，，2，，，3，，}；
（2）对于集合P7，有n＝7．
当k＝1时，m＝1，2，3…，7，Pn＝{1，2，3…，7}，7个数，
当k＝2时，m＝1，2，3…，7，Pn对应有7个数，
当k＝3时，m＝1，2，3…，7，Pn对应有7个数，
当k＝4时，Pn＝{|m∈In，k∈In}＝Pn＝{，1，，2，，3，}中有3个数（1，2，3）
与k＝1时Pn中的数重复，
当k＝5时，m＝1，2，3…，7，Pn对应有7个数，
当k＝6时，m＝1，2，3…，7，Pn对应有7个数，
当k＝7时，m＝1，2，3…，7，Pn对应有7个数，
由此求得集合P7中元素的个数为7×7﹣3＝46．
（3）证明：先证当n≥15时，Pn不能分成两个不相交的稀疏集的并集．假设当n≥15时，
Pn可以分成两个不相交的稀疏集的并集，设A和B为两个不相交的稀疏集，使A∪B＝Pn⊇In．
不妨设1∈A，则由于1+3＝22，∴3∉A，即3∈B．同理可得，6∈A，10∈B．又推出15∈A，
但1+15＝42，这与A为稀疏集相矛盾．
再证P14满足要求．当k＝1时，P14＝{|m∈I14，k∈I14}＝I14，可以分成2个稀疏集的并集．
事实上，只要取A1＝{1，2，4，6，9，11，13}，B1＝{3，5，7，8，10，12，14}，
则A1和B1都是稀疏集，且A1∪B1＝I14．
当k＝4时，集合{|m∈I14}中，除整数外，剩下的数组成集合{，，，…，}，
可以分为下列3个稀疏集的并：
A2＝{，，，}，B2＝{，，}．
当k＝9时，集合{|m∈I14}中，除整数外，剩下的数组成集合{，}，
可以分为下列3个稀疏集的并：
A3＝{}，B3＝{}．
最后，集合C＝{|m∈I14，k∈I14，且k≠1，4，9 }中的数的分母都是无理数，
它与Pn中的任何其他数之和都不是整数，
因此，令A＝A1∪A2∪A3∪C，B＝B1∪B2∪B3，则A和B是不相交的稀疏集，且A∪B＝P14．
综上可得，n的最大值为14．
【点评】本题主要考查新定义，集合间的包含关系，体现了分类讨论的数学思想，属于中档题．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/5/11 16:31:52；用户：杨乐；邮箱：13348702015；学号：41228115