

2023年汕头市濠江中考模拟数学试题(含答案)
展开
这是一份2023年汕头市濠江中考模拟数学试题(含答案),共10页。试卷主要包含了考生务必保持答题卡的整洁等内容,欢迎下载使用。
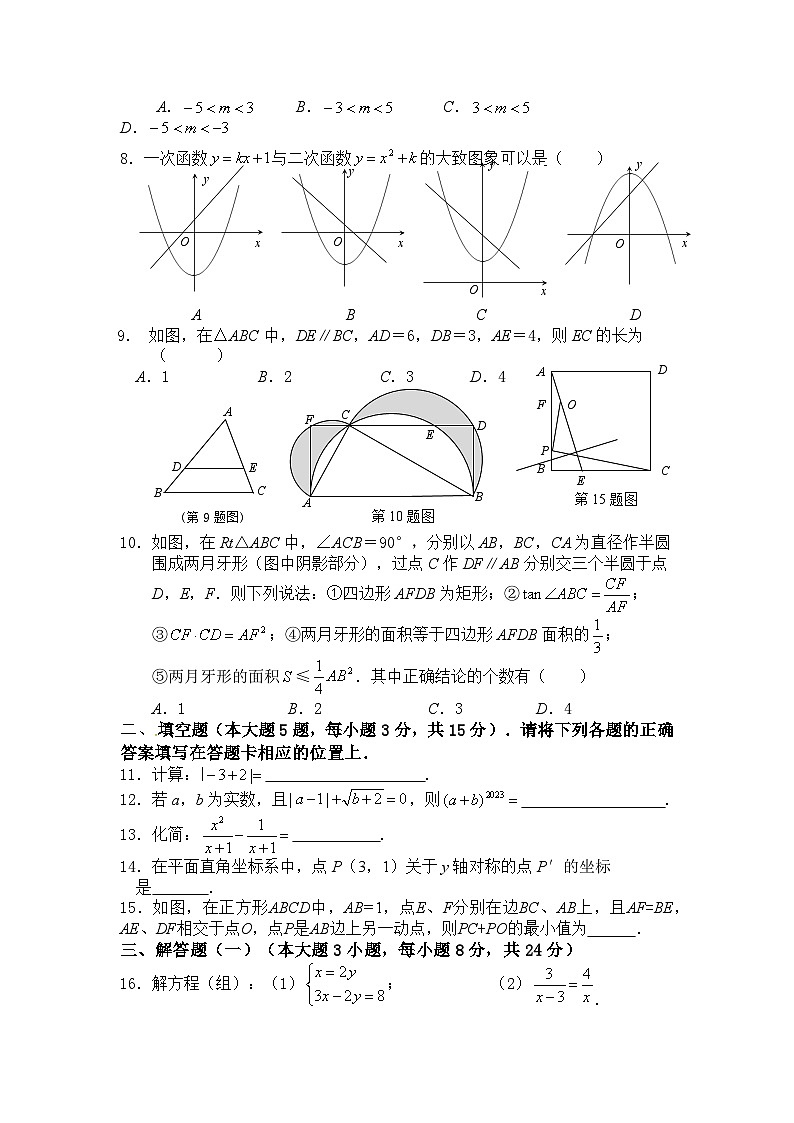
2023年九年级教学质量监测数 学说明: 1.全卷共4页,满分为120分,考试用时为90分钟.2.答卷前,考生务必用黑色字迹的签字笔或钢笔在答题卡上填写自己的准考证号、姓名、座位号.用2B铅笔把对应该号码的标号涂黑.3.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试题上.4.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔或涂改液.不按以上要求作答的答案无效.5.考生务必保持答题卡的整洁.考试结束时,将试卷和答题卡一并交回.一、选择题(本大题10题,每小题3分,共30分).在每小题列出的四个选项中,只有一个是正确的,请把答题卡上对应题目所选的选项涂黑.1.下列各数中,是负数的是( ) A.2 B.0 C. D.2.随着科学技术的不断提高,5G网络已经成为新时代的“宠儿”,预计到2025年,中国5G用户将超过460000000人,460000000用科学记数法表示为( )A.4.6×108 B.4.6×109 C.0.46×107 D.46×1073. 下列运算结果正确的是( ) A.3x3+2x3=5x6 B.(x+1)2=x2+1 C.x8÷x4=x2 D.4.如图,已知骰子相对两面的点数之和为7,下列图形为该骰子表面展开图的是( ) A. B. C. D.5.估计的值在( ) A.4和5之间 B.5和6之间 C.6和7之间 D.7和8之间6.某商场一天中卖出某种品牌的休闲鞋16双,它们的尺码与销售量如表所示:鞋的尺码/cm2525.52626.527销售量/双23443则这16双鞋的尺码组成的数据中,中位数( ) A.25.5 B.26 C.26.5 D.277.若点P在第三象限,则m的取值范围是( )A. B. C. D.8.一次函数与二次函数的大致图象可以是( ) A B C D9. 如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( ) A.1 B.2 C.3 D.4 10.如图,在Rt△ABC中,∠ACB=90°,分别以AB,BC,CA为直径作半圆围成两月牙形(图中阴影部分),过点C作DF∥AB分别交三个半圆于点D,E,F.则下列说法:①四边形AFDB为矩形;②;③;④两月牙形的面积等于四边形AFDB面积的;⑤两月牙形的面积≤.其中正确结论的个数有( )A.1 B.2 C.3 D.4二、填空题(本大题5题,每小题3分,共15分).请将下列各题的正确答案填写在答题卡相应的位置上. 11.计算: .12.若a,b为实数,且,则 .13.化简: .14.在平面直角坐标系中,点P(3,1)关于y轴对称的点P′的坐标是 .15.如图,在正方形ABCD中,AB=1,点E、F分别在边BC、AB上,且AF=BE,AE、DF相交于点O,点P是AB边上另一动点,则PC+PO的最小值为 .三、解答题(一)(本大题3小题,每小题8分,共24分)16.解方程(组):(1); (2).17.如图,四边形ABCD中,AB=BC.(1)用尺规作∠ABC的角平分线,交CD于点E;(不写作法,保留作图痕迹)(2)连接AE.求证:AE=EC.18.某校推出四种校本课程:A.象棋,B.数学游戏,C.击剑,D.趣味编程,学生可在中小学课后服务系统选择自己心仪的选修课程.为了解学生最喜欢哪一项校本课程,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:(1)这次被调查的学生共有 人;(2)请将条形统计图补充完整;(3)在平时的“趣味编程”的课堂学习中,甲、乙、丙三人表现优秀,现决定从这三名同学中任选两名参加趣味编程大赛,用树状图或列表法求出恰好同时选中甲、乙两位同学的概率. 四、解答题(二)(本大题3小题,每小题9分,共27分)19.某公司设计了一款工艺品,每件的成本是40元,为了合理定价,投放市场进行试销:据市场调查,销售单价是50元时,每天的销售量是100件,而销售单价每提高1元,每天就减少售出2件,但要求销售单价不得超过65元.(1)若销售单价为每件60元,求每天的销售利润;(2)要使每天销售这种工艺品盈利1350元,每件工艺品售价应为多少元?(3)公司每天销售这种工艺品获利能否达到2000元?请说明理由. 20.如图,直线的图象与x轴,y轴分别交于点B,A,点C在x轴上,反比例函数的图象经过菱形ABCD的顶点D.(1)求点C的坐标及反比例函数的解析式;(2)若将点C向上平移后落在反比例函数图象上的点记为点E,连接BE,DE,BD,求△BDE的面积. 21.如图1,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G. (1)线段FG与GC有何数量关系?并证明你的结论.(2)如图2,将题目中的矩形ABCD改为平行四边形ABCD,其它条件不变,(1)中的结论是否仍然成立,请说明理由.(3)如图3,连接BG,交AE于点H,若CG=DG,AB=2,请直接写出GH的长.五、解答题(三)(本大题2小题,每小题12分,共24分)22.如图,四边形ABCD是⊙O的内接四边形,AE⊥BD,BD>BC,点A是的中点,且AF∥CD.(1)若∠BAE=∠ADE,求证:BD是⊙O的直径; (2)求证:直线AF是⊙O的切线;(3)若BC=4,BE=2,求ED的长. 23.已知抛物线与x轴交于A(2,0),B(4,0)两点,与y轴交于点C,点P是抛物线一动点.(1)求抛物线的表达式;(2)如图1,当点P是第一象限内且在BC上方的动点,连接AP,交BC于点D,若DP=3AD,求点P的坐标;(3)如图2,若点P在直线BC下方的抛物线上,过点P作PQ⊥BC,垂足为Q,求的最大值. 2023年中考模拟试卷数学参考答案及评分标准一、选择题(本大题10题,每小题3分,共30分)题号12345678910答案CADDBBCBBD 二、填空题(本大题5题,每小题3分,共15分).11、 1 12、 -1 13、 x-1 14、 (-3,1) 15、 三、解答题(一)(本大题3小题,每小题8分,共24分)16、解:(1),将①代入②得:6y﹣2y=8, ………………………………1分解得y=2, ………………………………………………2分将y=2代入①得:x=4, ……………………………………3分∴原方程组的解为; ……………………………………4分解:(2)方程两边都乘x(x﹣3),得3x=4(x﹣3), ………………5分解这个方程得:x=12, ……………………………………6分经检验,x=12是原分式方程的解, …………………………7分∴原分式方程的解为x=12. ……………………………………8分 (备注:完全不给计算过程,只给答案者,每小题得1分)17、(1)解:如图所示. ………………4分(2)证明:∵BE是∠ABC的角平分线,∴∠ABE=∠CBE, ……………………5分在△ABE和△CBE中 ………6分∴△ABE≌△CBE(SAS), ……………………7分∴AE=EC ……………………8分(备注:1、画图正确得3分,下结论得1分,共4分;2、不使用全等格式,但完整给出判定条件不扣分;3、全等三角形对应点写错扣1分)18、(1)200; ……………………2分(2)选修C课程的人数为200﹣20﹣80﹣40=60(人),条形统计图补充为:……………………………4分(3)画树状图: …………6分 共有6种等可能的结果,其中同时选中甲、乙两位同学的结果数为2, …………7分所以恰好同时选中甲、乙两位同学的概率= ………………8分19、解:(1)(60﹣40)×[100﹣(60﹣50)×2]=1600(元).答:每天的销售利润为1600元. ………………………………2分(2)设每件工艺品售价为x元,则每天的销售量是[100﹣2(x﹣50)]件, ……3分依题意,得:(x﹣40)[100﹣2(x﹣50)]=1350, …………………………4分整理,得:x2﹣140x+4675=0,解得:x1=55,x2=85 ……………………5分又因为销售单价不得超过65元,故x=55. 答:每件工艺品售价应为55元. ……………………6分(3)不能,理由如下: ………………………………7分设每件工艺品售价为y元,依题意,得:(y﹣40)[100﹣2(y﹣50)]=2000 ………8分变形得,y2﹣140y+5000=0,又∵△,∴方程无实数解答:公司每天销售这种工艺品不能获利达到2000元. ………………9分(备注:1、第1小题算对单件纯利润或是销售数量其中之一,得1分,解出最后结果再得1分,共2分;2、第2小题可采用设销售单价提高x元的解法,可相应给分,本小题共4分;3、第2小题只给出其中一种结果应该相应扣1分,但如果两种结果都有却直接舍去不符合题意的一种结果则不扣分;4、第3小题可以通过求出最大利润进行解答,可相应给分,本小题3分)20、解:(1)∵直线的图象与x轴,y轴分别交于点B,A,令x=0,则y=3,∴A(0,3),令y=0,则x=﹣4,∴B(﹣4,0),∴由勾股定理可得, …………1分∵四边形ABCD是菱形,∴AD=BC=CD=AB=5 ………2分∴C(1,0) …………3分, D(5,3) …………4分∵的图象经过菱形ABCD的顶点D,∴k=5×3=15, ∴反比例函数的解析式为:; ……………5分(2)∵点C向上平移后落在反比例函数图象上, 令x=1,则y=15,∴E(1,15) ………………………………6分延长ED交x轴于点F.设直线ED的函数解析式为将E(1,15), D(5,3)代入,得,解得,∴直线ED的函数解析式为…………7分令y=0,得x=6,即F(6,0),∴………8分 ∴…………9分(第2小题可采用其他证法,本小题共4分)21、(1).理由如下:如图,连接, ………………1分∵E是的中点,∴,∵沿折叠后得到,∴,,∴, ……………………2分∵四边形是矩形,∴, ……………3分∵在和中,∵,∴,∴; ……………4分(备注:1、给出正确结论得1分;2、得到再得1分;3、得到再得1分;4、得到全等得1分)(2)解:(1)中的结论仍然成立.理由如下:如图,连接,∵E是的中点,∴,∵将沿折叠后得到,∴,,∴,∴; …………………………………………5分∵四边形为平行四边形,∴,∵,,∴, ………………………………6分∴,∴,∴…7分(3). ………………………………………………9分22、(1)解:∵AE⊥CD,∴∠AED=90°, ∴∠EAD+∠ADE=90°,……………………1分∵∠BAE=∠ADE,∴∠EAD+∠BAE=90°,即∠BAD=90° …………2分∴BD是⊙O的直径; ……………………3分(2)连接AC、AO、CO、DO∵AC是的中点,∴= ∴AC=AD …………………4分∵OC=OD,∴OA垂直平分CD ………………5分∵AF∥CD,∴ OA⊥AF …………………………………………6分又∵OA为半径,∴直线AF是⊙O的切线 …………………7分(3)在BD上截取DG=BC,连接AG,∵A是的中点,∴AC=CD.在△ABC和△AGD中,, ……………………8分∴△ABC≌△AGD(SAS), ∴AB=AG, ……………………9分又∵AE⊥BD,∴BE=GE, …………………………10分∴ED=EG+GD=BE+BC; …………………………11分∵BC=4,BE=2,∴ED=6 ………………………………12分23、解:解:(1)∵抛物线y=ax2+bx+3与x轴交于A(2,0),B(4,0)两点,∴, …………………1分,解得:, ……………2分∴抛物线的表达式为;………………3分(2)过点P作PM∥x轴,交BC于点M,如图,令x=0,则y=3, ∴C(0,3).设直线BC的解析式为y=kx+n,解得:,∴直线BC的解析式为.…………………………4分∵P(x,),∴M(,),∴PM=x=.……………………5分∵A(2,0),B(4,0),∴AB=2.∵PM∥AB,∴△PMD∽△ABD,∴, …………………………6分∵DP=3AD ∴,解得:x=6或(舍去);∴P(6,3) ………………………………7分(3)作PN⊥x轴交BC于点N,过点N作NE⊥y轴交于E,设P(m,),∴ ………8分∵PN⊥x轴 ∴PN∥OC ∴∠PNQ=∠OCB∴△PNQ∽△BCO ∴∵∴, …………9分∵△CEN∽△COB∴ ……………………………………10分∴ ……………………11分当时,的最大值是. …………………………12分
相关试卷
这是一份2023年广东省汕头市潮阳实验学校中考模拟数学试题(含解析),共22页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年广东省汕头市中考数学仿真模拟试卷(含答案),共14页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2023年广东省汕头市潮阳区潮阳区九年级中考模拟数学试题(含答案),共13页。试卷主要包含了考生务必保持答题卡的整洁,若式子有意义,则的取值范围是等内容,欢迎下载使用。









