

浙江省杭州市上城区惠兴中学2022-2023学年下学期八年级期中数学试卷 (含答案)
展开2022-2023学年浙江省杭州市上城区惠兴中学八年级(下)期中数学试卷
一.仔细选一选(本题有10个小题,每小题3分,共30分)
1.下列与杭州亚运会有关的图案中,中心对称图形是( )
A. B. C. D.
2.下列二次根式的运算正确的是( )
A. B. C. D.
3.下表是某篮球队的年龄分布,对于不同的x值,下列关于年龄的数据量不会发生改变的是( )
年龄/岁
12
13
14
15
频数
15
25
x
20﹣x
A.平均数、中位数 B.中位数、众数
C.中位数、方差 D.平均数、方差
4.用配方法解一元二次方程x2﹣8x+2=0,此方程可化为的正确形式是( )
A.(x﹣4)2=14 B.(x﹣4)2=18 C.(x+4)2=14 D.(x+4)2=18
5.若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中( )
A.至少有一个角是钝角或直角
B.没有一个角是锐角
C.每一个角都是钝角或直角
D.每一个角是锐角
6.一个多边形的内角和是其外角和的3倍,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
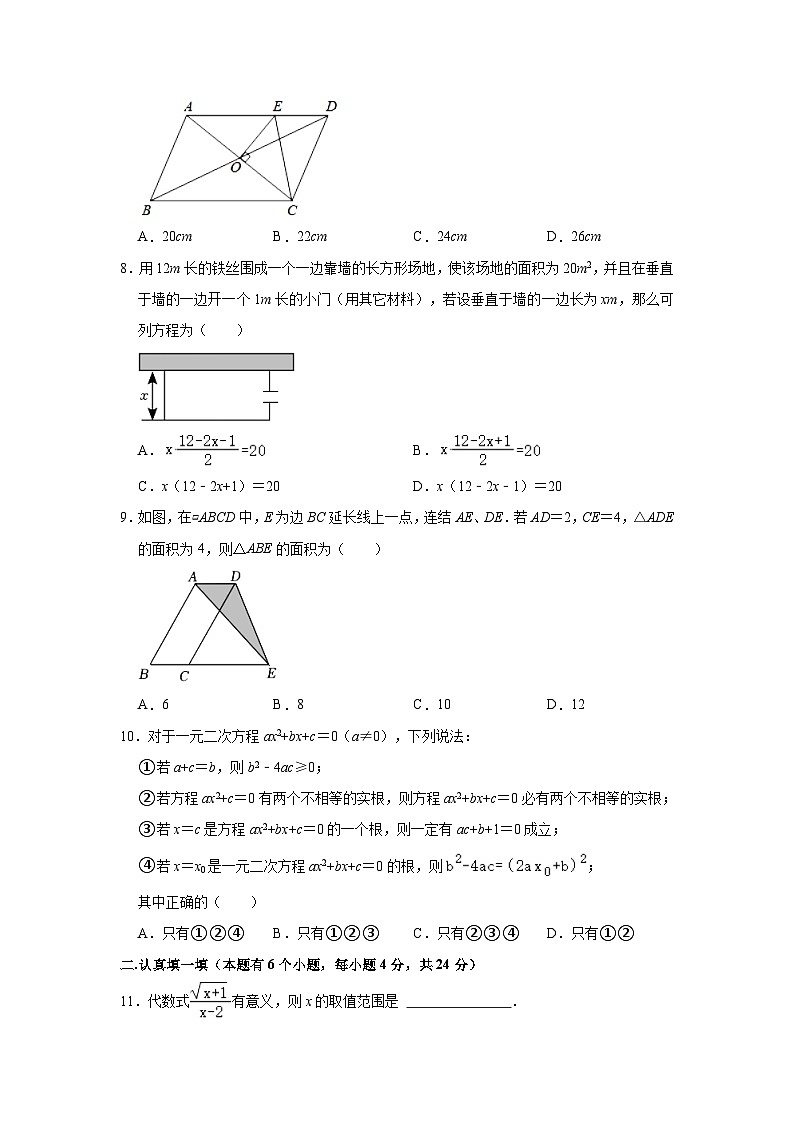
7.如图,在平行四边形ABCD,O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E,若△CDE的周长为11cm,则平行四边形ABCD的周长为( )
A.20cm B.22cm C.24cm D.26cm
8.用12m长的铁丝围成一个一边靠墙的长方形场地,使该场地的面积为20m2,并且在垂直于墙的一边开一个1m长的小门(用其它材料),若设垂直于墙的一边长为xm,那么可列方程为( )
A. B.
C.x(12﹣2x+1)=20 D.x(12﹣2x﹣1)=20
9.如图,在▱ABCD中,E为边BC延长线上一点,连结AE、DE.若AD=2,CE=4,△ADE的面积为4,则△ABE的面积为( )
A.6 B.8 C.10 D.12
10.对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若a+c=b,则b2﹣4ac≥0;
②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
③若x=c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x=x0是一元二次方程ax2+bx+c=0的根,则;
其中正确的( )
A.只有①②④ B.只有①②③ C.只有②③④ D.只有①②
二.认真填一填(本题有6个小题,每小题4分,共24分)
11.代数式有意义,则x的取值范围是 .
12.超市把a元/千克的软糖m千克,b元/千克的水果糖n千克,混合在一起,则混合后糖果的平均价格为 元/千克.
13.关于x的一元二次方程x2=a的两个根分别是2m﹣1与m﹣5,则m= .
14.如图,在▱ABCD中,∠C=68°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为 .
15.如图,水库大坝截面的迎水坡AD的坡比(DE与AE的长度之比)为4:3,背水坡BC坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,则大坝横截面的周长为 m.
16.如图,在平行四边形ABCD中,∠B=30°,AB=2,将△ABC沿AC翻折至△AB'C,连接B'D.当BC长为 时,△AB'D是直角三角形.
三.全面答一答(本题有7个小题,共66分)解答应写出文字说明,证明过程或推演步骤。如果觉得有的题目有点固难,那么把自己能写出的解答写出一部分也可以.
17.下面是小华同学解答题目的过程:
=……第一步.
=……第二步.
=……第三步.
=……第四步.
小华的解题过程是否有错误?如果有,请写出正确解答过程.
18.解方程.
(1)3x(x+1)=2(x+1);
(2)2x2﹣3x﹣5=0.
19.某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分
中位数/分
众数/分
A校
85
B校
85
100
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)若A校的方差为70分2,计算B校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
20.已知,.
(1)求x2+y2﹣xy的值;
(2)若x的小数部分是a,y的整数部分是b,求ax﹣by的值.
21.某商场一种商品的进价为每件30元,售价为每件40元.每天可销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求每次降价的百分率;
(2)经调查,若该商品每降价1元,每天可多销售8件.若每天要想获得504元的利润且尽快减少库存,每件应降价多少元?
22.如图,在▱ABCD中,∠ABC和∠DAB的角平分线BE与AE交于点E,且点E恰好在边CD上.
(1)求证:E为CD的中点;
(2)若AD=3,BE=4,求AE的长;
(3)点F为AE的中点,连接CF,交BE于点G,求证:BG=3EG.
23.如图,在▱ABCD中,AC是对角线,DE⊥AC,BF⊥AC,垂足分别为点E,F,连接BE,DF.
(1)求证:四边形DEBF是平行四边形.
(2)如图2,若▱ABCD的四个内角为90°.
①若▱ABCD两边AD:AB=1:,求证:E、F是对角线AC的三等分点.
②若四边形DEBF与▱ABCD的面积之比为k(0<k<1),请用含k的式子表示出▱ABCD的两边AB与AD的比.
参考答案
一.仔细选一选(本题有10个小题,每小题3分,共30分)
1.下列与杭州亚运会有关的图案中,中心对称图形是( )
A. B. C. D.
【分析】根据中心对称图形的定义进行判断,即可得出答案.把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.
解:选项B、C、D均不能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以不是中心对称图形,
选项A能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以是中心对称图形,
故选:A.
【点评】本题考查中心对称图形的概念:在同一平面内,如果把一个图形绕某一点旋转180度,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形.
2.下列二次根式的运算正确的是( )
A. B. C. D.
【分析】根据二次根式混合运算的法则对各选项进行逐一分析即可.
解:A、=3,原计算错误,不符合题意;
B、÷==,正确,符合题意;
C、3+=4,原计算错误,不符合题意;
D、2×5=30,原计算错误,不符合题意.
故选:B.
【点评】本题考查的是二次根式的混合运算,熟知二次根式混合运算的法则是解题的关键.
3.下表是某篮球队的年龄分布,对于不同的x值,下列关于年龄的数据量不会发生改变的是( )
年龄/岁
12
13
14
15
频数
15
25
x
20﹣x
A.平均数、中位数 B.中位数、众数
C.中位数、方差 D.平均数、方差
【分析】由频数分布表可知后两组的频数和为20,即可得知总人数,结合前两组的频数知出现次数最多的数据及第25、26个数据的平均数,可得答案.
解:由表可知,年龄为14岁与年龄为15岁的频数和为x+20﹣x=20,
则总人数为:15+25+20=50(人),
因为13岁出现的次数最多为25次,
故该组数据的众数为13岁,
第25、26个数据为13、13,
故中位数为:=13(岁),
即对于不同的x,关于年龄的统计量不会发生改变的是众数和中位数,
故选:B.
【点评】本题主要考查频数分布表及统计量的选择,由表中数据得出数据的总数是根本,熟练掌握平均数、中位数、众数及方差的定义和计算方法是解题的关键.
4.用配方法解一元二次方程x2﹣8x+2=0,此方程可化为的正确形式是( )
A.(x﹣4)2=14 B.(x﹣4)2=18 C.(x+4)2=14 D.(x+4)2=18
【分析】移项,配方,即可得出选项.
解:x2﹣8x+2=0,
x2﹣8x=﹣2,
x2﹣8x+16=﹣2+16,
(x﹣4)2=14,
故选:A.
【点评】本题考查了解一元二次方程,能够正确配方是解此题的关键.
5.若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中( )
A.至少有一个角是钝角或直角
B.没有一个角是锐角
C.每一个角都是钝角或直角
D.每一个角是锐角
【分析】反证法的步骤中,第一步是假设结论不成立,反面成立.
解:用反证法证明命题“四边形中至少有一个角是钝角或直角”时,
首先应该假设这个四边形中每一个角是锐角,
故选:D.
【点评】本题考查的是反证法,解此题关键要懂得反证法的意义及步骤.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
6.一个多边形的内角和是其外角和的3倍,则这个多边形是( )
A.七边形 B.八边形 C.九边形 D.十边形
【分析】根据多边形的外角和是360°,以及多边形的内角和定理即可求解.
解:设多边形的边数是n,则(n﹣2)•180=3×360,
解得:n=8,
故选:B.
【点评】本题考查了多边形的内角和定理以及外角和定理,正确理解定理是解题的关键.
7.如图,在平行四边形ABCD,O是AC、BD的交点,过点O与AC垂直的直线交边AD于点E,若△CDE的周长为11cm,则平行四边形ABCD的周长为( )
A.20cm B.22cm C.24cm D.26cm
【分析】由平行四边形ABCD的对角线相交于点O,OE⊥AC,根据线段垂直平分线的性质,可得AE=CE,继而可根据△CDE的周长等于AD+CD=11cm求得平行四边形的周长即可.
解:∵四边形ABCD是平行四边形,
∴OA=OC,AB=CD,AD=BC,
∵OE⊥AC,
∴AE=CE,
∵△CDE的周长为11cm,
∴△CDE的周长为:CD+CE+DE=CD+CE+AE=AD+CD=11cm.
∴▱ABCD的周长为2(AD+CD)=2×11=22厘米,
故选:B.
【点评】此题考查了平行四边形的性质,关键是根据线段垂直平分线的性质进行分析.此题难度不大,注意掌握数形结合思想的应用.
8.用12m长的铁丝围成一个一边靠墙的长方形场地,使该场地的面积为20m2,并且在垂直于墙的一边开一个1m长的小门(用其它材料),若设垂直于墙的一边长为xm,那么可列方程为( )
A. B.
C.x(12﹣2x+1)=20 D.x(12﹣2x﹣1)=20
【分析】设矩形猪舍垂直于住房墙一边长为xm可以得出平行于墙的一边的长为(12﹣2x+1)m.根据矩形的面积公式建立方程即可.
解:设矩形猪舍垂直于住房墙一边长为1m可以得出平行于墙的一边的长为(12﹣2x+1)m,由题意得x(12﹣2x+1)=20,
故选:C.
【点评】本题考查了列一元二次方程解实际问题的运用,矩形的面积公式的运用,正确寻找题目的等量关系是解题的关键.
9.如图,在▱ABCD中,E为边BC延长线上一点,连结AE、DE.若AD=2,CE=4,△ADE的面积为4,则△ABE的面积为( )
A.6 B.8 C.10 D.12
【分析】由平行四边形的性质得BC=AD=2,BC∥AD,设AD与BE之间的距离为h,再由三角形面积求出h=4,即可解决问题.
解:∵四边形ABCD是平行四边形,
∴BC=AD=2,BC∥AD,
设AD与BE之间的距离为h,
∵S△ADE=AD•h=×2•h=4,
∴h=4,
∵BE=BC+CE=2+4=6,
∴S△ABE=BE•h=×6×4=12,
故选:D.
【点评】本题主要考查了平行四边形的性质以及三角形面积,熟练掌握平行四边形的性质,求出AD与BE之间的距离是解题的关键.
10.对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若a+c=b,则b2﹣4ac≥0;
②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
③若x=c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x=x0是一元二次方程ax2+bx+c=0的根,则;
其中正确的( )
A.只有①②④ B.只有①②③ C.只有②③④ D.只有①②
【分析】①由a+b+c=0,可得出x=1是一元二次方程ax2+bx+c=0的解,进而可得出Δ=b2﹣4ac≥0;
②由方程ax2+c=0有两个不相等的实根,可得出Δ=﹣4ac>0,结合偶次方的非负性,可得出Δ=b2﹣4ac≥﹣4ac>0,进而可得出方程ax2+bx+c=0有两个不相等的实根;
③代入x=c,可得出ac2+bc+c=0,当c=0时,无法得出ac+b+1=0;
④利用求根公式,可得出x0=,变形后即可得出b2﹣4ac=(2ax0+b)2.
解:①∵a+b+c=0,
∴x=1是一元二次方程ax2+bx+c=0的解,
∴Δ=b2﹣4ac≥0,结论①正确;
②∵方程ax2+c=0有两个不相等的实根,
∴Δ=﹣4ac>0,
∴Δ=b2﹣4ac≥﹣4ac>0,
∴方程ax2+bx+c=0有两个不相等的实根,结论②正确;
③∵c是方程ax2+bx+c=0的一个根,
∴ac2+bc+c=0,
若c为0,则无法得出ac+b+1=0,结论③不正确;
④∵x0是一元二次方程ax2+bx+c=0的根,
∴x0=,
∴±=2ax0+b,
∴b2﹣4ac=(2ax0+b)2,结论④正确.
∴正确的结论有①②④.
故选:A.
【点评】本题考查了根的判别式、等式的性质以及一元二次方程的解,逐一分析四条结论的正误是解题的关键.
二.认真填一填(本题有6个小题,每小题4分,共24分)
11.代数式有意义,则x的取值范围是 x≥﹣1且x≠2 .
【分析】根据题意可得x+1≥0且x﹣2≠0,求出x的取值范围即可.
解:∵有意义,
∴x+1≥0且x﹣2≠0,
∴x≥﹣1且x≠2,
故答案为:x≥﹣1且x≠2.
【点评】本题考查二次根式的有意义的条件,熟练掌握分式有意义的条件,二次根式有意义的条件是解题的关键.
12.超市把a元/千克的软糖m千克,b元/千克的水果糖n千克,混合在一起,则混合后糖果的平均价格为 元/千克.
【分析】平均数的计算方法是求出所有数据的和,然后除以数据的总个数.
解:两种糖果的总价格为:am+bn,
混合后糖果的平均价格为=,
故答案为:.
【点评】本题考查的是加权平均数的求法.这类题目重点是确定总价格,然后用总价格除以总重量,进而求解.
13.关于x的一元二次方程x2=a的两个根分别是2m﹣1与m﹣5,则m= 2 .
【分析】利用直接开平方法解方程x2=a得到方程的两根互为相反数,则2m﹣1+m﹣5=0,则可计算出m=3即可.
解:根据题意得2m﹣1+m﹣5=0,
解得m=2,
故答案为:2.
【点评】本题考查了解一元二次方程﹣直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.
14.如图,在▱ABCD中,∠C=68°,∠DAB的平分线AE交DC于点E,连接BE.若AE=AB,则∠EBC的度数为 39° .
【分析】由平行四边形的性质得出∠C=∠DAB=68°,AB∥CD,得出∠ABC=180°﹣∠C=112°,由等腰三角形的性质和三角形内角和定理求出∠ABE=73°,即可得出∠EBC的度数.
解:∵四边形ABCD是平行四边形,
∴∠C=∠DAB=68°,AB∥CD,
∴∠ABC=180°﹣∠C=112°,
∵AE平分∠DAB,
∴∠BAE=68°÷2=34°,
∵AE=AB,
∴∠ABE=(180°﹣34°)÷2=73°,
∴∠EBC=∠ABC﹣∠ABE=112°﹣73°=39°;
故答案为:39°.
【点评】此题主要考查了平行四边形的性质,等腰三角形的性质,三角形和内角和定理等知识;关键是掌握平行四边形对边平行,对角相等.
15.如图,水库大坝截面的迎水坡AD的坡比(DE与AE的长度之比)为4:3,背水坡BC坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,则大坝横截面的周长为 (100+20) m.
【分析】过C点作CF⊥AB与点F,如图,则EF=CD=10m,CF=DE=20m,根据坡比的定义得到=,=,则可计算出AE=15m,BF=40m,再利用勾股定理计算出AD和BC,然后计算大坝横截面的周长.
解:过C点作CF⊥AB与点F,如图,则EF=CD=10m,CF=DE=20m,
∵水坡AD的坡比(DE与AE的长度之比)为4:3,
∴=,
∴AE=×20=15(m),
∴AD==25(m),
∵背水坡BC坡比为1:2,
∴=,
∴BF=2×20=40(m),
∴BC==20(m),
∴大坝横截面的周长=25+10+20+40+10+15=(100+20)m.
故答案为:(100+20).
【点评】本题考查了解直角三角形的应用﹣坡度坡角:坡度是坡面的铅直高度h和水平宽度l的比,又叫做坡比,一般用i表示,常写成i=1:m的形式.
16.如图,在平行四边形ABCD中,∠B=30°,AB=2,将△ABC沿AC翻折至△AB'C,连接B'D.当BC长为 6或4或3 时,△AB'D是直角三角形.
【分析】分两种情况,利用含30°的直角三角形的性质和全等三角形的判定和性质解答.
解:①如图1,延长B'A,交BC于点G,当∠B'AD=90°时,
∵AD=BC,BC=B'C,
∴AD=B'C,
∵AD∥BC,∠B'AD=90°,
∴∠B'GC=90°,
∵∠B=30°,AB=2,
∴∠AB'C=30°,
∴GC=B'C=BC,
∴G为BC中点,
∴BG=,
∴BC=6,
②如图2,设B'C与AD相交于点F,当∠AB'D=90°时,
∵AD=BC,BC=B'C,
∴AD=B'C,
∵AB'=AB=CD,AC=CA,
∴△ACB'≌△CAD(SSS),
∴∠DAC=∠B'CA,
∴FA=FC,
∵AD=B'C,
∴FB'=FD,
∴∠FB'D=∠FDB',
∵∠AB'C=∠B=∠CDA,
∴∠AB'D=∠CDB',
∵∠AB'D=90°,
∴∠CDB'=90°,
∴AB'∥CD,
∵AB∥CD,
∴B,A,B'在同一直线上,
∴∠BAC=∠B'AC=90°,
在Rt△ABC中,∠B=30°,AB=2,
∴BC=;
③如图3,当∠ADB′=90°时,记CD与AB′交于点O,
由折叠可知,∠B=∠ADC=∠AB′C=30°,
BC=B′C=AD,
∴∠ODB′=60°,
∵∠AOD=∠B′OC,
∴△AOD≌△COB′(AAS)
∴OD=OB′,
∴△ODB′是等边三角形,
∴∠DB′C=90°,
同理可得∠ACB′=90°,
∴∠ACB=90°,
在Rt△ABC中,∠B=30°,AB=2,
BC=AB=3.
综上所述,BC的长为6或4或3.
【点评】此题考查平行四边形的性质,关键是根据平行四边形的性质和含30°的直角三角形的性质解答.
三.全面答一答(本题有7个小题,共66分)解答应写出文字说明,证明过程或推演步骤。如果觉得有的题目有点固难,那么把自己能写出的解答写出一部分也可以.
17.下面是小华同学解答题目的过程:
=……第一步.
=……第二步.
=……第三步.
=……第四步.
小华的解题过程是否有错误?如果有,请写出正确解答过程.
【分析】根据二次根式混合运算的法则进行计算即可.
解:错误.
原式=﹣×(+3)
=﹣2×﹣2×3
=﹣2×2﹣6
=﹣4﹣6
=﹣12﹣6
=﹣.
【点评】本题考查的是二次根式的混合运算,熟知二次根式混合运算的法则是解题的关键.
18.解方程.
(1)3x(x+1)=2(x+1);
(2)2x2﹣3x﹣5=0.
【分析】(1)先移项,再利用提公因式法将方程的左边因式分解,继而得出两个关于x的一元一次方程,再进一步求解即可;
(2)利用十字相乘法将方程的左边因式分解,继而得出两个关于x的一元一次方程,再进一步求解即可.
解:(1)∵3x(x+1)=2(x+1),
∴3x(x+1)﹣2(x+1)=0,
则(x+1)(3x﹣2)=0,
∴x+1=0或3x﹣2=0,
解得x1=﹣1,x2=;
(2)∵2x2﹣3x﹣5=0,
∴(x+1)(2x﹣5)=0,
∴x+1=0或2x﹣5=0,
解得x1=﹣1,x2=.
【点评】本题主要考查解一元二次方程,解一元二次方程常用的方法有:直接开平方法、因式分解法、公式法及配方法,解题的关键是根据方程的特点选择简便的方法.
19.某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
(1)根据图示填写下表:
平均数/分
中位数/分
众数/分
A校
85
85
85
B校
85
80
100
(2)结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
(3)若A校的方差为70分2,计算B校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
【分析】(1)根据成绩表加以计算可补全统计表.根据平均数、众数、中位数的统计意义回答;
(2)根据平均数和中位数的统计意义分析得出即可;
(3)分别求出A校、B校的方差即可.
解:(1)A校平均数为:×(75+80+85+85+100)=85(分),众数85(分);
B校中位数80(分).
填表如下:
平均数/分
中位数/分
众数/分
A校
85
85
85
B校
85
80
100
故答案为:85;85;80.
(2)A校成绩好些.因为两个队的平均数都相同,A校的中位数高,
所以在平均数相同的情况下中位数高的A校成绩好些.
(3)B校的方差=×[(70﹣85)2+(100﹣85)2+(100﹣85)2+(75﹣85)2+(80﹣85)2]=160.
∴<,
因此,A校代表队选手成绩较为稳定.
【点评】本题主要考查了平均数、众数、中位数、方差的统计意义.找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;平均数是指在一组数据中所有数据之和再除以数据的个数.
20.已知,.
(1)求x2+y2﹣xy的值;
(2)若x的小数部分是a,y的整数部分是b,求ax﹣by的值.
【分析】(1)利用完全平方公式,进行计算即可解答;
(2)先估算出2﹣与2+的值的范围,从而求出a,b的值,然后代入式子中进行计算即可解答.
解:(1)∵x=2﹣,y=2+,
∴xy=(2﹣)(2+)=4﹣3=1,
(x﹣y)2=(2﹣﹣2﹣)2=(﹣2)2=12,
∴x2+y2﹣xy
=(x﹣y)2+xy
=12+1
=13;
(2)∵1<3<4,
∴1<<2,
∴3<2+<4,
∴2+的整数部分是3,
∴b=3,
∵1<<2,
∴﹣2<﹣<﹣1,
∴0<2﹣<1,
∴2﹣的整数部分是0,小数部分=2﹣﹣0=2﹣,
∴a=2﹣,
∴ax﹣by
=(2﹣)(2﹣)﹣3(2+)
=7﹣4+6﹣3
=13﹣7,
∴ax﹣by的值为13﹣7.
【点评】本题考查了二次根式的化简求值,掌握二次根式的化简方法是解题的关键.
21.某商场一种商品的进价为每件30元,售价为每件40元.每天可销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求每次降价的百分率;
(2)经调查,若该商品每降价1元,每天可多销售8件.若每天要想获得504元的利润且尽快减少库存,每件应降价多少元?
【分析】(1)设每次降价的百分率为x,根据该商品连续两次下调相同的百分率后售价降至每件32.4元,列一元二次方程,求解即可;
(2)设每件应降价y元,根据每天要想获得510元的利润,列一元二次方程,求解即可.
解:(1)设每次降价的百分率为x,
依题意得:40(1﹣x)2=32.4.
解方程得:x1=0.1=10%,x2=1.9(不合题意舍去).
答:每次降价的百分率为10%;
(2)设每件应降价y元,
依题意得:(40﹣30﹣y)(48+8y)=504
理得y2﹣4y+3=0.
解方程得:y1=1,y2=3.
要尽快减少库存,所以取y=3.
答:每天要想获得504元的利润且尽快减少库存,每件应降价3元.
【点评】本题考查了一元二次方程的应用,理解题意并根据题意建立合适的等量关系是解题的关键.
22.如图,在▱ABCD中,∠ABC和∠DAB的角平分线BE与AE交于点E,且点E恰好在边CD上.
(1)求证:E为CD的中点;
(2)若AD=3,BE=4,求AE的长;
(3)点F为AE的中点,连接CF,交BE于点G,求证:BG=3EG.
【分析】(1)由平行四边形的性质得AD=BC,AB∥CD,再∠DEA=∠BAE,再证∠DAE=∠DEA,得ED=AD,同理BC=EC,则ED=EC,即可得出结论;
(2)证∠AEB=90°,再由勾股定理即可得出结论;
(3)取BE的中点H,连接FH,由三角形中位线定理得FH∥AB,且AB=2FH,再证△CEG≌△FHG(AAS),得EG=HG,即可解决问题.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,AB∥CD,
∴∠DEA=∠BAE,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∴∠DAE=∠DEA,
∴ED=AD,
同理:BC=EC,
∴ED=EC,
∴E为CD的中点;
(2)解:由(1)可知,ED=EC=AD=3,
∴CD=2ED=6,
∵四边形ABCD是平行四边形,
∴AB=CD=6,AD∥BC,
∴∠DAB+∠ABC=180°,
∵BE平分∠ABC,AE平分∠DAB,
∴∠CBE=∠ABE=∠ABC,∠DAE=∠BAE=∠DAB,
∴∠BAE+∠ABE=∠DAB+∠ABC=(∠DAB+∠ABC)=×180°=90°,
∴∠AEB=180°﹣(∠BAE+∠ABE)=180°﹣90°=90°,
∴AE===2,
即AE的长为2;
(3)证明:如图,取BE的中点H,连接FH,
则BH=EH,
∵点F为AE的中点,
∴FH是△ABE的中位线,
∴FH∥AB,且AB=2FH,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴FH∥CD,
∴∠CEG=∠FHG,
由(1)可知,CD=2CE,
∴FH=CE,
又∵∠CGE=∠FGH,
∴△CEG≌△FHG(AAS),
∴EG=HG,
∴EH=2EG,
∵BH=EH,
∴BH=2EG=2HG,
∴BG=3EG.
【点评】本题是四边形综合题目,考查了平行四边形的性质、等腰三角形的判定、全等三角形的判定与性质、勾股定理以及三角形中位线定理等知识,本题综合性强,熟练掌握平行四边形的性质、等腰三角形的判定以及全等三角形的判定与性质是解题的关键,属于中考常考题型.
23.如图,在▱ABCD中,AC是对角线,DE⊥AC,BF⊥AC,垂足分别为点E,F,连接BE,DF.
(1)求证:四边形DEBF是平行四边形.
(2)如图2,若▱ABCD的四个内角为90°.
①若▱ABCD两边AD:AB=1:,求证:E、F是对角线AC的三等分点.
②若四边形DEBF与▱ABCD的面积之比为k(0<k<1),请用含k的式子表示出▱ABCD的两边AB与AD的比.
【分析】(1)由AAS证明△ADE≌△CBF得出BF=DE.由BF∥DE,即可得出四边形DEBF是平行四边形;
(2)①设AD=a,则CD=AB=a,由勾股定理求出AC,再求出DE、CF、EF的长,即可得出结论;
②连接BD交AC于O,证出,设OE=OF=m,则EF=2m,AC=,由勾股定理求出AD和DC的长,则可得出答案.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=CB,
∴∠DAE=∠BCF,
∵DE⊥AC,BF⊥AC,
∴DE∥BF,∠DEA=∠BFC=90°,
在△DAE和△BCF中,
,
∴△DAE≌△BCF(AAS),
∴DE=BF,
∴四边形DEBF是平行四边形;
(2)证明:∵▱ABCD的四个内角为90°,
∴四边形ABCD是矩形,
∴∠ADC=∠ABC=90°,
设AD=a,
则CD=AB=a,
∴AC===a,
∵DE⊥AC于点E,
∴DE===a,
在△ADE中,AE==a,
同理CF=a,
∴EF=AC﹣AE﹣CF=a,
∴AE=EF=CF,
即E、F是对角线AC的三等分点;
(3)解:连接BD交AC于O,
∵四边形DEBF与▱ABCD的面积之比为k,
∴,
∴,
设OE=OF=m,则EF=2m,AC=,
∴OA=OC=,
∴AE=OA﹣OE=,
由(1)可知AE=CF,
∴CE=2m+()m=,
∵四边形ABCD是矩形,
∴OD=OA=,
∴DE==,
∴DC==,
AD==,
∴=.
【点评】本题是四边形综合题,考查了平行四边形的判定与性质,全等三角形的判定与性质,矩形的判定与性质以及勾股定理等知识,熟练掌握平行四边形的判定与性质是解题的关键.
浙江省杭州市惠兴中学2023-2024学年九年级上学期期中检测数学试题: 这是一份浙江省杭州市惠兴中学2023-2024学年九年级上学期期中检测数学试题,共19页。
浙江省杭州市上城区惠兴中学2022-2023学年八年级下学期期中数学试题: 这是一份浙江省杭州市上城区惠兴中学2022-2023学年八年级下学期期中数学试题,文件包含浙江省杭州市上城区惠兴中学2022-2023学年八年级下学期期中数学试题解析版docx、浙江省杭州市上城区惠兴中学2022-2023学年八年级下学期期中数学试题原卷版docx等2份试卷配套教学资源,其中试卷共35页, 欢迎下载使用。
2022-2023学年浙江省杭州市上城区开元中学八年级(下)期中数学试卷(含解析): 这是一份2022-2023学年浙江省杭州市上城区开元中学八年级(下)期中数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












