第十三讲求与圆有关的阴影部分的面积——2022-2023学年小升初数学典型题（原卷版+解析版）

2022-2023学年小升初数学典型例题系列之

第十三讲求与圆有关的阴影部分的面积（原卷版）

编者的话：

《2022-2023学年小升初数学典型例题系列》是基于教材知识点和历年真题总结与编辑而成的，该系列主要包含典型例题和专项练习两大部分。

典型例题部分主要分为计算篇和应用篇两大篇章，每篇章皆按讲次顺序进行编辑，其优点在于考题典型，考点丰富，变式多样。

专项练习部分是从常考题和小升初真题中选取对应练习，其优点在于选题经典，题型多样，题量适中。

本专题是第十三讲求与圆有关的阴影部分的面积。本部分内容是求与圆有关的阴影部分的面积，题目综合性强，难度较大，一共划分十个考点，欢迎使用。

【考点一】求阴影部分的面积：四大基础衍生图形。

【方法点拨】

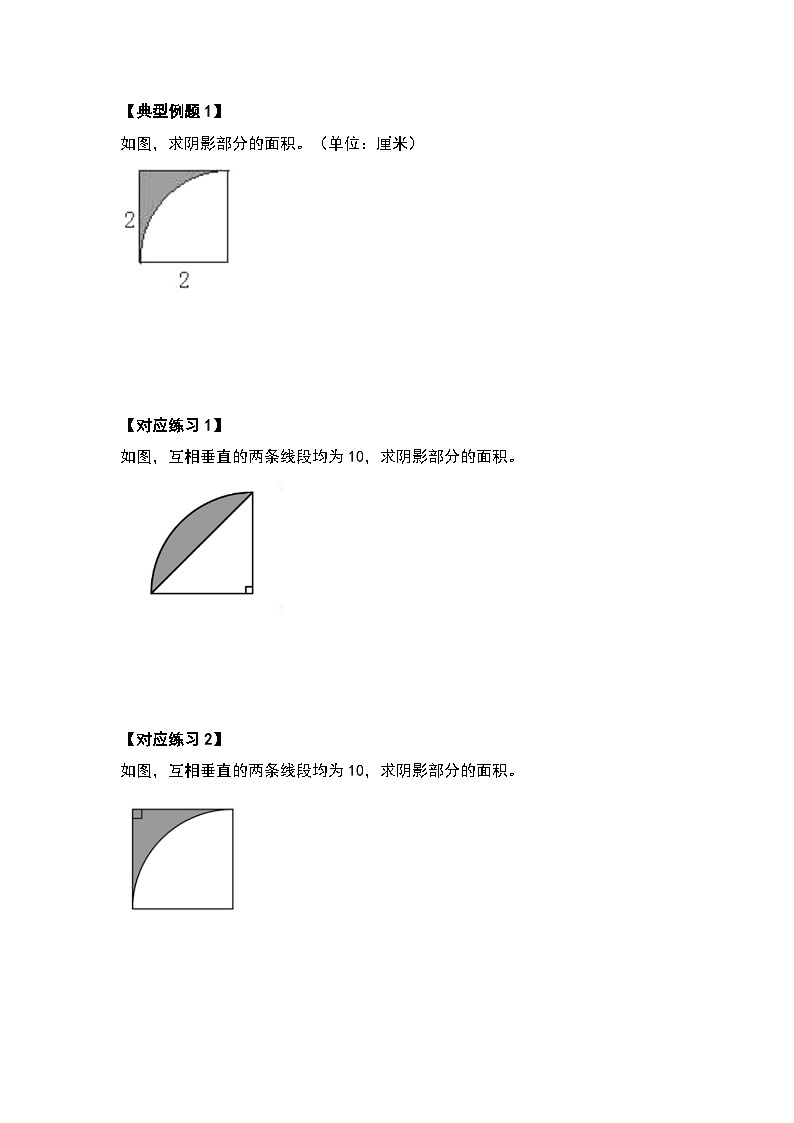
【典型例题1】

如图，求阴影部分的面积。（单位：厘米）

【对应练习1】

如图，互相垂直的两条线段均为10，求阴影部分的面积。

【对应练习2】

如图，互相垂直的两条线段均为10，求阴影部分的面积。

【对应练习3】

如图，互相垂直的两条线段均为4，求中间谷子部分的面积。

【对应练习4】

如图，求阴影部分的面积。

【考点二】求阴影部分的面积：S阴影=S1+S2。

【方法点拨】

加法分割思路是把所求阴影部分面积分割成几块能用公式计算的规则图形（三角形、正方形、长方形、平行四边形、梯形、圆、扇形），分别计算出面积，并相加得出阴影部分的面积。

【典型例题1】

如图，求阴影部分的面积。（单位：cm）

【对应练习1】

求下面图形的面积。（单位：米） 
 

【对应练习2】

计算如图的面积。
 

【考点三】求阴影部分的面积：S阴影=S整体-S空白。

【方法点拨】

减法拓展思路是把不规则图形阴影部分面积拓展到包含阴影部分的规则图形中进行分析，通过计算这个规则图形的面积和规则图形中除阴影部分面积之外多余的面积，运用“总的”减去“部分的”方法解得答案。

【典型例题1】

求阴影部分的面积。

【对应练习1】

边长为10米的正方形内的花园里，要在阴影部分种植玫瑰，种植玫瑰的面积有多大？

【对应练习2】

求阴影部分的面积。

【对应练习3】

计算下面图形中阴影部分的面积。（单位：厘米）

【考点四】求阴影部分的面积：拼接法。

【方法点拨】

在部分扇形半径相等的情况下，可以通过移动扇形，把扇形拼接成一个整体。

【典型例题】

如图，是一个边长为5厘米的等边三角形，其面积为15平方厘米，在三角形中挖去三个同样的扇形，求剩下阴影部分的面积。

 

【对应练习1】
如图，四个扇形的半径相等，求阴影部分的面积。(单位：厘米)

【对应练习2】
如图，三个扇形的半径相等，求阴影部分的面积。(单位：厘米)

【对应练习3】

如图，图中四个等圆的周长都是50.24厘米，求阴影部分的面积。

【考点五】求阴影部分的面积：割补法。

【方法点拨】

移拼、割补的思路是把不规则的阴影面积通过学习割补，使之变为一个面积大小不变且能实施计算成面积相同的规则图形。

【典型例题】

求图中阴影部分的面积（单位：厘米）。

【对应练习1】

求下面图形中阴影部分的面积（单位：厘米）。

【对应练习2】

求下面图形中阴影部分的面积（单位：厘米）

【对应练习3】

求图中阴影部分的面积（单位：厘米）。

【对应练习3】

计算下面图形中阴影部分的面积（单位：厘米，正方形边长4）。

【对应练习4】

已知右图中大正方形边长是6厘米，中间小正方形边长是4厘米，求阴影部分的面积。

【对应练习5】

有八个半径为1厘米的小圆，用它们的圆周的一部分连成一个花瓣图形(如图)。图中黑点是这些圆的圆心。如果圆周率是3.1416，那么花瓣图形的面积是多少平方厘米？

【考点六】求阴影部分的面积：圆与长方形、正方形的结合一。

【方法点拨】

注意分析长方形、正方形面积公式与圆的面积的相同之处。

【典型例题】

图中圆的周长是12.56cm，圆的面积正好等于长方形的面积，求阴影部分的面积。

【对应练习1】

图中正方形的面积是6平方厘米，求圆的面积。

【对应练习2】

已知长方形面积20平方厘米，求半圆的面积。

【对应练习3】

如图，已知阴影部分的小正方形面积是8平方分米，求图中圆的面积是多少平方分米？

【对应练习4】

如图，半圆S1的面积是14.13平方厘米，圆 S2的面积是19.625平方厘米。那么长方形(阴影部分的面积)是多少平方厘米?

【考点七】求阴影部分的面积：圆与长方形、正方形的结合二。

【方法点拨】

正方形的面积可以用对角线之积的一半来解决；长方形的面积可以看作两个三角形之和。

【典型例题】

如图，OABC是正方形，扇形的半径是6厘米，求图中阴影部分的面积？
 

【对应练习】

在图中，长方形的长是宽的2倍，半圆的面积是6.28平方厘米，求阴影部分的面积。

【考点八】求阴影部分的面积：辅助线法。

【方法点拨】

在通常手段无法求出阴影部分面积时，尝试使用添加辅助线的方法解决。

【典型例题】

ABC是等腰直角三角形。 D是半圆周的中点， BC是半圆的直径，已知AB=BC=10，那么阴影部分的面积是多少?

【考点九】求阴影部分的面积：容斥原理。

【方法点拨】

重叠、分层思路是图形中不规则的阴影部分看作几个规则图形用不同的方法重叠的结果，利用分层把重叠部分分出来，组成重叠图形各项个规则图形的面积总和减去分掉的那面积，就是剩下所求那部分面积。

【典型例题】

下图中的三角形是等腰直角三角形，阴影部分的面积是多少平方厘米？

【对应练习1】

求阴影部分的面积。（单位：厘米）

【对应练习2】

求阴影部分的面积。（单位：厘米）

【考点十】求阴影部分的面积：差不变原理。

【方法点拨】

差不变思想，即利用等式的性质来求面积：

如果S甲=S乙，那么S甲+S空白=S乙+S空白，反之亦可。

【典型例题】

如图，是一个等腰直角三角形和一个半径为4厘米、圆心角为90°的扇形拼成的图形，利用差不变思想计算下图中两个阴影部分的差是多少平方厘米？

【对应练习1】

下图中的长方形的长、宽分别是4厘米、2厘米，求阴影部分甲的面积比阴影部分乙的面积大多少平方厘米？

【对应练习2】

如图，三角形ABC是直角三角形，阴影部分甲比阴影部分乙面积大28平方厘米，AB=40厘米。求BC的长度。