第14讲 平面图形的认识与测量——2022-2023学年小升初数学基础版真题专项汇编讲义（原卷版+解析版）

基础版（通用）

2022-2023学年小升初数学精讲精练专题汇编讲义

第14讲 平面图形的认识与测量

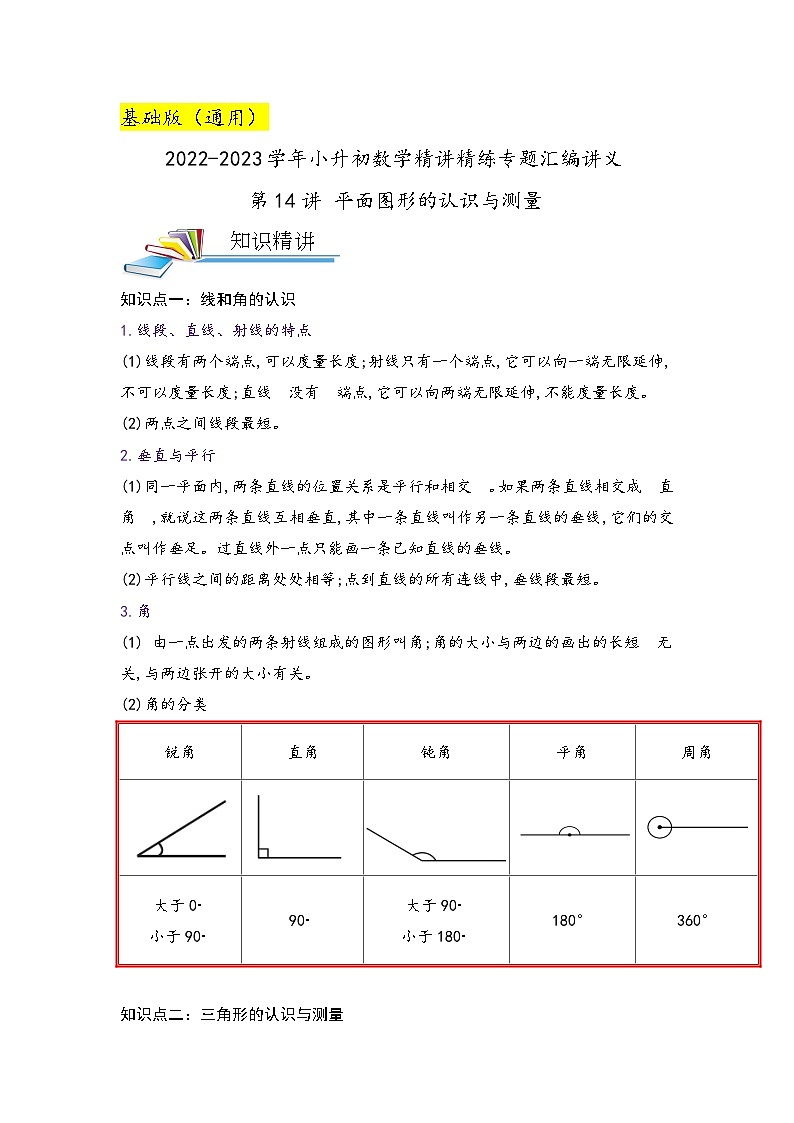
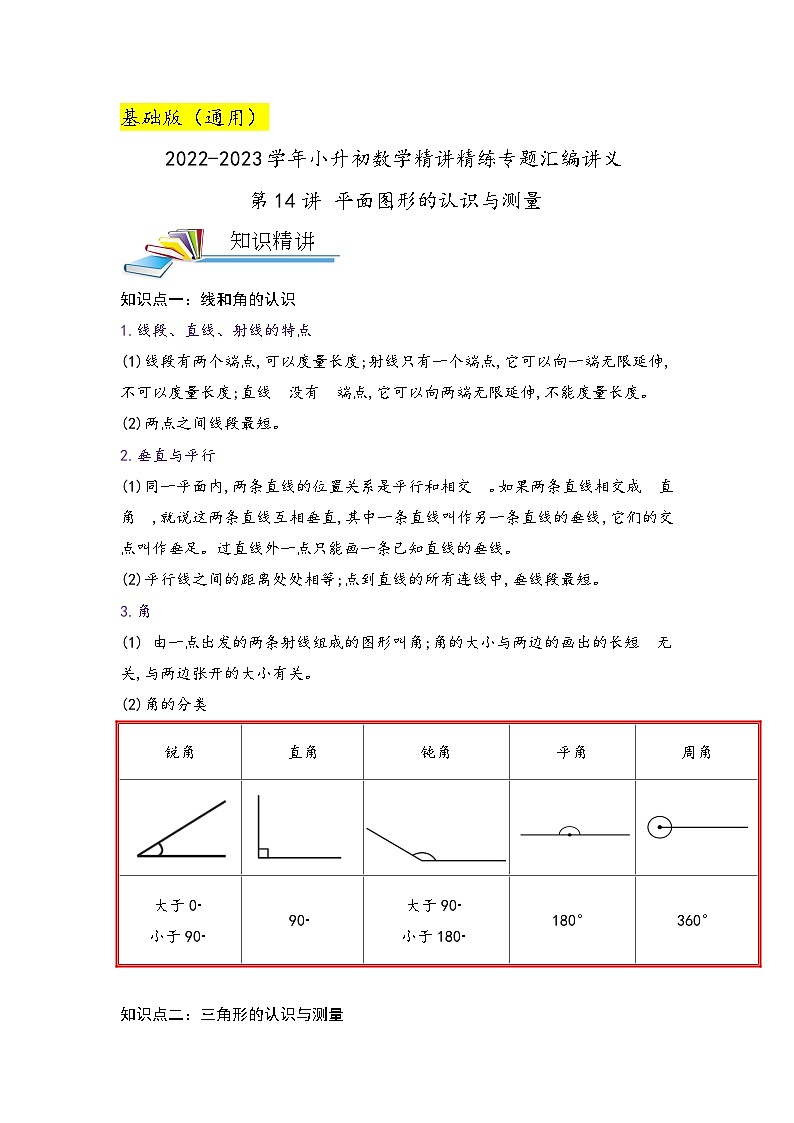
知识点一：线和角的认识

1.线段、直线、射线的特点

(1)线段有两个端点,可以度量长度;射线只有一个端点,它可以向一端无限延伸,不可以度量长度;直线　没有　端点,它可以向两端无限延伸,不能度量长度。 

(2)两点之间线段最短。 

2.垂直与平行

(1)同一平面内,两条直线的位置关系是平行和相交　。如果两条直线相交成　直角　,就说这两条直线互相垂直,其中一条直线叫作另一条直线的垂线,它们的交点叫作垂足。过直线外一点只能画一条已知直线的垂线。 

(2)平行线之间的距离处处相等;点到直线的所有连线中,垂线段最短。

3.角

(1) 由一点出发的两条射线组成的图形叫角;角的大小与两边的画出的长短　无关,与两边张开的大小有关。 

(2)角的分类

知识点二：三角形的认识与测量

1.三角形的认识

(1)三角形的特殊性质:三角形具有稳定性　。 

(2)三角形三边关系:在一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。

(3)三角形的分类:三角形按角分,分为　锐角三角形、直角三角形和钝角　三角形;按边分,分为特殊三角形和一般三角形。等腰三角形和等边三角形是特殊三角形,等边三角形是特殊的等腰三角形。 

(4)三角形的内角和是（  180° )

2.三角形的面积

两个完全一样的三角形可以拼成一个平行四边形,这个平行四边形的底就是三角形的底,所拼成平行四边形的高就是三角形的高。每个三角形的面积是所拼成平行四边形面积的一半。因为平行高四边形的面积=底×高　,所以三角形的面积=　底×高　,用字母

表示为: S=ah  。

知识点三：四边形的认识与测量

1.四边形的认识

(1)四边形的特殊性质:不稳定,易变形　 。 

(2)平行四边形两组对边分别平行且相等,梯形只有一组对边　平行　。

2.四边形的测量

(1)平行四边形的面积:平行四边形可以割补成一个长方形,这个长方形的长就是平行四边形的底　,这个长方形的宽就是平行四边形的高　,长方形的面积=长×宽,因此平行四边形的面积=底×高　,用字母表示为: S=ah　。

(2)梯形的面积:两个完全一样的梯形可以拼成一个平行四边形。这个平行四边形的底是原梯形的上底与下底之和,这个平行四边形的高是原梯形的高　。所拼成的平行四边形的面积就是（上底+下底）×高　,而原来的一个梯形的面积是拼成平行四边形面积的一半,所以梯形的面积=　(上底+下底)×高÷2　,用字母表示为:　S=(a+b)×h÷2　。

一、精挑细选(共5题；每题2分，共10分)

1．（2分）（2022六上·达川期中）一个正方形，它的一边减少一半，另一边增加1倍，则它的（　　）。 

A．面积增加，周长增加 B．面积不变，周长增加

C．面积减少，周长不变 D．面积不变，周长减少

【答案】B

【规范解答】解：假设原来正方形的边长是a，
则原来正方形的周长：a×4=4a
原来正方形的面积=a×a=a2
新的正方形的周长：
（a÷2＋a×2）×2
=（0.5a＋2a）×2
=2.5a×2
=5a
新的正方形的面积：
（a÷2）×（a×2）
=0.5a×2a
=a2
所以4a＜5a
a2=a2。
故答案为：B。

【思路点拨】正方形的周长=边长×4，正方形的面积=边长×边长，分别计算出结果后再比较大小。

2．（2分）（2022六上·灌云期中）下图中涂色部分的面积是平行四边形面积的（　　）。

A． B． C． D．

【答案】C

【规范解答】解：涂色部分的面积是平行四边形面积的。
故答案为：C。
【思路点拨】等底等高的三角形面积是平行四边形面积的一半，据此解答。

3．（2分）（2022·罗湖）一个三角形有三个锐角，其中一个角是60°，这个三角形一定是（　　）。 

A．等边三角形 B．直角三角形 C．锐角三角形 D．无法确定

【答案】C

【规范解答】解：这个三角形一定是锐角三角形。
故答案为：C。
【思路点拨】三角形的三个角都是锐角，这个三角形是锐角三角形。

4．（2分）（2022·安新）一个等腰三角形的两条边长分别是3cm和6cm，它的周长是（　　）cm。

A．9 B．15 C．12

【答案】B

【规范解答】解：3+6+6=15（cm）
故答案为：B。
【思路点拨】等腰三角形两条腰长度相等。三角形任意两边之和大于第三边，所以等腰三角形的另一条腰的长度是6cm，由此计算三角形的周长即可。

5．（2分）（2020·沈河）梯形的上下底长度比是2：3，如图，A是中点，则甲、乙面积的比是（　　）。

A．7：3 B．3：7 C．4：3 D．3：4

【答案】A

【规范解答】如图，添加辅助线：。
S△CDE：S△DEF=CD×h：EF×h=CD：EF=2：3，
所以三角形CDE的面积占2份，三角形DEF的面积占3份。
因为A是中点，所以三角形ADE和三角形AEF是等底等高的，因此三角形ADE的面积和三角形AEF的面积相等，有3÷2=1.5份。
那么，甲的面积就有2+1.5=3.5份，乙的面积有1.5份，所以3.5：1.5=7：3。
故答案为：A。

【思路点拨】梯形上下底的长度比是2：3，那么可以做辅助线，把梯形分成两个三角形，这两个三角形的高都是梯形的高，底分别是梯形的上底和下底，这样就可以推出两个三角形的面积比，再根据A是中点，利用等底等高的三角形面积相等，这样就把每个三角形占整体的份数求出来了，也就可以求出甲、乙的面积比了。

二、判断正误(共5题；每题2分，共10分)

6．（2分）（2022·八步）一个长方形的长和宽都增加6米，面积就增加36平方米。（　　）

【答案】（1）错误

【规范解答】解：假设长方形的长是a米，宽是b米
原来的面积是：ab
新的面积是：（a＋6）×（b＋6）=ab＋6a＋6b＋36
ab＋6a＋6b＋36-ab=（6a＋6b＋36）（平方米）。
故答案为：错误。
【思路点拨】假设长方形的长是a米，宽是b米，原来长方形的面积=长×宽=ab；新的面积是=（a＋6）×（b＋6）=ab＋6a＋6b＋36，然后把面积相减。

7．（2分）（2022·大余）小明说：我用11厘米，1厘米，1厘米的三根小棒围成了一个等腰三角形。（　　）

【答案】（1）错误

【规范解答】解：1＋1=2（厘米）
2厘米＜11厘米，不能围成三角形。
故答案为：错误。

【思路点拨】三角形任意两边之和大于第三边，任意两边之差小于第三边。

8．（2分）（2022·惠来）如图，在直角梯形中，阴影①的面积大于②的面积。（　　）

【答案】（1）错误

【规范解答】解：阴影①的面积=阴影②的面积。
故答案为：错误。

【思路点拨】三角形ABC和三角形BCD是等底等高的三角形，则面积相等，它们同时减去三角形③，则剩余阴影①的面积=阴影②的面积。

9．（2分）（2022·璧山）—个面积为15cm2的长方形，把它的各边放大到原来的2倍，放大后的长方形面积是30cm2。（　　）

【答案】（1）错误

【规范解答】解：15×2×2=60（cm2），所以放大后的长方形面积是60cm2。
故答案为：错误。
【思路点拨】把长方形的各边放大到原来的2倍，就是把长方形的面积扩大到原来的2×2=4倍。

10．（2分）（2021六上·霍邱期末）一个三角形三个内角的度数的比是2：3：5，它一定是直角三角形。（　　）

【答案】（1）正确

【规范解答】解：180°÷（2+3+5）×5=90°，所以它是一个直角三角形。
故答案为：正确。

【思路点拨】三角形最大的角决定三角形的特征，最大的角是锐角，那么这个三角形是锐角三角形，最大的角是直角，那么这个三角形是直角三角形，最大的角是钝角，那么这个三角形是钝角三角形；
三角形最大的角的度数=180°÷三角形三个内角占的份数和×最大的内角占的份数。

三、仔细想，认真填(共8题；每空1分，共14分)

11．（1分）（2023六上·通州期末）一个底面是正方形的长方体包装盒，高是20厘米，侧面展开后刚好是一个正方形，这个长方体包装盒的底面积是　     　平方厘米。

【答案】25

【规范解答】解：20÷4=5（厘米），5×5=25（平方厘米），所以这个长方体包装盒的底面积是25平方厘米。
故答案为：25。

【思路点拨】长方体侧面展开后刚好是一个正方形，所以长方体的高=底面正方形的周长，那么底面正方形的边长=长方体的高÷4，那么这个长方体包装盒的底面积=边长×边长。

12．（2分）（2022六上·淮滨期中）两个正方形边长的比是a：b，周长的比是　     　；面积的比是　         　。

【答案】a：b；：

【规范解答】解：边长的比是a：b，周长的比是a：b；面积的比是：。
故答案为：a：b；：。

【思路点拨】正方形的边长比、周长比都相等，面积比等于边长的平方的比。

13．（1分）（2022六上·崂山期中）一个长方形的周长是36厘米，长与宽的比是5：4，这个长方形的面积是　     　平方厘米。

【答案】80

【规范解答】解：36÷2=18（厘米）
18÷（5+4）=18÷9=2（厘米）
5×2=10（厘米），4×2=8（厘米），
10×8=80（平方厘米）
故答案为：80。
【思路点拨】长方形的周长÷2=长方形的长宽之和，长方形的长宽之和÷总份数=一份的长度，一份的长度×5=长方形的长，一份的长度乘4=长方形的宽，长方形的长×长方形的宽=长方形的面积。

14．（2分）在一个周长是32 厘米的正方形铁板内，要割下一个最大的圆，这个圆的面积是　     　平方厘米，剩下铁板的面积是　     　平方厘米。

【答案】50.24；13.76

【规范解答】解：32÷4=8厘米，（8÷2）2×4.14=50.24平方厘米，所以这个圆的面积是50.24平方厘米，8×8-50.24=13.76平方厘米，所以剩下铁板的面积是13.76平方厘米。
故答案为：50.24；13.76。
【思路点拨】在正方形内割一个最大的圆，圆的直径=正方形的边长，正方形的边长=正方形的周长÷4，所以割下的圆的面积=（直径÷2）2×π；正方形的面积=边长×边长，所以剩下铁板的面积=正方形的面积-割下的圆的面积。

15．（2分）如图，一张长方形纸的长是24 厘米，在这张纸上正好画了一个半圆，长方形的面积是　     　平方厘米，半圆形的面积是　     　平方厘米。

【答案】288；226.08

【规范解答】解：24÷2=12厘米，24×12=288平方厘米，所以长方形的面积是288平方厘米，122×3.14÷2=226.08平方厘米，所以半圆的面积是226.08平方厘米。
故答案为：288；226.08。
【思路点拨】从图中可以看出，半圆的直径=长方形的长，半圆的半径=长方形的宽，那么长方形的面积=长×宽；半圆的面积=半径2×π÷2。

16．（2分）一个等腰三角形的两个角度数比是1：2，这个三角形的顶角可能是　     　度或　     　度。

【答案】90；36

【规范解答】解：180÷（1＋1＋2）
=180÷（2＋2）
=180÷4
=45（度）
45×2=90（度）
180÷（2＋2＋1）
=180÷（4＋1）
=180÷5
=36（度）
故答案为：90；36。
【思路点拨】这个三角形顶角的度数=三角形的内角和÷总份数×顶角占的份数。

17．（3分）（2022·磐石）如图。∠1＝30°，∠2＝　     　，∠3＝　     　，∠4＝　     　。

【答案】150°；30°；150°

【规范解答】解：∠2＝180°-30°=150°，∠3＝30°，∠4＝150°。
故答案为：150°；30°；150°。

【思路点拨】从图中可以看出，∠1=∠3，∠2=∠4，∠1+∠2=180°，据此作答即可。

18．（1分）（2022·滁州）如图所示，已知涂色三角形②的面积是16cm2，梯形①的面积是　     　cm2。

【答案】80

【规范解答】解：高：16×2÷4=8（cm）；
梯形①的面积：
（12-4+12）×8÷2
=20×8÷2
=80（cm2）
故答案为：80。

【思路点拨】根据三角形面积公式用三角形②的面积乘2再除以底的长度即可求出三角形的高，也就是梯形的高。然后用梯形①的上底和下底的和乘高再除以2即可求出梯形面积。

四、解答问题(共12题；共66分)

19．（5分）（2022·海沧）一个三角形中最小的角是44°，这个三角形可能是哪类三角形？请说明理由。

【答案】解：假设剩下的两个角中的一个角也是44°，所以另一个角为：180°﹣44°﹣44°＝92°，即为钝角三角形；假设剩下的两个角中的一个角是46°，所以另一个角为：180°﹣44°﹣46°＝90°，即为直角三角形；假设剩下的两个角中的一个角是89°，所以另外一个角的度数是：180°﹣44°﹣89°＝47°，即为锐角三角形。所以这个三角形可能是钝角三角形，可能是直角三角形，也可能是锐角三角形。

【思路点拨】三角形按照角的大小分为三类：钝角三角形（有一个角大于90°小于180°）、直角三角形（有一个角等于90°）、锐角三角形（三个角都大于0°小于90°）；本题即是根据角的特点分别计算，即已知最小的角是44°，那么剩下的两个角中的一个角若等于44°，计算出另外一个角，判断三角形的形状；接下来看44°和多少度组成直角，即可得出直角三角形；最后最大的锐角是89°（按整数算），计算出另外一个角的度数，即可得出答案。

20．（5分）（2022·惠州）一块平行四边形的菜地，用1：2000的比例尺画在图上，底3厘米，高2厘米。这块菜地的实际面积是多少平方米？

【答案】解：3÷ ＝6000（厘米）

6000厘米＝60米

2÷ ＝4000（厘米）

4000厘米＝40米

60×40＝2400（平方米）

答：这块菜地的实际面积是2400平方米。

【思路点拨】菜地实际的底=图上的底÷比例尺，菜地实际的高=图上的高÷比例尺，然后进行单位换算，即1米=100厘米，所以这块菜地的实际面积=菜地实际的底×菜地实际的高，据此代入数字作答即可。

21．（5分）一根铁丝恰好可以围成一个直径为4dm的圆，若将这根铁丝恰好围成一个正方形，围成的正方形的面积是多少平方分米？

【答案】解：4×3.14=12.56（分米）
12.56÷4=3.14（分米）
3.14×3.14=9.8596（平方分米）
答：围成的正方形的面积是9.8596平方分米。

【思路点拨】铁丝的长度=圆的直径×π，所以正方形的边长=铁丝的长度÷4，正方形的面积=边长×边长，据此代入数值作答即可。

22．（5分）（2022·璧山）如图阴影部分的面积是6cm2，求出梯形的面积。

【答案】解：6×2÷4

＝12÷4

＝3（厘米）

（2+4）×3÷2

＝6×3÷2

＝18÷2

＝9（平方厘米）

答：梯形的面积是9平方厘米。

【思路点拨】从图中可以看出，梯形的面积=（上底+下底）×高÷2，梯形的高=阴影部分三角形的面积×2×阴影部分三角形的底，据此作答即可。

23．（5分）一位居住在西班牙的古巴画家创作了世界上最大的头像画，画长120米，宽比长短 ，这幅画像的面积是多少平方米？

【答案】解：120×（1- ）×120
=120××120
=80×120
=9600（平方米）

答：这幅画像的面积是9600平方米。

【思路点拨】画的长×（1-）=画的宽，画的长×画的宽=画的面积。

24．（5分）（2022六下·同江期中）某建筑工地要挖一个长方形地基，把它画在比例尺是1∶500的平面图上，长是12厘米，宽是5厘米，这块地基的实际面积是多少平方米？

【答案】解：12÷=12×500=6000（厘米）=60（米）；
5÷=5×500=2500（厘米）=25（米）；
60×25=1500（平方米）
答：这块地基的实际面积是1500平方米。

【思路点拨】实际距离=图上距离÷比例尺，据此算出长方形的长和宽；长方形的长×宽=这块地基的实际面积。

25．（6分）（2022六下·莘县期中）在比例尺为1：100的基建图纸上，量得教室的长是8厘米，宽是5.5厘米，这间教室的实际面积是多少平方米？

【答案】解：实际长：8×100=800（厘米）
实际宽：5.5×100=550（厘米）
800厘米=8米
550厘米=5.5米
实际面积：8×5.5=44（平方米）
答：这间教室的实际面积是44平方米。

【思路点拨】1：100表示图上1厘米是实际的100厘米，8厘米就是8个100厘米， 5.5厘米就是5.5个100厘米，这样就可以求出实际的长和宽，从而计算出实际面积，注意单位。

26．（6分）李大名用篱笆围一块梯形菜地，一面靠墙(如图所示)，篱笆全长40米，如果每平方米收白菜10.5千克，那么这块地一共可以收白菜多少千克？

【答案】解：(40-14)×14÷2
=26×14÷2
=364÷2
=182(平方米)

182×10.5=1911(千克)

答：一共可以收白菜1911千克。

【解析】【思路点拨】一共可以收白菜的质量=梯形菜地的面积×平均每平方米收白菜的质量；其中，梯形菜地的面积=（上底＋下底）×高÷2，上底＋下底=篱笆全长 -高。

27．（6分）如图所示，求∠1，∠2的度数。

【答案】解：∠1=180°-130°=50°

∠2=180°-65°-50°=65°

答：∠1为50°，∠2为65°。

【思路点拨】∠1=平角-130°；∠2=三角形的内角和-∠1-∠B。

28．（6分）从一张正方形纸上剪下一个周长是18.84厘米的最大圆，求被剪掉的纸屑的面积。

【答案】解：半径：18.84÷3.14÷2=3(厘米)，边长：3×2=6(厘米)，剪掉的面积：6×6-3.14×3²=36-28.26=7.74(平方厘米)答：被剪掉的纸屑面积是7.74平方厘米。

【思路点拨】这个圆的直径就是正方形的边长，用圆的周长除以3.14再除以2求出半径，然后计算出正方形的边长，用正方形面积减去圆面积就是剪掉的纸屑的面积。

29．（6分）一个正方形边长扩大后，面积扩大为原来的9倍，扩大后正方形的边长为12厘米。这个正方形原来的边长是多少厘米？

【答案】解：12×12=144(平方厘米)，144÷9=16(平方厘米)，16=4×4

答：这个正方形原来的边长是4厘米。

【思路点拨】用扩大后正方形的边长乘边长求出扩大后的面积，用扩大后的面积除以9求出原来的面积，然后根据正方形面积公式判断原来正方形的边长即可。

30．（6分）（2019六上·东源期中）一根铁丝可以围成一个直径是6cm的圆，如果用它围成一个等边三角形，每边的长是多少厘米?

【答案】铁丝的长度：3.14×6=18.84（厘米）；
等边三角形的边长：18.84÷3=6.28（厘米）.
答： 如果用它围成一个等边三角形，每边的长是6.28厘米.

【思路点拨】根据题意可知，先求出这根铁丝的长度，用圆的周长公式：C=πd，然后用铁丝的长度÷3=围成的等边三角形的边长，据此列式解答.