人教版八年级下册19.2.1 正比例函数备课ppt课件

这是一份人教版八年级下册19.2.1 正比例函数备课ppt课件，共19页。PPT课件主要包含了解13，y2x，②描点，③连线，y-15x，y-4x，相同点，都是经过原点的直线，不同点，解列表如下等内容，欢迎下载使用。

1.理解正比例函数的图象的特点，会利用两点(法)画正比例函数的图象.2.掌握正比例函数的性质，并能灵活运用性质解答有关问题.
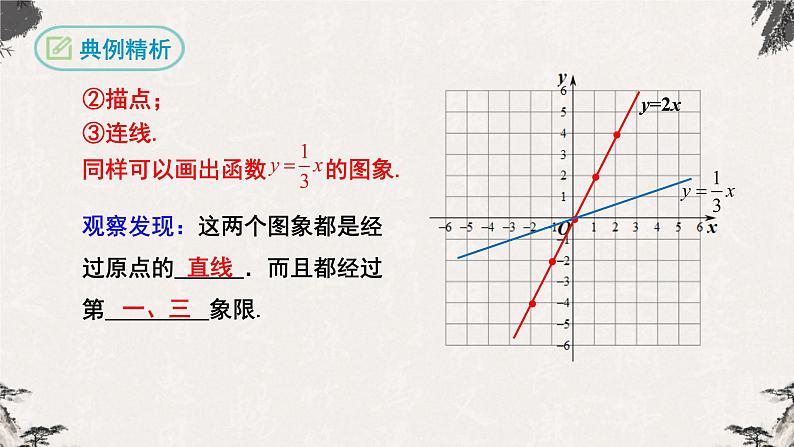
2.描点法画函数图象的三个步骤是______、______、______.
1.下列函数哪些是正比例函数？ （1）y=-3x ； （2）y=x+3； （3）y=4x； （4）y=x2.
解:(1)函数y=2x中自变量x可为任意实数.①列表如下：
观察发现：这两个图象都是经过原点的 ．而且都经过第 象限.
解:(2)函数y=-1.5x中自变量x可为任意实数.①列表如下：
同样可以画出函数y=-4x的图象.
比较这几个正比例函数图象，它们有什么相同点和不同点？
当k＞0时，它的图象经过第 象限.
当k＜0时，它的图象经过第 象限.
从左到右图象上升；x增大时，y的值也增大，即y随x的增大而增大.
从左到右图象下降；x增大时，y的值反而减小，即y随x的增大而减小.
①当k＞0时，直线y=kx经过第一、三象限，y随x的增大而增大；②当k＜0时，直线y=kx经过第二、四象限，y随x的增大而减小.
正比例函数y=kx(k是常数且k≠0) 的图象是经过原点的一条直线. 函数y=kx的图象我们也称作直线y=kx .
正比例函数的图象及性质：
3.已知正比例函数y=2x的图象上有两点（3，y1），（5，y2），则y1 y2.4.已知正比例函数y=kx(k<0)的图象上有两点（-3，y1），（1，y2），则y1 y2.
1.已知正比例函数y=mx的图象经过点（m，4），且y的值随着x值的增大而减小，求m的值.
解：∵正比例函数y=mx的图象经过点（m，4）, ∴4=m·m，解得m=±2. ∵y的值随着x值的增大而减小， ∴m<0，故m=-2
1.已知y-3与2x-1成正比例，且x=1时，y=6. (1)求y与x之间的函数关系式； (2)如果y的取值范围是0≤y≤30 ，求x的取值范围.
解：(1)根据题意，设y-3=k(2x-1) 将x=1， y=6代入解得：k=6 . ∴y-3=6(2x-1)，即y=6x . (2)因为k=6＞0，所以y随x的增大而增大. 又当y=0时，x=0；当y=30时，x=5 . ∴x的取值范围是0≤x≤5.
正比例函数的概念和解析式.函数y=kx（k是不等于零的常数）叫做正比例函数. k为比例系数.可用已知的比例系数求解析式或用待定系数法求解析式
正比例函数的图象.正比例函数的图象是经过原点的一条直线
正比例函数的性质. 当k＞0时，直线y=kx经过第一、三象限，y随x的增大而增大；当k＜0时，直线y=kx经过第二、四象限，y随x的增大而减小
1.已知函数y=kx经过二、四象限，且函数不经过（-1，1），请写出一个符合条件的函数解析式 .
解：∵函数y=kx经过二、四象限， ∴k＜0． 若函数y=kx经过（-1，1），则1=- k，即k=-1， 故函数y=kx经过二、四象限，且函数不经过（-1，1）时，k＜0且k≠-1， ∴函数解析式为y=-2x，
y=-2x（答案不唯一）
2.已知y与x-4成正比例，且当x=2时，y=-6，则当y=9时，求x的值.
解：根据题意，设y=k(x-4) 将x=2，y=-6代入解得k=3 ∴y=3(x-4) 将y=9代入上式，解得：x=7.