2023届高考数学二轮复习专题十一空间点、线、面的位置关系作业（A）含答案

这是一份2023届高考数学二轮复习专题十一空间点、线、面的位置关系作业（A）含答案，共14页。试卷主要包含了下列说法正确的是等内容，欢迎下载使用。
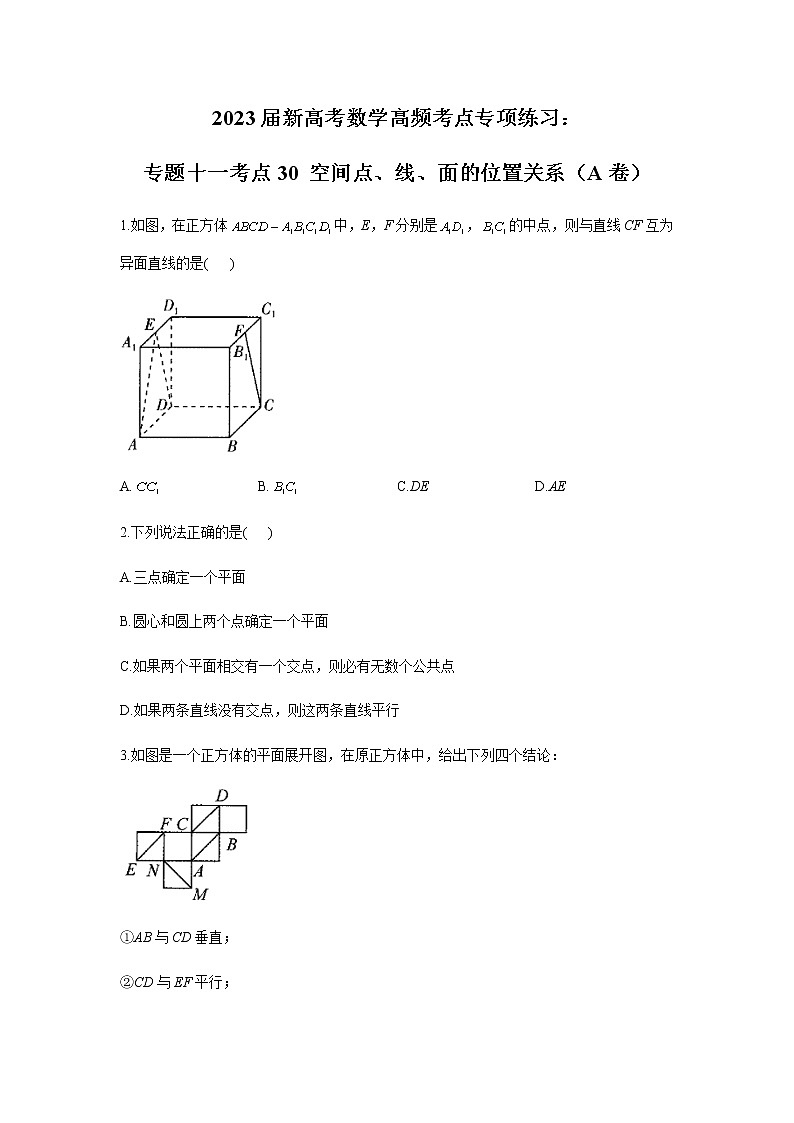
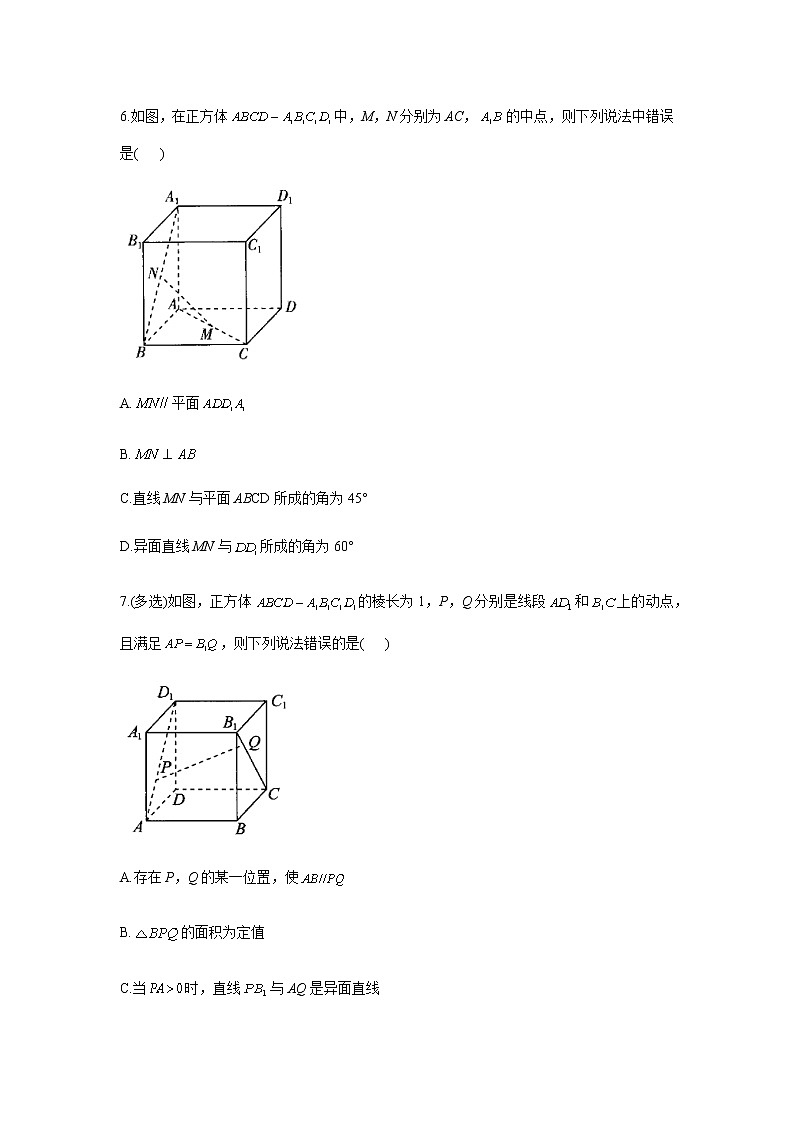
2023届新高考数学高频考点专项练习：专题十一考点30 空间点、线、面的位置关系（A卷）1.如图，在正方体中，E，F分别是，的中点，则与直线CF互为异面直线的是(   )A. B. C.DE D.AE2.下列说法正确的是(   )A.三点确定一个平面B.圆心和圆上两个点确定一个平面C.如果两个平面相交有一个交点，则必有无数个公共点D.如果两条直线没有交点，则这两条直线平行3.如图是一个正方体的平面展开图，在原正方体中，给出下列四个结论：①AB与CD垂直；②CD与EF平行；③AB与MN成60°角；④MN与EF异面.其中正确结论的序号是(   )A.①② B.①③ C.③④ D.②④4.如图，设E，F，G，H依次是空间四边形ABCD的边AB，BC，CD，DA上除端点外的点，且，，则下列结论不正确的是(   )A.当时，四边形EFGH是平行四边形B.当时，四边形EFGH是梯形C.当时，四边形EFGH是平行四边形D.当时，四边形EFGH是梯形5.设a，b是两条不同的直线，是三个不同的平面，则下列结论正确的是(   )A.若，则B.若，则且C.若，则D.若，则6.如图，在正方体中，M，N分别为AC，的中点，则下列说法中错误是(   )A.平面B.C.直线MN与平面ABCD所成的角为45°D.异面直线MN与所成的角为60°7.(多选)如图，正方体的棱长为1，P，Q分别是线段和上的动点，且满足，则下列说法错误的是(   )A.存在P，Q的某一位置，使B.的面积为定值C.当时，直线与AQ是异面直线D.无论P，Q运动到任何位置，均有8.(多选)在三棱锥中，分别为的中点，平面，则下列判断中正确的是(   )A.平面  B.平面C.  D.平面平面9.(多选)如图所示，为正方体，以下四个结论中正确的有(   )A.平面B.直线与BD所成的角为60°C.二面角的正切值是D.与底面ABCD所成角的正切值是10.在正方体中，六个面内与BD成60°角的对角线共有______条.11.如图所示，G，H，M，N分别是正三棱柱的顶点或所在棱的中点，则表示直线GH，MN是异面直线的图形有__________(填序号).
 12.《九章算术》是我国的一部古代数学专著，书中记载了一种名为“刍甍”的五面体（如图），四边形ABCD为矩形，，若，和都是正三角形，且，则异面直线AE与CF所成角的大小为__________________.13.在四棱柱中，侧面都是矩形，底面四边形ABCD是菱形，且，若异面直线和所成的角是90°，则的长度是_________.14.如图所示，三棱锥中，平面，E是PC的中点.(1)求证：AE与PB是异面直线.(2)求异面直线AE与PB所成角的余弦值.15.如图，在直四棱柱中，底面ABCD是菱形，M在线段上，且.(1)求证：；(2)若四棱柱被平面MBD截得的两部分几何体体积之比为，求的值.
答案以及解析1.答案：D解析：因为直线，平面，平面，所以直线，与直线CF共面.又因为E，F分别是，的中点，所以.由平面，平面，且CF与AE不平行，可得直线CF与直线AE互为异面直线.故选D.2.答案：C解析：共线的三点不能确定一个平面，故A错误；当圆上的两个点恰为直径的端点时，不能确定一个平面，故B错误；如果两个平面相交有一个交点，则这两个平面相交于过该点的一条直线，故C正确；如果两条直线没有交点，则这两条直线平行或异面，故D错误.故选C.3.答案：C解析：画出原正方体，如图所示，连接DN，DM，由图可知①②错误；，，所以为等边三角形，所以③AB与MN成60°角是正确的；显然④MN与EF异面是正确的.4.答案：D解析：如图所示，连接BD.，，且.同理，，且..当时，，四边形EFGH是平行四边形.选项A，C正确，D错.当时，，四边形EFGH是梯形，选项B正确.5.答案：A解析：在A中，若，则，又，因此，故A正确；在B中，若，则有可能且，有可能或，故B错误；在C中，若，则或a，b相交或a，b异面，故C错误；在D中，若，则，又，则或，故D错误.故选A.6.答案：D解析：如图，连接BD，，由M，N分别为AC，的中点知.因为平面，平面，所以平面，故A正确.易知平面，平面，所以.又，所以，故B正确.易知MN与平面ABCD所成的角即为与平面ABCD所成的角，为45°，故C正确.易知MN与所成角即为与所成角，为45°，故D错误.故选D.7.答案：B解析：对于A，当P，Q分别是与的中点时，，所以A正确；对于B，当P在A处，Q在处时，的面积为，当P，Q分别是与的中点时，的面积为，故B错误；对于C，当时，若直线与AQ是共面直线，则AP与共面，与已知矛盾，故C正确；对于D，由于BC垂直于PQ在平面ABCD内的射影，所以易知，故D正确.故选B.8.答案：ABD解析：连接，因为分别为的中点，所以，以平面，故选项A正确；因为，所以.又，所以.又平面，所以.因为，所以平面，故选项B正确；因为平面，所以.又与不垂直，所以不成立，故选项C错误；因为平面平面，所以平面平面，故选项D正确，故选ABD.9.答案：AB解析：如图，连接.，，，平面.平面，.同理，.，平面，故A正确.，异面直线与BD所成的角是或其补角.是等边三角形，，故B正确.设，连接OC，则是二面角的平面角，，故C不正确.连接AC，平面ABCD，是与底面ABCD所成的角，，故D不正确.10.答案：8解析：如图，在正方体中六个面内与BD成60°角的对角线共有共8 条.11.答案：②④解析：如题干图①中，直线；题干图②中，G，H，N三点共面，但平面GHN，因此直线GH与MN异面；题干图③中，连接MG(图略)，，因此，GH与MN共面；题干图④中G，M，N三点共面，但平面GMN，所以GH与MN异面.12.答案：解析：如图，在平面ABFE中，过F作交AB于G，连接CG，则或其补角为异面直线AE与CF所成的角.设，则，.因为，，所以四边形AEFG为平行四边形，所以，，，又，所以，又，所以，所以，即异面直线AE与CF所成角的大小为.13.答案：解析：连接，由题意得四棱柱中，，所以四边形是平行四边形，所以，所以(或其补角)为和所成的角，因为异面直线和所成的角为90°，所以，因为四棱柱中，，所以，所以，所以.14.答案：(1)见解析(2)余弦值为解析：(1)假设AE与PB共面，设平面为，所以，所以平面即为平面ABE，所以平面ABE，这与平面ABE矛盾，所以AE与PB是异面直线.(2)取BC的中点F，连接EF，AF，则，所以(或其补角)就是异面直线AE与PB所成的角.因为，平面ABC，所以，，故异面直线AE与PB所成角的余弦值为.15.答案：(1)证明过程见解析.(2).解析：(1)证明：连接AC，.四边形ABCD是菱形，.是直四棱柱，平面ABCD，且平面ABCD，.又，且平面，平面，而平面，.(2)设四棱锥，底面的面积为S，高为h，则三棱锥的体积.又四棱柱的体积，四棱柱被平面MBD截得的两部分几何体体积之比，解得.