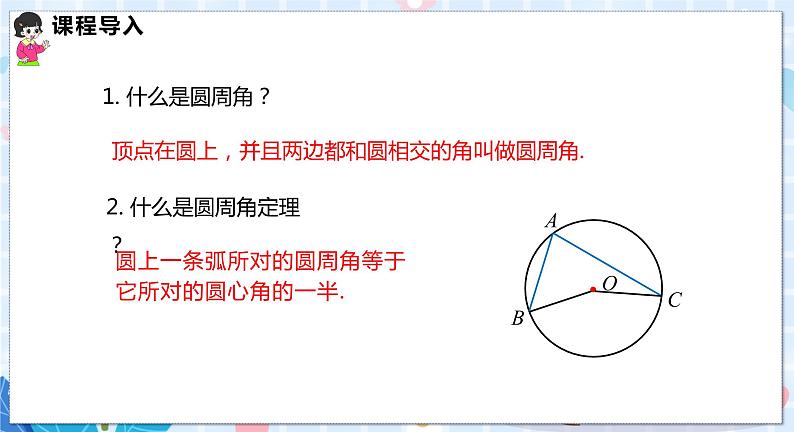
九年级下册24.3.2 圆内接四边形课文配套ppt课件

第2课时　圆内接四边形

◇教学目标◇

【知识与技能】

了解圆的内接多边形的定义,掌握圆内接四边形的性质.

【过程与方法】

1.通过观察、比较、分析,了解并证明圆内接四边形对角互补,发展学生合情推理能力和演绎推理能力;

2.通过观察图形,提高学生的识图能力;

3.通过引导学生添加合理的辅助线,培养学生的创造力.

【情感、态度与价值观】

在解决问题的过程中使学生体会到数学知识在生活中的普遍性.

◇教学重难点◇

【教学重点】

圆内接四边形对角互补的探索与运用.

【教学难点】

论证圆内接四边形对角互补.

◇教学过程◇

一、情境导入

问题:你能设法确定一个圆形纸片的圆心吗?

方法:①利用对称性,两次对折纸片找到直径的交点;

②利用“90度的圆周角所对的弦是直径”找到两条直径的交点.

练习:如图,BD是☉O的直径,∠ABC=130°,则∠ADC=　　　　°. 

二、合作探究

探究点　利用圆的内接四边形的性质进行计算或证明

典例　已知A,B,C,D是☉O上的四点,如图,延长DC,AB相交于点E,若BC=BE,求证:△ADE是等腰三角形.

[解析]　由题意可知四边形ABCD是☉O的内接四边形,∴∠A=∠BCE.

又∵BC=BE,∴∠E=∠BCE,

∴∠A=∠E,

∴DA=DE,即△ADE是等腰三角形.

圆内接四边形的角的“三种关系”:

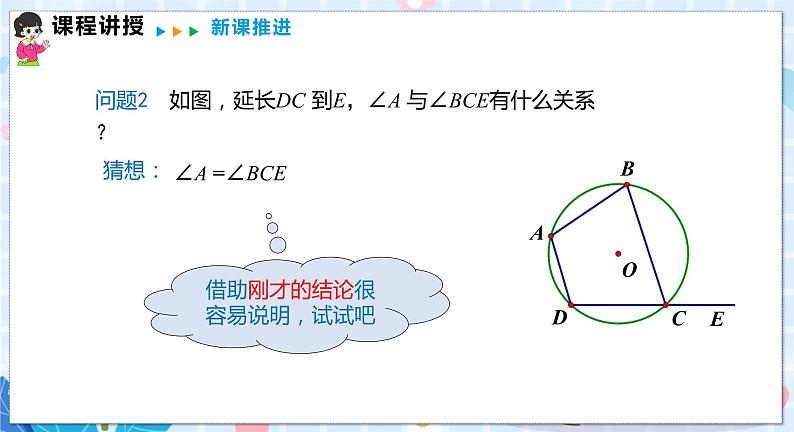
(1)对角互补;(2)四个角的和是360°;(3)圆内接四边形的外角等于它的内对角.

圆内接四边形的性质应用的常见题型:

(1)利用圆内接四边形的一组对角互补,求圆周角的度数;(2)利用圆内接四边形的外角等于它的内对角,构造相似三角形和特殊三角形,证明线段相等或乘积式成立.

变式训练　如图,☉O和☉O'都经过A,B两点,过点B作直线交☉O于点C,交☉O'于点D,G为圆外一点,GC交☉O于点E,GD交☉O'于点F.连接AE,AF.

求证:∠EAF+∠G=180°.

[解析]　如图,连接AB.

∵四边形ABCE与四边形ABDF均为圆内接四边形,

∴∠AEG=∠ABC,∠AFG=∠ABD.

又∵∠ABC+∠ABD=180°,

∴∠AEG+∠AFG=180°.

又∵四边形AEGF的内角和为360°,

∴∠EAF+∠G=180°.

三、板书设计

圆内接四边形

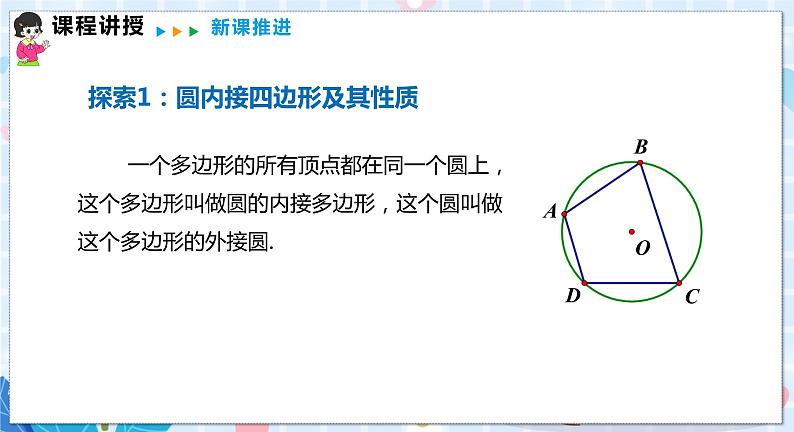
1.圆的内接多边形

2.圆的内接四边形

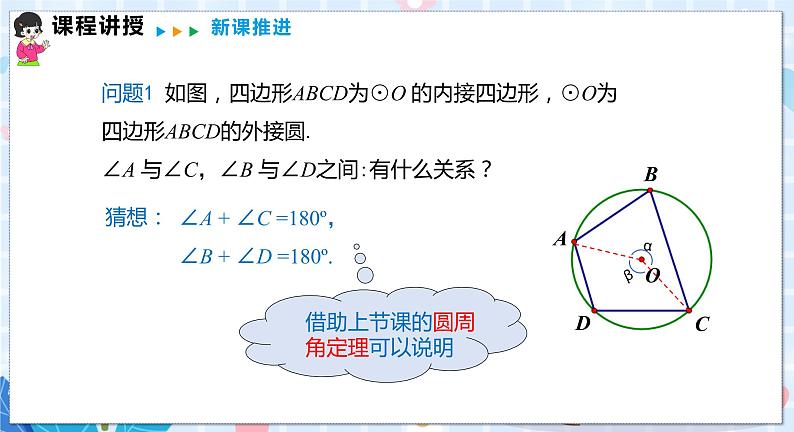
性质:圆内接四边形的对角互补.

推论:圆内接四边形的一个外角等于与它不相邻的内对角.

◇教学反思◇

本节课在原有的知识前提下,通过学生回忆、教师引导、学生再次探究,让学生自主发现问题、解决问题,培养实践能力与创新能力.