初中数学青岛版七年级下册11.1 同底数幂的乘法授课课件ppt

这是一份初中数学青岛版七年级下册11.1 同底数幂的乘法授课课件ppt，共17页。PPT课件主要包含了学习目标，复习导入，新课探究，根据乘方的意义可得，怎么计算呢，m个a，n个a，a·a··a，m+n个a，am+n等内容，欢迎下载使用。

掌握同底数幂的乘法的运算性质，能熟练地进行多个同底数幂的乘法运算；
能用符号语言和文字语言表达同底数幂乘法的运算性质；
能灵活运用同底数幂乘法的运算性质，解决简单的实际问题；
会逆用公式aman＝am＋n.
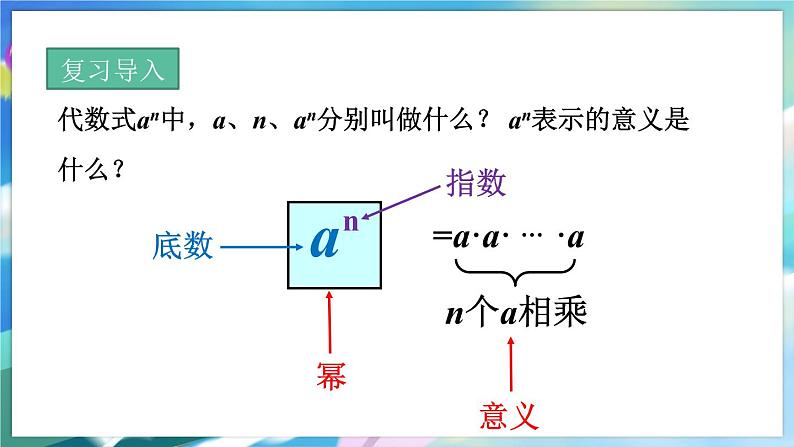
代数式an中，a、n、an分别叫做什么？ an表示的意义是什么？
少年宫的小游泳池中存有约100立方米的水.为了保证池水的清洁卫生，必须按规定的比例向池水中加施一定量的消毒剂.为此，需要将水的体积单位转换成升.100立方米的水折合成多少升呢？
102×103=（10×10）×（ 10×10×10） = 10×10× 10×10×10. =105.
这就是说，游泳池里大约有水105升.
解：1立方米=103升， 100立方米=102立方米， 100立方米=102×103升.
仿照上面的方法计算:(1)(-2)2×(-2)3 ；(2)42×45.
解：(1)(-2)2×(-2)3= [(-2)×(-2)]×[(-2)×(-2)×(-2)]=(-2)×(-2)×(-2)×(-2)×(-2)=(-2)5;
解： (2)42×45= (4×4)×(4×4×4×4×4)= 4×4×4×4×4×4×4 =47.
分别比较因数的底数与积的底数、因数的指数与积的指数，你发现了什么规律？
am·an=(a·a·…·a)· (a·a·…·a)
底数都相同，因数的指数之和等于积的指数.
同底数幂乘法的运算性质：
am·an=am+n(m，n都为正整数）
即：同底数幂相乘，底数不变，指数相加.
当m，n，p都为正整数时，你会计算吗am·an·ap吗？
根据乘方的意义， am·an·ap=(a·a·…·a)
当三个或三个以上同底数幂相乘时，同底数幂的运算性质依然成立.
【例1】计算：（1）32×35 （2）(-5)3×(-5)5
解：（1） 32×35 =32+5 =37
（2）(-5)3×(-5)5 =(-5)3+5 =(-5)8 =58
【例2】计算：（1）a8·a3·a ; （2）(a+b)2· (a+b)3
解：（1） a8·a3·a =a8+3+1 =a12
（2）(a+b)2· (a+b)3 =(a+b)2+3 =(a+b)5
把(a+b)看成整体！
注意：在同底数幂乘法中，底数可以是一个数、一个字母、一个单项式或一个多项式.
37=32×3 ，58=(-5)5×(-5)
a12=a8·a·a ，(a+b)5=(a+b)3 · (a+b)
注意：a1=a，故a不是没有指数，当指数为1时通常省略不写.
结合例1和例2，直接写出下面式子的答案，你发现了什么？
同底数幂乘法的逆运算同样成立。
同底数幂乘法的逆运算：
am+n=am·an (m，n都为正整数）
am+n+p= am·an·ap (m，n，p都为正整数）
同样地，当指数的项数大于等于3时有：
【例3】某台电脑每秒可作1015次运算，它工作5小时，可作多少次运算？
解：5×3600=5×3.6×103=1.8×10×103=1.8×104.所以，5小时=1.8×104秒. 1015×（1.8×104）=1.8×（104×1015） =1.8×1019.所以，该电脑工作5小时可作1.8×1019次的运算.
1.（1）27 × 23 （2）(-3) 4 × (-3)7
解:
(2)原式= (-3) 4+7 = (-3)11
(1)原式= 27+3
（3） (-5) 2 × (-5)3 × 54 （4）(x+y) 3× (x+y)
(3)原式= (-5) 2 × (-5)3 × (-5)4 = (-5) 2+3+4 =(-5)9 = -59
(4)原式= (x+y) 3+1 = (x+y)4
幂的底数不同时，先化为同底数幂.
2.（1）102 × 103; （2）105 × 108;（3）10m × 10n;
解：(1) 102 × 103 = 102+3 =105
(2)105 × 108 = 105+8 = 1013
(3) 10m × 10n = 10m+n
3.已知am=2，an=3，求下列各式的值：（1）am+1； （2）an+2； （3） am+n.
解：(1) am+1 = am·a =2a
(2) an+2 =an·a2 =3a2
(3) am+n =am·an =2×3 =6
分析：根据同底数幂乘法的逆运算，将所求代数式变形为同底数幂相乘的形式，再将已知整体代入即可.