





所属成套资源:2023年中考数学热点专题复习课件
2023年中考数学微专题复习课件6 最值问题模型
展开这是一份2023年中考数学微专题复习课件6 最值问题模型,共21页。PPT课件主要包含了AB=10,思路点拔,思路点拨,由已知得,△ABE≌△DAF,∠ABE=∠DAF,∠APB=90°,AB为直径的弧等内容,欢迎下载使用。
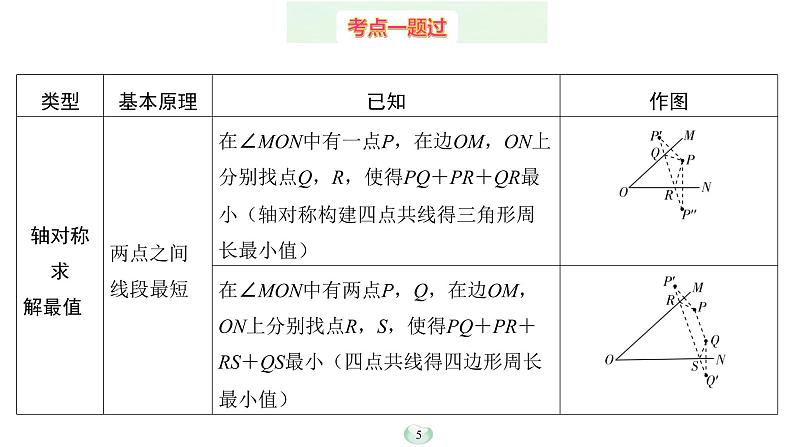
1.在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题.最值问题是全国中考的热点问题,考查形式多样化.本专题主要通过“轴对称求解最值”、“辅助圆求解最值”两个模型进行讲解.
2.解决平面几何最值问题的基本思路是共线取最值,常用的方法有:
(1)应用两点间线段最短的公理(含应用三角形的三边关系)求最值;
(2)应用垂线段最短的性质求最值;
(3)应用轴对称的性质求最值;
(4)利用点圆的判定条件和性质求最值.
▶类型1:轴对称求解最值
作点C关于直径AB的对称点E,
连接DE交AB于点F,连接CF
∠CED=30°,CE=10
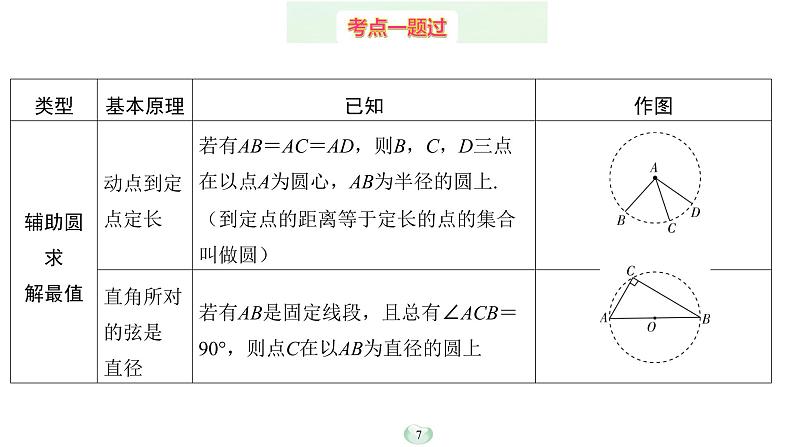
▶类型2:辅助圆求解最值
AE=DF 四边形ABCD是正方形
点P的运动轨迹是一段以
设圆心为G,连接DG交弧
于点P,此时DP为最小值
在Rt△AGD中,由勾股定理
求DG,从而求得DP的长
由翻折的性质,得由题意,得
点P的运动轨迹是一段以点E为圆心,
EC的长为半径的弧,连接AE,
交弧于点P,此时AP为最小值.
在Rt△AEF中,由勾股定理,
得AE的长,从而求得AP的长.
相关课件
这是一份中考数学复习微专题七代数最值问题模型二建立函数模型求最值课件,共9页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。
这是一份中考数学复习微专题七代数最值问题模型一运用配方法求最值课件,共6页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。
这是一份中考数学复习微专题六几何最值问题模型五线段和差——阿氏圆问题课件,共11页。PPT课件主要包含了基本模型,针对训练,针对巩固等内容,欢迎下载使用。












