中考数学三轮冲刺高分课件：专题一　 选择题突破 (含答案)

这是一份中考数学三轮冲刺高分课件：专题一　 选择题突破 (含答案)，共49页。

4. (2019苏州)苏州是全国重点旅游城市，2018年实现旅游总收入约为26 000 000万元，则数据26 000 000用科学记数法可表示为 (　　)A. 0.26×108 B. 2.6×108C. 26×106 D. 2.6×1075. (2019长沙)下列各数中，比-3小的数是 (　　)A. -5 B. -1 C. 0 D. 1
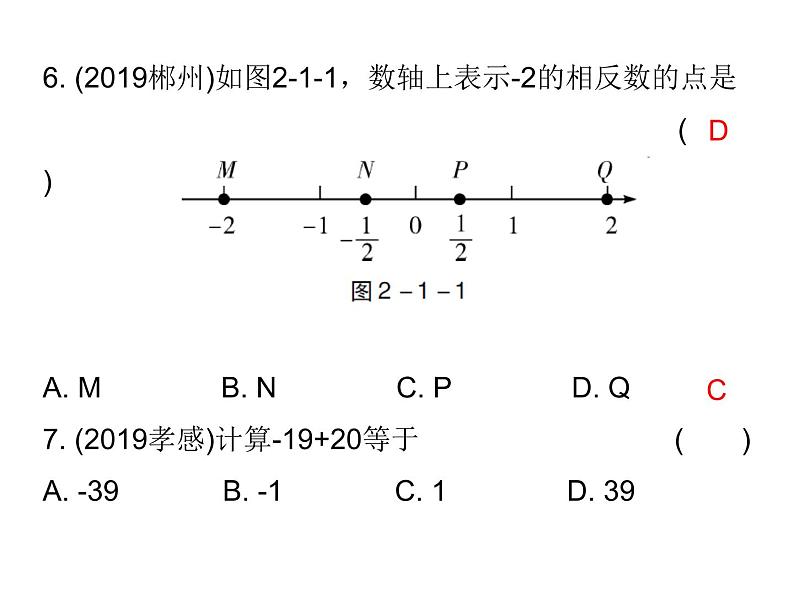
6. (2019郴州)如图2-1-1，数轴上表示-2的相反数的点是(　　)A. M B. N C. P D. Q7. (2019孝感)计算-19+20等于 (　　)A. -39 B. -1 C. 1 D. 39
8. (2019天门)下列各数中，是无理数的是 (　　)A. 3.1415 B. C. D. 9. (2019淮安)计算a·a2的结果是 (　　)A. a3 B. a2 C. 3a D. 2a210. (2019长沙)下列计算正确的是 (　　)A. 3a+2b＝5ab B. (a3)2＝a6 C. a6÷a3＝a2 D. (a+b)2＝a2+b2
23. (2019郴州)一元二次方程2x2+3x-5＝0的根的情况为 (　　)A. 有两个相等的实数根B. 有两个不相等的实数根 C. 只有一个实数根D. 没有实数根24. (2019甘肃)若一元二次方程x2-2kx+k2=0的一根为x=-1,则k的值为 (　　)A. -1 B. 0 C. 1或-1 D. 2或0
25. (2019潍坊)如图2-1-2，在矩形ABCD中，AB=2,BC=3,动点P沿折线BCD从点B开始运动到点D. 设运动的路程为x，△ADP的面积为y，那么y与x之间的函数关系的图象大致是 (　　)
26. (2019苏州)若一次函数y＝kx+b(k，b为常数,且k≠0)的图象经过点A(0，-1)，B(1，1)，则不等式kx+b＞1的解为 (　　)A. x＜0 B. x＞0 C. x＜1 D. x＞1
29. (2019重庆)抛物线y=-3x2+6x+2的对称轴是 (　　)A. 直线x=-2 B. 直线x=2C. 直线x=-1 D. 直线x=1
30. (2019烟台)已知二次函数y＝ax2+bx+c的y与x的部分对应值如下表.下列结论：①抛物线的开口向上；②抛物线的对称轴为直线x＝2；③当0＜x＜4时，y＞0；④抛物线与x轴的两个交点间的距离是4；⑤若A(x1，2)，B(x2，3)是抛物线上两点,则x1＜x2，其中正确的有 (　　)A. 2个 B. 3个 C. 4个 D. 5个
类型2 空间与图形1. (2019百色)如图2-1-4，已知a∥b，∠1＝58°，则∠2的大小是 (　　)A. 122° B. 85° C. 58° D. 322. (2019陕西)如图2-1-5，OC是∠AOB的平分线，l∥OB.若∠1＝52°，则∠2的度数为 (　　)A. 52° B. 54° C. 64° D. 69°
3. (2019玉林)若α＝29°45′，则α的余角等于 (　　)A. 60°55′ B. 60°15′ C. 150°55′ D. 150°15′ 4. (2019福建)已知正多边形的一个外角为36°，则该正多边形的边数为 (　　)A. 12 B. 10 C. 8 D. 65. (2019河北)下列图形为正多边形的是 (　　)
6. (2019徐州)下列长度的三条线段，能组成三角形的是 (　　)A. 2，2，4 B. 5，6，12C. 5，7，2 D. 6，8，107. (2019大庆)如图2-1-6，在△ABC中，BE是∠ABC的平分线，CE是外角∠ACM的平分线，BE与CE相交于点E.若∠A＝60°，则∠BEC等于 (　　)A. 15° B. 30° C. 45° D. 60°
8. (2019雅安)如图2-1-7，每个小正方形的边长均为1，则下列图形中的三角形(阴影部分)与△A1B1C1相似的是 (　　)
11. (2019河北)如图2-1-9，从点C观测点D的仰角是(　　)A. ∠DAB B. ∠DCE C. ∠DCA D. ∠ADC
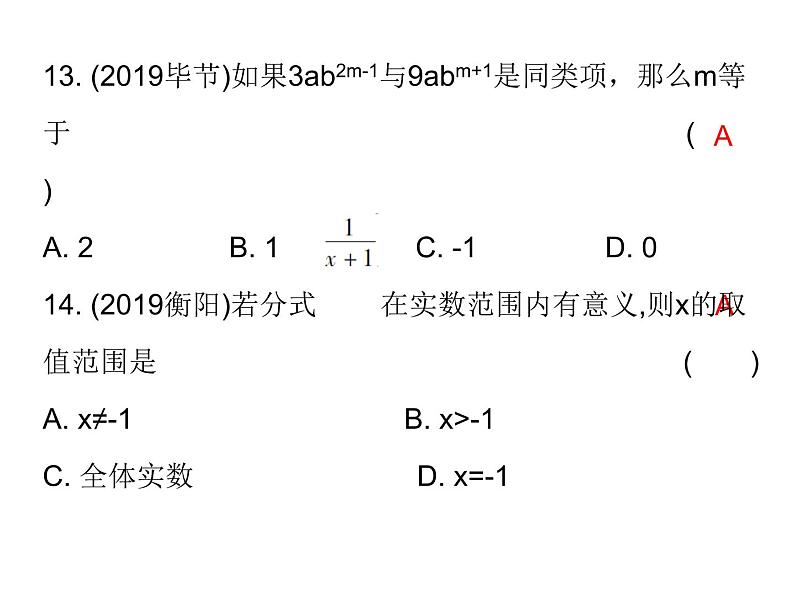
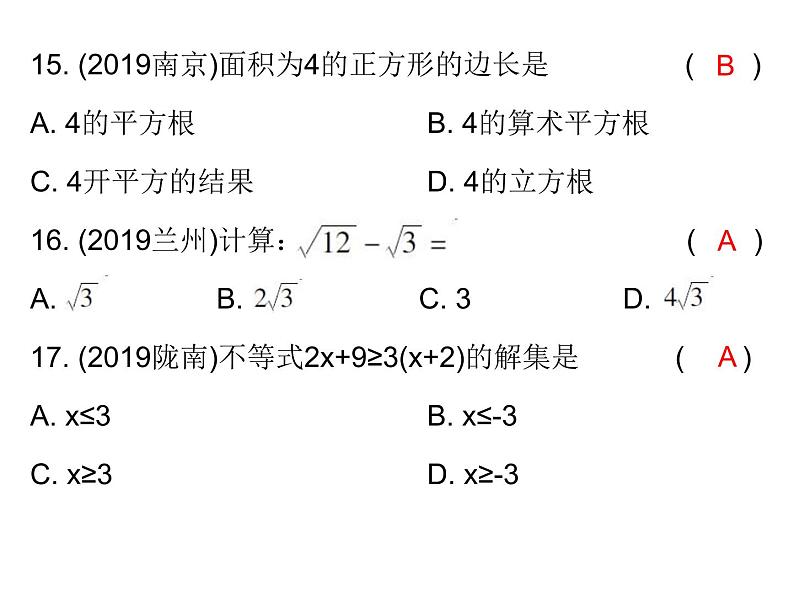
16. (2019通辽)一个菱形的边长是方程x2-8x+15＝0的一个根，其中一条对角线长为8，则该菱形的面积为 (　　)A. 48 B. 24 C. 24或40 D. 48或8017. (2019赤峰)如图2-1-13，菱形ABCD的周长为20，对角线AC，BD相交于点O，E是CD的中点，则OE的长是(　　)A. 2.5 B. 3 C. 4 D. 5
18. (2019大庆)下列说法不正确的是 (　　)A. 四边相等的四边形是菱形B. 对角线垂直的平行四边形是菱形 C. 菱形的对角线互相垂直且相等D. 菱形的邻边相等19. (2019娄底)顺次连接菱形四边中点得到的四边形是(　　)A. 平行四边形 B. 菱形C. 矩形 D. 正方形
20. (2019赤峰)如图2-1-14，AB是⊙O的弦，OC⊥AB交⊙O于点C,点D是⊙O上一点，∠ADC＝30°,则∠BOC 的度数为(　　)A. 30° B. 40° C. 50° D. 60°
23. (2019德州)如图2-1-17，点O为线段BC的中点，点A，C，D到点O的距离相等.若∠ABC=40°，则∠ADC的度数是(　　)A. 130° B. 140° C. 150° D. 160°
类型3 统计与概率1. (2018安顺)要调查安顺市中学生了解禁毒知识的情况,下列抽样调查最适合的是 (　　)A. 在某中学抽取200名女生B. 在安顺市中学生中抽取200名学生C. 在某中学抽取200名学生D. 在安顺市中学生中抽取200名男生
2. (2018内江)为了了解内江市2018年中考数学学科各分数段成绩分布情况，从中抽取400名考生的中考数学成绩进行统计分析.在这个问题中，样本是指 (　　)A. 400B. 被抽取的400名考生C. 被抽取的400名考生的中考数学成绩D. 内江市2018年中考数学成绩3. (2019连云港)一组数据3，2，4，2，5的中位数和众数分别是 (　　)A. 3，2 B. 3，3 C. 4，2 D. 4，3
4. (2019长沙)在庆祝新中国成立70周年的校园歌唱比赛中，11名参赛同学的成绩各不相同，按照成绩取前5名进入决赛. 如果小明知道了自己的比赛成绩，要判断自己能否进入决赛，小明需要知道这11名同学成绩的 (　　)A. 平均数B. 中位数 C. 众数 D. 方差5. (2019青岛)10次射击测试，他们的平均成绩相同，方差分别是s2甲=1.2，s2乙=1.1，s2丙=0.6，s2丁=0.9，则射击成绩最稳定的是 (　　)A. 甲 B. 乙 C. 丙 D. 丁
6. (2019荆州)在一次体检中，甲、乙、丙、丁四位同学的平均身高为1.65 m，而甲、乙、丙三位同学的平均身高为1.63 m，下列说法一定正确的是 (　　)A. 四位同学身高的中位数一定是其中一位同学的身高B. 丁同学的身高一定高于其他三位同学的身高 C. 丁同学的身高为1.71 mD. 四位同学身高的众数一定是1.65
7. (2019河南)某超市销售A，B，C，D四种矿泉水，它们的单价依次是5元、3元、2元、1元. 某天的销售情况如图2-1-20，则这天销售的矿泉水的平均单价是 (　　)A. 1.95元 B. 2.15元C. 2.25元 D. 2.75元
8. (2019甘肃)甲、乙两个班参加了学校组织的2019年“国学小名士”国学知识竞赛选拔赛，他们成绩的平均数、中位数、方差如下表，规定成绩大于等于95分为优异，则下列说法正确的是 (　　)A. 甲、乙两班的平均水平相同 B. 甲、乙两班竞赛成绩的众数相同 C. 甲班的成绩比乙班的成绩稳定 D. 甲班成绩优异的人数比乙班多
9. (2019福建)如图2-1-21所示是某班甲、乙、丙三位同学最近5次数学成绩及其所在班级相应平均分的折线统计图,则下列判断错误的是 (　　)A. 甲的数学成绩高于班级平均分，且成绩比较稳定B. 乙的数学成绩在班级平均分附近波动，且比丙的好C. 丙的数学成绩低于班级平均分，但成绩逐次提高D. 就甲、乙、丙三个人而言，乙的数学成绩最不稳定
10. (2019安徽)在某时段由50辆车通过一个雷达测速点，工作人员将测得的车速绘制成如图2-1-22所示的条形统计图，则这50辆车的车速的众数(单位：km/h)为 (　　)A. 60 B. 50 C. 40 D. 15
11. (2019内江)下列事件为必然事件的是 (　　)A. 袋中有4个蓝球，2个绿球，共6个球，随机摸出一个球是红球 B. 三角形的内角和为180° C. 打开电视机，任选一个频道，屏幕上正在播放广告 D. 抛掷一枚硬币两次，第一次正面向上，第二次反面向上12. (2019襄阳)下列说法错误的是 (　　)A. 必然事件发生的概率是1 B. 通过大量重复试验，可以用频率估计概率 C. 概率很小的事件不可能发生 D. 投一枚图钉，“钉尖朝上”的概率不能用列举法求得
17. (2019株洲)在一个布袋中装有红、白两种颜色的小球，它们除颜色外没有任何其他区别. 其中红球若干，白球5个，袋中的球已搅匀. 若从袋中随机取出1个球，取出红球的可能性大，则红球的个数是 (　　)A. 4个 B. 5个 C. 不足4个 D. 6个或6个以上