中考数学三轮冲刺高分课件：专题六　 解答题（二）突破 (含答案)

这是一份中考数学三轮冲刺高分课件：专题六　 解答题（二）突破 (含答案)，共55页。

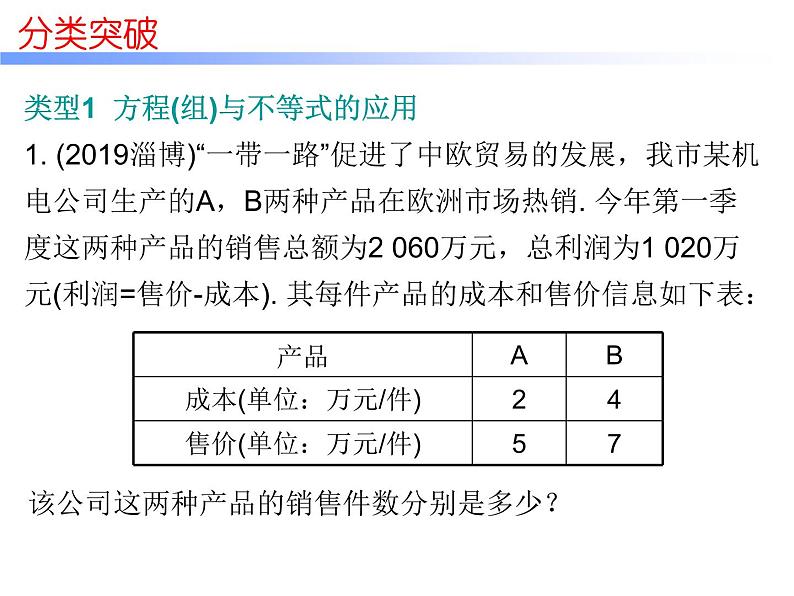
类型1 方程(组)与不等式的应用1. (2019淄博)“一带一路”促进了中欧贸易的发展，我市某机电公司生产的A，B两种产品在欧洲市场热销. 今年第一季度这两种产品的销售总额为2 060万元，总利润为1 020万元(利润=售价-成本). 其每件产品的成本和售价信息如下表：
该公司这两种产品的销售件数分别是多少？
2. (2019赤峰)某校开展校园艺术节系列活动，派小明到文体超市购买若干个文具袋作为奖品. 这种文具袋标价每个10元，请认真阅读结账时老板与小明的对话(如图2-6-1)：
(1)结合两人的对话内容,求小明原计划购买文具袋多少个;(2)学校决定，再次购买钢笔和签字笔共50支作为补充奖品，这次购买奖品总支出不超过400元. 其中钢笔标价每支8元，签字笔标价每支6元.经过沟通，这次老板给予8折优惠，那么小明最多可购买钢笔多少支？
解：(1)设小明原计划购买文具袋x个,则实际购买了(x+1)个.依题意，得10(x+1)×0.85＝10x-17. 解得x＝17. 答：小明原计划购买文具袋17个. (2)设小明可购买钢笔y支，则购买签字笔(50-y)支.依题意，得［8y+6(50-y)］×80%≤400. 解得y≤100. 即y最大值＝100. 答：小明最多可购买钢笔100支.
3. (2019宁夏)某学校在“我和我的祖国”快闪拍摄活动中,为学生化妆. 其中5名男生和3名女生共需化妆费190元；3名男生的化妆费用与2名女生的化妆费用相同. (1)求每位男生和女生的化妆费分别为多少元；(2)如果学校提供的化妆总费用为2 000元，根据活动需要至少应有42名女生化妆，那么男生中最多有多少人化妆？
4. (2019沈阳)2019年3月12日是第41个植树节.某单位积极开展植树活动，决定购买甲、乙两种树苗，用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同，每棵乙种树苗比每棵甲种树苗便宜6元. (1)求甲种树苗每棵多少元；(2)若准备用3 800元购买甲、乙两种树苗共100棵，则至少要购买乙种树苗多少棵？
5. (2019玉林)某养殖场为了响应党中央的扶贫政策，今年起采用“场内+农户”养殖模式，同时加强对蛋鸡的科学管理，蛋鸡的产蛋率不断提高，三月份和五月份的产蛋量分别是2.5万千克与3.6万千克，现假定该养殖场蛋鸡产蛋量的月增长率相同. (1)求该养殖场蛋鸡产蛋量的月平均增长率；(2)假定当月产的鸡蛋当月在各销售点全部销售出去，且每个销售点每月平均销售量最多为0.32万千克. 如果要完成六月份的鸡蛋销售任务，那么该养殖场需在五月份已有的销售点的基础上至少再增加多少个销售点？
6. (2018贵阳)某青春党支部在精准扶贫活动中，给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种. 已知乙种树苗的价格比甲种树苗贵10元，用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同. (1)求甲、乙两种树苗每棵的价格各是多少元；(2)在实际帮扶中，他们决定再次购买甲、乙两种树苗共50棵.此时，甲种树苗的售价比第一次购买时降低了10%，乙种树苗的售价不变.如果再次购买两种树苗的总费用不超过1 500元，那么他们最多可购买多少棵乙种树苗？
类型2 解直角三角形的应用1. (2019怀化)如图2-6-2，为测量一段笔直自西向东的河流的河面宽度，小明在南岸B处测得对岸A处一棵柳树位于北偏东60°方向.他以每秒1.5 m的速度沿着河岸向东步行40秒后到达C处，此时测得柳树位于北偏东30°方向，试计算此段河面的宽度.
解：如答图2-6-1，作AD⊥BC于点D.由题意可知BC=1.5×40=60(m),∠ABD=30°,∠ACD=60°.
2. (2019海南)如图2-6-3所示是某区域的平面示意图，码头A在观测站B的正东方向，码头A的北偏西60°方向上有一小岛C，小岛C在观测站B的北偏西15°方向上，码头A到小岛C的距离AC为10海里. (1)填空：∠BAC＝______度，∠C＝______度；(2)求观测站B到AC的距离BP.(结果保留根号)
4. (2018黄冈)如图2-6-5，在大楼AB正前方有一斜坡CD，坡角∠DCE=30°，楼高AB=60 m，在斜坡下的点C处测得楼顶B的仰角为60°，在斜坡上的D处测得楼顶B的仰角为45°，其中点A，C，E在同一直线上. (1)求坡底C点到大楼的距离AC的值；(2)求斜坡CD的长度.
类型3 统计图表综合题1. (2019衡阳)某学校为了丰富学生课余生活，开展了“第二课堂”的活动，推出了以下四种选修课程：A. 绘画；B. 唱歌；C. 演讲；D. 十字绣.学校规定：每个学生都必须报名且只能选择其中的一个课程.学校随机抽查了部分学生，对他们选择的课程情况进行了统计，并绘制成如图2-6-6所示两幅不完整的统计图. 请结合统计图中的信息解决下列问题：
(1)这次学校抽查的学生人数是______人；(2)将条形统计图补充完整；(3)如果该校共有1 000名学生，请你估计该校报D课程的学生约有多少人.
解：(2)选择C课程的人数为40-12-14-4=10(人)，补充条形统计图如答图2-6-4.
2. (2019长沙)某学校开展了主题为“垃圾分类，绿色生活新时尚”的宣传活动. 为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查，将他们的得分按优秀、良好、合格、待合格四个等级进行统计，并绘制了如下不完整的统计表和条形统计图(如图2-6-7).
(1)本次调查随机抽取了______名学生；表中m＝______,n＝______；(2)补全条形统计图；(3)若全校有2 000名学生，请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
3. (2019河南)某校为了解七、八年级学生对“防溺水”安全知识的掌握情况，从七、八年级各随机抽取50名学生进行测试，并对成绩(百分制)进行整理、描述和分析. 部分信息如下：a. 七年级学生成绩频数分布直方图(如图2-6-8)：
b. 七年级学生成绩在70≤x＜80这一组的如下：70 72 74 75 76 76 77 77 77 78 79c. 七、八年级学生成绩的平均数、中位数如下：
根据以上信息，回答下列问题：(1)在这次测试中，七年级在80分以上(含80分)的有_____人；(2)表中m的值为______；
(3)在这次测试中，七年级学生甲与八年级学生乙的成绩都是78分，请判断两位学生在各自年级的排名谁更靠前，并说明理由；(4)该校七年级学生有400人，假设全部参加此次测试，请估计七年级成绩超过平均数76.9分的人数.
4. (2019天门)为了解某地七年级学生身高情况，随机抽取部分学生，测得他们的身高(单位： cm)，并绘制了如图2-6-9所示两幅不完整的统计图.请结合图中提供的信息，解答下列问题. (1)填空：样本容量为______，a＝______；(2)把频数分布直方图补充完整；(3)若从该地随机抽取1名学生，估计这名学生身高低于160 cm的概率.
解：(2)补全频数分布直方图如答图2-6-6.
类型4 求事件的概率1. (2019苏州)在一个不透明的盒子中装有4张卡片，4张卡片的正面分别标有数字1，2，3，4，这些卡片除数字外都相同，将卡片搅匀. (1)从盒子中任意抽取一张卡片，恰好抽到标有奇数卡片的概率是______；(2)先从盒子中任意抽取一张卡片，再从余下的3张卡片中任意抽取一张卡片，求抽取的2张卡片标有数字之和大于4的概率. (请用画树状图或列表法求解)
解：(2)根据题意列表，得
2. (2019南京)某校计划在暑假第二周的星期一至星期四开展社会实践活动，要求每位学生选择两天参加活动. (1)甲同学随机选择两天,其中有一天是星期二的概率是多少?(2)乙同学随机选择连续的两天，其中有一天是星期二的概率是______.
3. (2019淮安)在三张大小、质地均相同的卡片上各写一个数字，分别为5,8,8.现将三张卡片放入一只不透明的盒子中，搅匀后从中任意摸出一张，记下数字后放回，搅匀后再任意摸出一张，记下数字. (1)用树状图或列表的方法列出所有可能结果；(2)求两次摸到不同数字的概率.
4. (2019黄石)将正面分别写着数字1，2，3的三张卡片(注：这三张卡片的形状、大小、质地、颜色等其他方面完全相同，若背面朝上放在桌面上，这三张卡片看上去无任何差别)洗匀后，背面朝上放在桌面上.甲从中随机抽取一张卡片，记该卡片上的数字为m，然后放回洗匀，背面朝上放在桌面上，再由乙从中随机抽取一张卡片，记该卡片上的数字为n，组成一数对(m，n). (1)请写出(m，n)所有可能出现的结果；(2)甲、乙两人玩游戏，规则如下：按上述要求，两人各抽一次卡片，卡片上数字之和为奇数则甲赢，数字之和为偶数则乙赢. 你认为这个游戏公平吗？请说明理由.
类型5 三角形的计算与证明1. (2019温州)如图2-6-10，在△ABC中，AD是BC边上的中线，E是AB边上一点,过点C作CF∥AB交ED的延长线于点F. (1)求证：△BDE≌△CDF;(2)当AD⊥BC，AE=1，CF=2时，求AC的长.
(1)证明：∵CF∥AB，∴∠B=∠FCD，∠BED=∠F.∵AD是BC边上的中线，∴BD=CD.∴△BDE≌△CDF(AAS).(2)解：∵△BDE≌△CDF，∴BE=CF=2.∴AB=AE+BE=1+2=3.∵AD⊥BC，BD=CD，∴AC=AB=3.
2. 如图2-6-11，△ABC为等边三角形，过点B作BD⊥AC于点D，过点D作DE∥BC，且DE=CD，连接CE.(1)求证：△CDE为等边三角形；(2)连接BE，若AB=4，求BE的长.
3. (2017苏州)如图2-6-12，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O. (1)求证：△AEC≌△BED；(2)若∠1=42°，求∠BDE的度数.
4. (2019临沂)如图2-6-13，在△ABC中，∠ACB＝120°, BC＝4，D为AB的中点，DC⊥BC，求△ABC的面积.
解：∵DC⊥BC，∴∠BCD＝90°.∵∠ACB＝120°，∴∠ACD＝30°.延长CD到点H使DH＝CD，连接AH，如答图2-6-10.
类型6 四边形的计算与证明1. (2019本溪)如图2-6-14，在四边形ABCD中，AB∥CD，AD⊥CD，∠B＝45°，延长CD到点E，使DE＝DA，连接AE. (1)求证：AE＝BC；(2)若AB＝3，CD＝1，求四边形ABCE的面积.
(1)证明：∵AB∥CD，∠B＝45°，∴∠C+∠B＝180.∴∠C＝135°.∵DE＝DA，AD⊥CD,∴∠E＝45°.∴∠E+∠C＝180°. ∴AE∥BC.又∵AB∥CD，∴四边形ABCE是平行四边形.∴AE＝BC.(2)解：∵四边形ABCE是平行四边形，∴AB＝CE＝3.∴AD＝DE＝AB-CD＝2.∴四边形ABCE的面积＝3×2＝6.
2. (2019鄂州)如图2-6-15，矩形ABCD中，AB＝8，AD＝6，点O是对角线BD的中点，过点O的直线分别交AB，CD边于点E，F. (1)求证：四边形DEBF是平行四边形；(2)当DE＝DF时，求EF的长.
(1)证明：∵四边形ABCD是矩形，∴AB∥CD.∴∠DFO＝∠BEO.又∵∠DOF＝∠BOE，OD＝OB，∴△DOF≌△BOE(AAS).∴DF＝BE.又∵DF∥BE，∴四边形BEDF是平行四边形.(2)解：∵DE＝DF，四边形BEDF是平行四边形,∴四边形BEDF是菱形.∴DE＝BE，EF⊥BD，OE＝OF.设AE＝x，则DE＝BE＝8-x.
3. (2019连云港)如图2-6-16，在△ABC中，AB=AC. 将△ABC沿着BC方向平移得到△DEF，其中点E在边BC上，DE与AC相交于点O. (1)求证：△OEC为等腰三角形；(2)连接AE,DC,AD，当点E在什么位置时，四边形AECD为矩形?并说明理由.
(1)证明：∵AB=AC，∴∠B=∠ACB.∵△ABC平移得到△DEF，∴AB∥DE.∴∠B=∠DEC. ∴∠ACB=∠DEC，∴OE=OC，即△OEC为等腰三角形.(2)解：当E为BC的中点时，四边形AECD是矩形.理由如下.∵AB=AC，E为BC的中点，∴AE⊥BC，BE=EC.∵△ABC平移得到△DEF，∴BE∥AD，BE=AD.∴AD∥EC，AD=EC.∴四边形AECD是平行四边形.∵AE⊥BC，∴四边形AECD是矩形.
(1)证明：连接BD，BD与AC相交于点O，如答图2-6-11.∵四边形ABCD是菱形，∴AB＝AD，AC⊥BD,OB＝OD.∵BE＝DF，∴AB∶BE＝AD∶DF.∴EF∥BD. ∴AC⊥EF.
5. (2019内江)如图2-6-18，在正方形ABCD中，点E是BC上的一点，点F是CD延长线上的一点，且BE＝DF，连接AE,AF,EF. (1)求证：△ABE≌△ADF；(2)若AE＝5，请求出EF的长.
6. (2019潍坊)如图2-6-19，正方形ABCD的边CD在正方形ECGF的边CE上，连接DG，过点A作AH∥DG，交BG于点H. 连接HF，AF，其中AF交EC于点M. (1)求证：△AHF为等腰直角三角形;(2)若AB=3，EC=5，求EM的长.
(1)证明：∵四边形ABCD，四边形ECGF都是正方形，∴DA∥BC，AD=CD，FG=CG，∠B=∠CGF=90°.∵AD∥BC，AH∥DG，∴四边形AHGD是平行四边形.∴AH=DG，AD=HG=CD.∵CD=HG，∠DCG=∠HGF=90°，CG=GF，∴△DCG≌△HGF(SAS).∴DG=HF，∠HFG=∠HGD.∴AH=HF. ∵∠HGD+∠DGF=90°，∴∠HFG+∠DGF=90°. ∴DG⊥HF.