中考数学三轮冲刺高分课件：专题七　 解答题（三）突破 (含答案)

这是一份中考数学三轮冲刺高分课件：专题七　 解答题（三）突破 (含答案)，共54页。

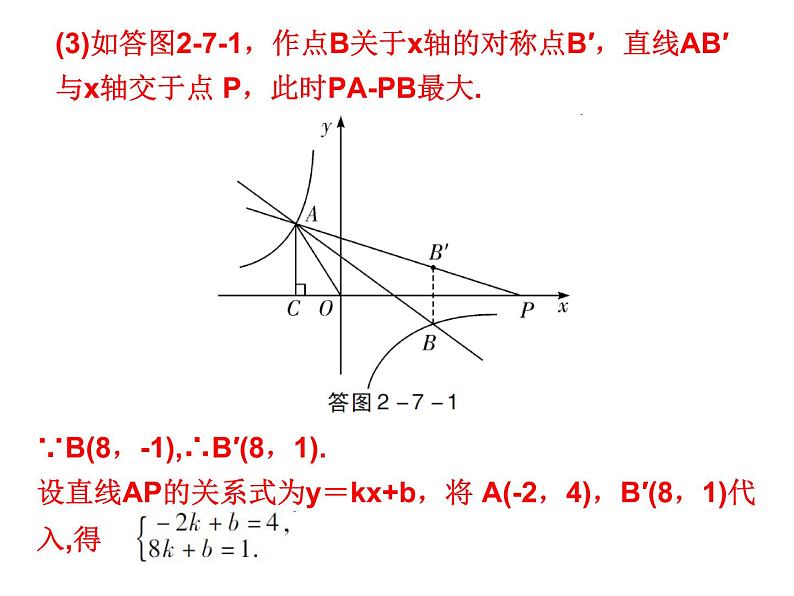
(3)如答图2-7-1，作点B关于x轴的对称点B′，直线AB′与x轴交于点 P，此时PA-PB最大.
①求出一个满足以上条件的点P的横坐标；②直接回答:这样的点P共有几个？
2. (2019深圳)如图2-7-6,抛物线y=ax2+bx+c过点A(-1,0),点C(0,3)，且OB=OC. (1)求抛物线的解析式及其对称轴；(2)如图2-7-6①，点D，E是在直线x=1上的两个动点，且DE=1，点D在点E的上方,求四边形ACDE的周长的最小值. (3)如图2-7-6②，点P为抛物线上一点，连接CP，若直线CP把四边形CBPA的面积分为3∶5两部分，求点P的坐标.
3. (2019吉林)如图2-7-7，抛物线y＝(x-1)2+k与x轴相交于A，B两点(点A在点B的左侧)，与y轴相交于点C(0，-3). P为抛物线上一点，横坐标为m，且m＞0. (1)求此抛物线的解析式；(2)当点P位于x轴下方时，求△ABP面积的最大值；(3)设此抛物线在点C与点P之间部分(含点C和点P)最高点与最低点的纵坐标之差为h. ①求h关于m的函数解析式，并写出自变量m的取值范围；②当h＝9时，直接写出△BCP的面积.
类型3 圆的综合题1. (2019广东)如图2-7-9①，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，过点C作∠BCD＝∠ACB交⊙O于点D，连接AD交BC于点E，延长DC至点F，使CF＝AC，连接AF. (1)求证：ED＝EC；(2)求证：AF是⊙O的切线；(3)如图2-7-9②，若点G是△ACD的内心，BC·BE＝25，求BG的长.
2. (2018广东)如图2-7-10，四边形ABCD中，AB=AD=CD，以AB为直径的⊙O经过点C，连接AC，OD交于点E. (1)求证：OD∥BC；(2)若tan∠ABC=2，求证：DA与⊙O相切；(3)在(2)条件下，连接BD交⊙O于点F，连接EF.若BC=1，求EF的长.
(1)证明：∵FP是⊙O的切线，∴∠OCP=90°.∵AF⊥PC，∴∠F=90°. ∴∠F=∠OCP.∴AF∥OC.∴∠FAC=∠ACO.∵OA=OC,∴∠ACO=∠CAO. ∴∠FAC=∠CAO. ∴AC平分∠FAB.(2)证明：∵OC=OB，∴∠OCB=∠OBC.∵PF是⊙O的切线，CE⊥AB，∴∠OCP=∠CEB=90°.∴∠PCB+∠OCB=90°，∠BCE+∠OBC=90°.∴∠BCE=∠BCP.∵CD是直径，∴∠CBD=∠CBP=90°，∴△CBE∽△CPB.
(1)证明：∵∠DBC=∠DAC，∠ACH=∠CBD，∴∠DAC=∠ACH. ∴AD∥CH.又∵AD=CH,∴四边形ADCH是平行四边形.(2)①证明：∵AB是直径，∴∠ACB=90°=∠ADB.又∵AC=BC，∴∠CAB=∠ABC=45°，∴∠CDB=∠CAB=45°.∵AD∥CH，∴∠ADH=∠CHD=90°.又∵∠CDB=45°，∴∠CDB=∠DCH=45°.∴CH=DH. ∴△DHC为等腰直角三角形.②解：∵四边形ABCD是⊙O的圆内接四边形，∴∠ADP=∠PBC.又∵∠P=∠P，∴△ADP∽△CBP.
(2)证明：连接AE，如答图2-7-7.∵PA为⊙O的切线，∴∠PAE+∠OAE＝90°.∵AD⊥ED，∴∠EAD+∠AED＝90°.∵OE＝OA，∴∠OAE＝∠AED.∴∠PAE＝∠DAE，即EA平分∠PAD.∵PA,PB为⊙O的切线，∴PD平分∠APB.∴点E为△PAB的内心.