小学数学冀教版五年级上册三角形面积试讲课ppt课件

这是一份小学数学冀教版五年级上册三角形面积试讲课ppt课件，共24页。PPT课件主要包含了Sah，完全一样，三角形纸片，直角三角形，锐角三角形，钝角三角形，一起动手试一试，长方形，平行四边形，拼成平行四边形的底等内容，欢迎下载使用。

求下面平行四边形的面积。
6×10 = 60（cm2）
回忆一下，生活中我们在哪些地方见过三角形？
你还能说出那些物体上有三角形吗？
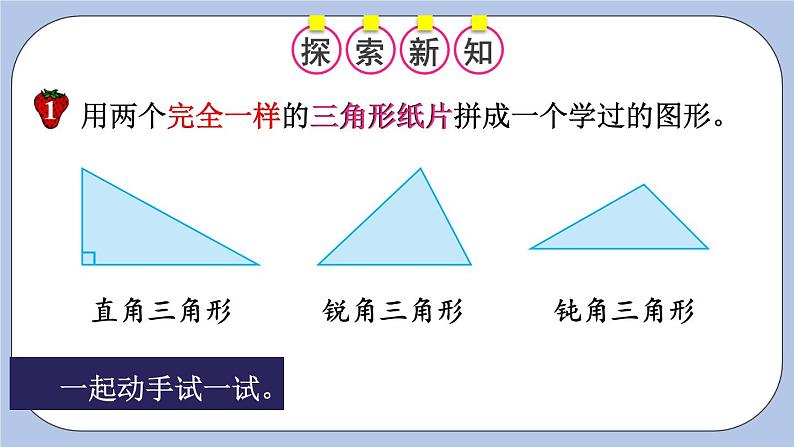
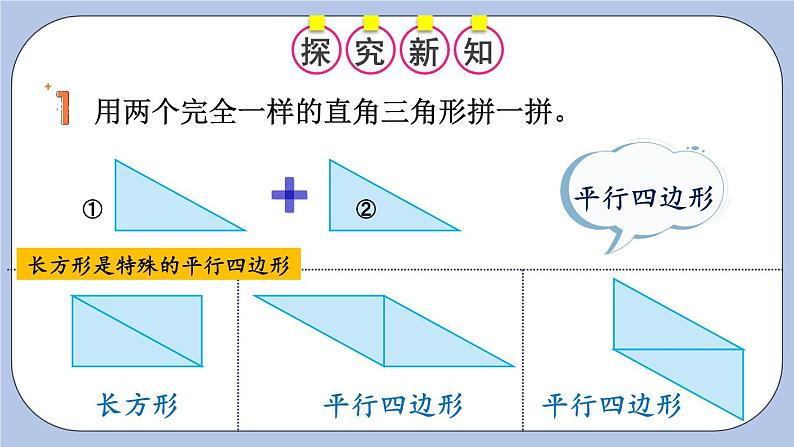
用两个完全一样的直角三角形拼一拼。
长方形是特殊的平行四边形
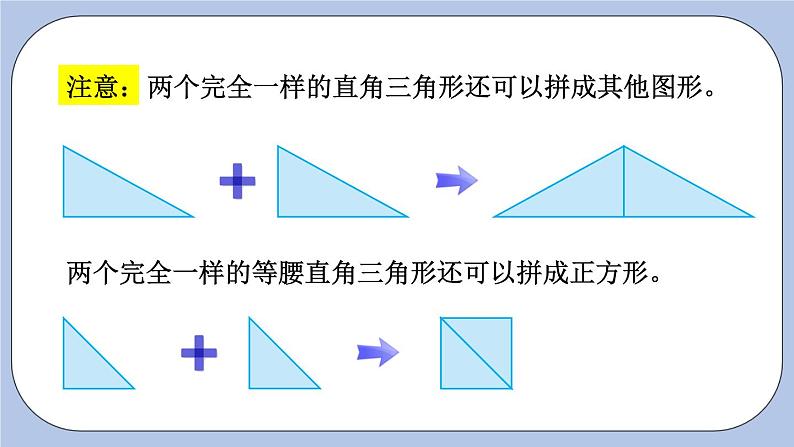
两个完全一样的直角三角形还可以拼成其他图形。
两个完全一样的等腰直角三角形还可以拼成正方形。
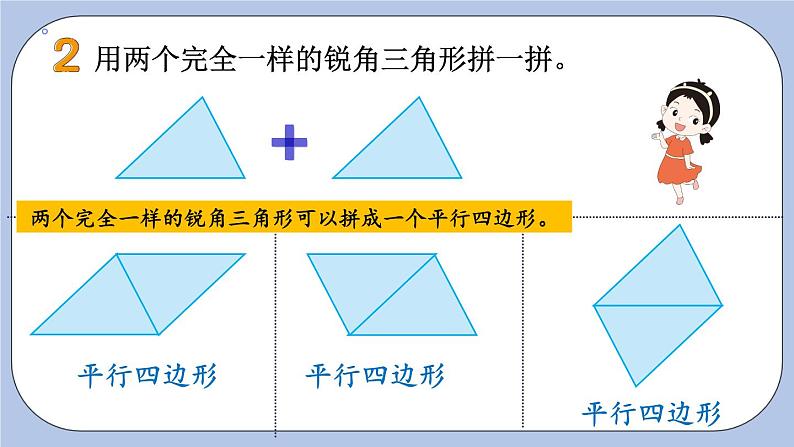
用两个完全一样的锐角三角形拼一拼。
两个完全一样的锐角三角形可以拼成一个平行四边形。
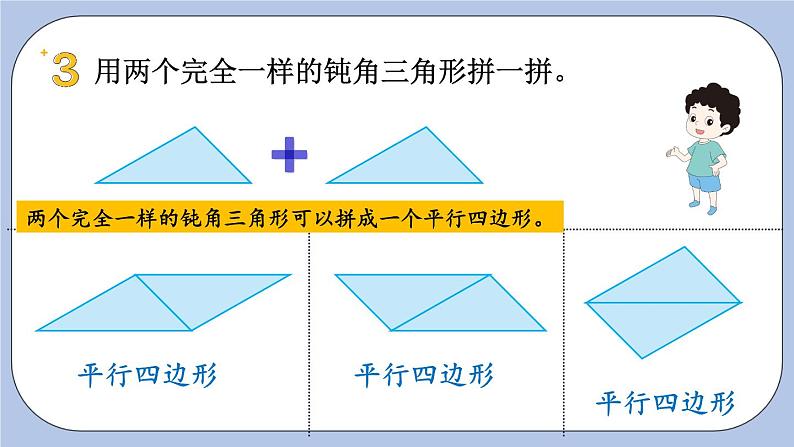
用两个完全一样的钝角三角形拼一拼。
两个完全一样的钝角三角形可以拼成一个平行四边形。
任意两个完全一样的三角形都可以拼成一个平行四边形。
小组合作，讨论下面的问题。（1）拼成的平行四边形的底和高与三角 形的底和高有什么关系？（2）三角形的面积和平行四边形的面积 有什么关系？（3）怎样计算三角形的面积？
（1）拼成的平行四边形的底和高与三角形的底和高有什么关系？
（2）三角形的面积和平行四边形的面积有什么关系？
拼成的平行四边形的面积 =_____________________
平行四边形的面积 = 底 × 高
（3）怎样计算三角形的面积？
如果用S表示三角形的面积，三角形面积的计算公式可以写成:
除了上面的拼接法我们还可以怎样来推导三角形的面积公式？
拼成的平行四边形的面积=三角形的底×(三角形的高÷2)
折叠后的长方形的面积 =(三角形的底÷2)×(三角形的高÷2)
《九章算术》是我国古代最重要的数学专著，分为九章。第一章“方田”记载了长方形、三角形、梯形等土地面积的计算方法。例如，三角形的面积是“半广以乘正从（读zòng）”，其中“广”和“正从”是指三角形的底和高。 我国古代伟大的数学家刘徽，在公元263年完成了对《九章算术》的注解、整理工作。他在注解中，应用割补（古代称“以盈补虚”）的方法，证明了三角形的面积公式。
计算下面三角形的面积。
8×3÷2 = 12（平方厘米）
14×20÷2 = 140（平方厘米）
1.8×0.6÷2 = 0.54（平方厘米）
1.计算下面每个图形的面积。
【选自教材P59页 练一练 第2题】
21×13÷2 = 136.5（平方厘米）
1.6×1.6÷2 = 1.28（平方厘米）
9×10.5= 94.5（平方米）
2.计算下面每个三角形的面积。（1）底是9分米，高是5.2分米。（2）底是1.5米，高是1.2米。
【选自教材P59页 练一练 第3题】
9×5.2÷2 = 23.4（平方分米）
1.5×1.2÷2 = 0.9（平方米）
3.有一张三角形的三合板，它的底是1.4米，高是1.2米。 这张三合板的面积是多少平方米?
【选自教材P59页 练一练 第4题】
1.4×1.2÷2 = 0.84（平方米）
答：这张三合板的面积是0.84平方米。
4.在下面的两条平行线间分别画一个三角形和一个平行 四边形，使它们的面积都与已知三角形的面积相等。