北京课改版七年级上册第三章 简单的几何图形3.9 两条直线的位置关系评优课ppt课件

这是一份北京课改版七年级上册第三章 简单的几何图形3.9 两条直线的位置关系评优课ppt课件，共28页。PPT课件主要包含了举一反三，°39′，新知3垂直等内容，欢迎下载使用。

(1) 在同一平面内，两条直线的位置关系有相交和平行两种. 若两条直线只有一个公共点，我们称这两条直线为相交线；在同一平面内，不相交的两条直线叫做平行线.
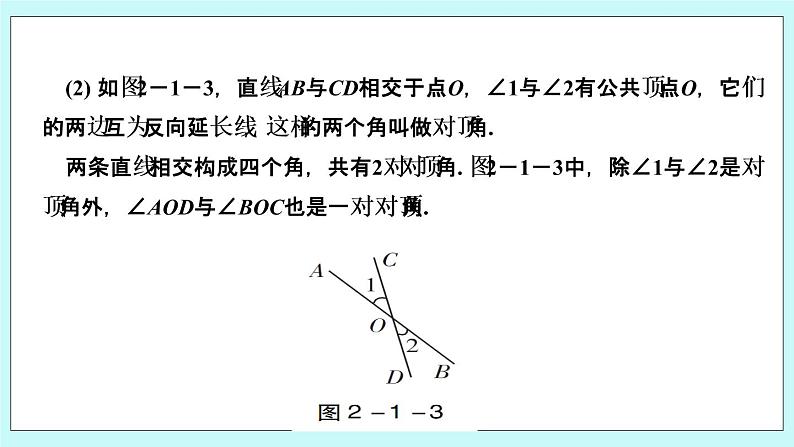
(2) 如图2－1－3，直线AB与CD相交于点O，∠1与∠2有公共顶点O，它们的两边互为反向延长线，这样的两个角叫做对顶角.两条直线相交构成四个角，共有2对对顶角. 图2－1－3中，除∠1与∠2是对顶角外，∠AOD与∠BOC也是一对对顶角.
(3) 对顶角的性质：对顶角相等.
找一个角的对顶角可以反向延长这个角的两边，以延长线为边的角即是原角的对顶角，对顶角是成对出现的.
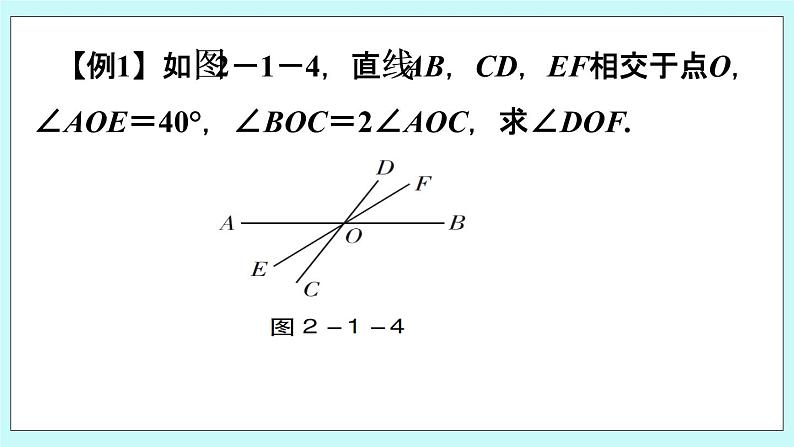
【例1】如图2－1－4，直线AB，CD，EF相交于点O，∠AOE＝40°，∠BOC＝2∠AOC，求∠DOF.
解析 图形中∠BOC与∠AOC互为邻补角，结合已知条件∠BOC＝2∠AOC，则可求出∠AOC，要求∠DOF只需求它的对顶角∠EOC即可，本题可用方程求解.解 设∠AOC＝x°，则∠BOC＝(2x)°.因为∠AOC＋∠BOC＝180°，所以x＋2x＝180，解得x＝60. 所以∠AOC＝60°. 因为∠DOF与∠EOC是对顶角，所以∠DOF＝∠EOC＝∠AOC－∠AOE ＝60°－40°＝20°.
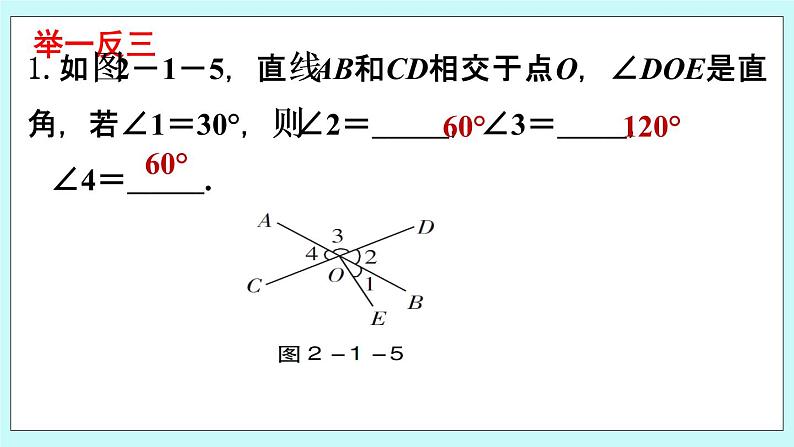
如图2－1－5，直线AB和CD相交于点O，∠DOE是直角，若∠1＝30°，则∠2＝ ，∠3＝ ，∠4＝ .
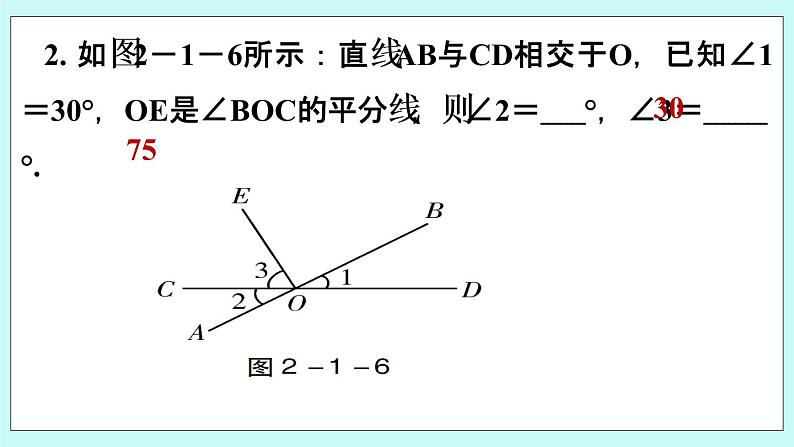
2. 如图2－1－6所示：直线AB与CD相交于O，已知∠1＝30°，OE是∠BOC的平分线，则∠2＝ °，∠3＝ °.
3. 如图2－1－7，直线AB，CD相交于点O，EO⊥AB，垂足为O. 若∠EOD＝35°，则∠AOC的度数为 .
新知2 余角、补角的概念和性质
(1)余角和补角的概念.①如果两个角的和是90°，那么称这两个角互为余角；②如果两个角的和是180°，那么称这两个角互为补角.(2)性质：同角或等角的余角相等，同角或等角的补角相等.①同角或等角的余角相等包含两方面内容：一是同一个角的余角相等；二是相等的角的余角相等；②同角或等角的补角相等也是这样理解的.
【例2】已知∠α＝50°17′，求∠α的余角和补角.解析 根据余角、补角的定义求解.解 ∠α的余角为90°－50°17′＝39°43′， ∠α的补角为180°－50°17′＝129°43′.
1. 一个角是50°21′，则它的余角是 ；补角是 .2. 一个角的补角是它的3倍，则这个角的度数是 .3. 如图2－1－8，∠AOC和∠DOB都是直角，如果∠DOC＝26°，那么∠AOB的度数是 .
(1)两条直线相交所成的四个角，如果有一个角是直角，那么称这两条直线互相垂直，其中的一条直线叫做另一条直线的垂线，它们的交点叫做垂足.(2)平面内，过一点有且只有一条直线垂直于已知直线.(3)直线外一点与直线上各点连接的所有线段中，垂线段最短.
【例3】下面四种判定两条直线垂直的方法中，正确的有( )①两条直线相交所成的四个角中有一个角是直角，则这两条直线互相垂直；②两条直线相交，所成的四个角中，只要有两个角相等，则这两条直线互相垂直；③两条直线相交，所成的四个角相等，则这两条直线互相垂直；④两条直线相交，有一组对顶角互补，则这两条直线互相垂直.A. 4个 B. 3个 C. 2个 D. 1个
解析 此题主要考查了垂直的定义：两条直线相交成四个角，如果有一个角是直角，那么这两条之间互相垂直。直接根据垂直的定义即可判断①正确；根据对顶角的定义可以知道②不正确；两条直线相交，所成的四个角相等，则这四个角都是90°，所以③正确；根据对顶角的定义可以判定④正确. 答案 B
1. 如图2－1－9，已知直线ON⊥a，直线OM⊥a，可以推断出OM与ON重合的理由是( ) A. 两点确定一条直线B. 经过一点有且只有一条直线垂直于已知直线C. 垂线段最短D. 垂直的定义
2. 如图2－1－10，已知直线AB，CD，EF相交于点O，AB⊥CD，∠DOE＝127°，则∠COE＝ °，∠AOF＝ °.
3. 如图2－1－11，直线AB，CD相交于点O，OE⊥AB，∠COE＝68°，则∠BOD等于 .
1. (3分) 如图KT2－1－1，直线a，b相交于点O，若∠1＝40°，则∠2＝ ( )A. 140° B. 120° C. 60° D. 50°
2. (3分)如图KT2－1－2，两条直线AB，CD交于点O，射线OM是∠AOC的平分线，若∠BOD＝80°，则∠BOM等于( )A. 40° B. 120° C. 140° D. 100°
3. (3分)下列图形中∠1与∠2互为对顶角的是( )
4. (3分)如图KT2－1－3，三条直线l1，l2，l3相交于点E，则∠1＋∠2＋∠3＝( )A. 90° B. 120° C. 180° D. 360°
5. (3分)如图KT2－1－4，直线AB，CD相交于点O，EO⊥AB，垂直为点O，∠BOD＝50°，则∠COE＝( )A. 30° B. 140° C. 50° D. 60°
6. (3分)如图KT2－1－5，直线AB，CD交于点O，OA平分∠EOC，∠EOC＝70°，则∠BOD的度数是( )A. 20° B. 30° C. 35° D. 55°
7. (6分)如图KT2－1－6，直线AB，CD相交于点O，过点O作两条射线OM，ON，且∠AOM＝∠CON＝90°.
(1)若OC平分∠AOM，求∠AOD的度数；
解：(1)因为∠AOM＝∠CON＝90°，OC平分∠AOM，所以∠1＝∠AOC＝45°，所以∠AOD＝180°－∠AOC＝180°－45°＝135°；
8.(6分)如图KT2－1－7所示，已知直线AB，CD相交于点O，OE，OF为射线，∠AOE＝90°，OF平分∠AOC，∠AOF＋∠BOD＝51°，求∠EOD的度数.