中考数学总复习第09讲 多姿多彩的图形难点解析与训练

第09讲 多姿多彩的图形

考点·方法·破译

1． 会识常见的几何图形，并了解它们的名称．

2． 会画基本几何体(直棱柱、圆柱、圆锥、球)的三视图，会判断简单物体的三视图，以根据三视图描述               基本几何体或实物原型．

3． 了解基本几何体与其三视图、展开图之间的关系．

经典·考题·赏析

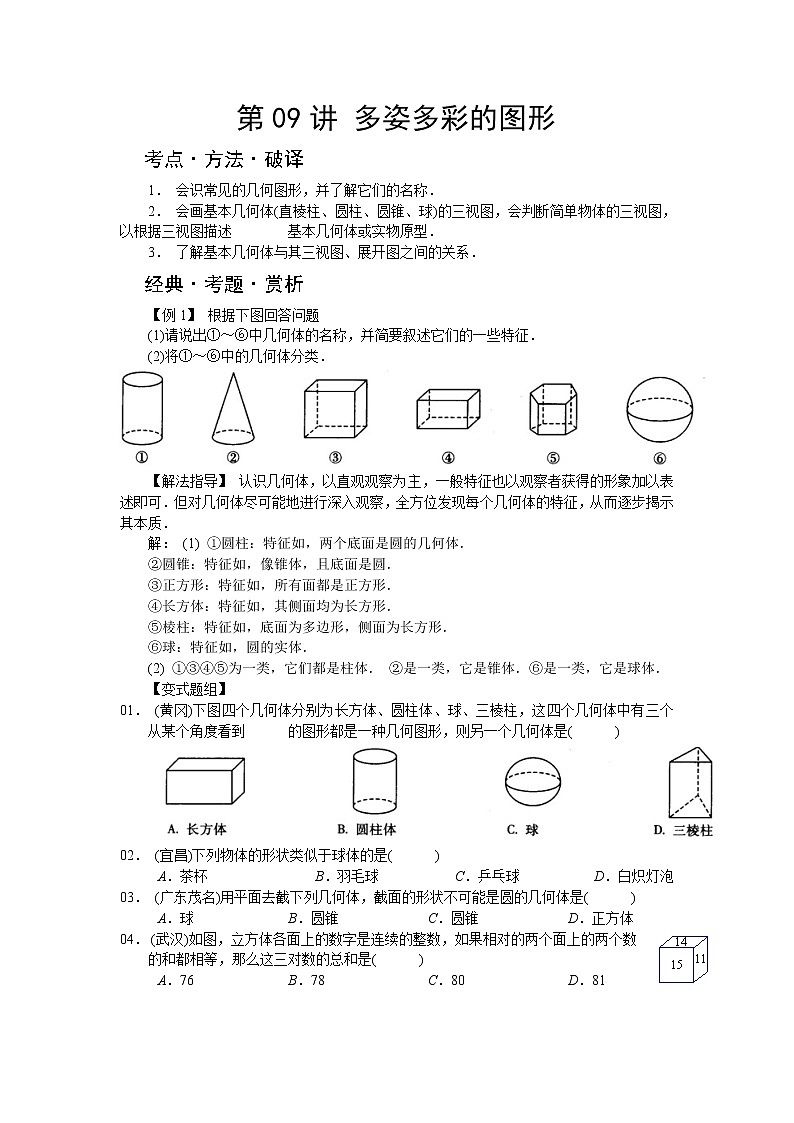
【例1】 根据下图回答问题

(1)请说出①～⑥中几何体的名称，并简要叙述它们的一些特征．

(2)将①～⑥中的几何体分类．

【解法指导】 认识几何体，以直观观察为主，一般特征也以观察者获得的形象加以表述即可．但对几何体尽可能地进行深入观察，全方位发现每个几何体的特征，从而逐步揭示其本质．

解： (1) ①圆柱：特征如，两个底面是圆的几何体．

②圆锥：特征如，像锥体，且底面是圆．

③正方形：特征如，所有面都是正方形．

④长方体：特征如，其侧面均为长方形．

⑤棱柱：特征如，底面为多边形，侧面为长方形．

⑥球：特征如，圆的实体．

(2) ①③④⑤为一类，它们都是柱体． ②是一类，它是锥体．⑥是一类，它是球体．

【变式题组】

01． (黄冈)下图四个几何体分别为长方体、圆柱体、球、三棱柱，这四个几何体中有三个从某个角度看到               的图形都是一种几何图形，则另一个几何体是(      )

02． (宜昌)下列物体的形状类似于球体的是(      )

A．茶杯    B．羽毛球   C．乒乓球   D．白炽灯泡

03． (广东茂名)用平面去截下列几何体，截面的形状不可能是圆的几何体是(      )

A．球    B．圆锥    C．圆锥    D．正方体

04． (武汉)如图，立方体各面上的数字是连续的整数，如果相对的两个面上的两个数的和都相等，那么这三对数的总和是(      )

A．76    B．78    C．80    D．81

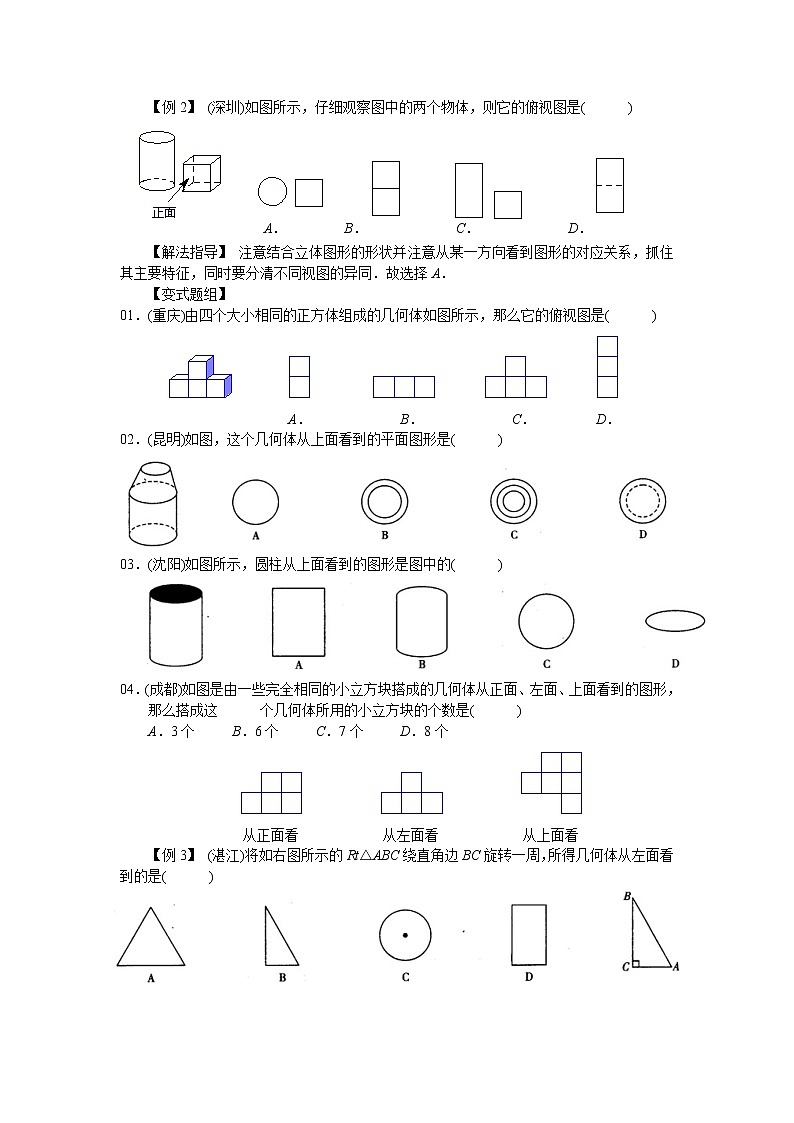
【例2】 (深圳)如图所示，仔细观察图中的两个物体，则它的俯视图是(      )

   A．   B．    C．    D．

【解法指导】 注意结合立体图形的形状并注意从某一方向看到图形的对应关系，抓住其主要特征，同时要分清不同视图的异同．故选择A．

【变式题组】

01．(重庆)由四个大小相同的正方体组成的几何体如图所示，那么它的俯视图是(      )

     A．    B．    C．   D．

02．(昆明)如图，这个几何体从上面看到的平面图形是(      )

03．(沈阳)如图所示，圆柱从上面看到的图形是图中的(      )

04．(成都)如图是由一些完全相同的小立方块搭成的几何体从正面、左面、上面看到的图形，那么搭成这  个几何体所用的小立方块的个数是(      )

A．3个  B．6个  C．7个  D．8个

从正面看   从左面看   从上面看

【例3】 (湛江)将如右图所示的Rt△ABC绕直角边BC旋转一周，所得几何体从左面看到的是(      )

【解法指导】 以直角三角形的直角边AC、BC为旋转轴得到的都是圆锥，故选择A．

【变式题组】

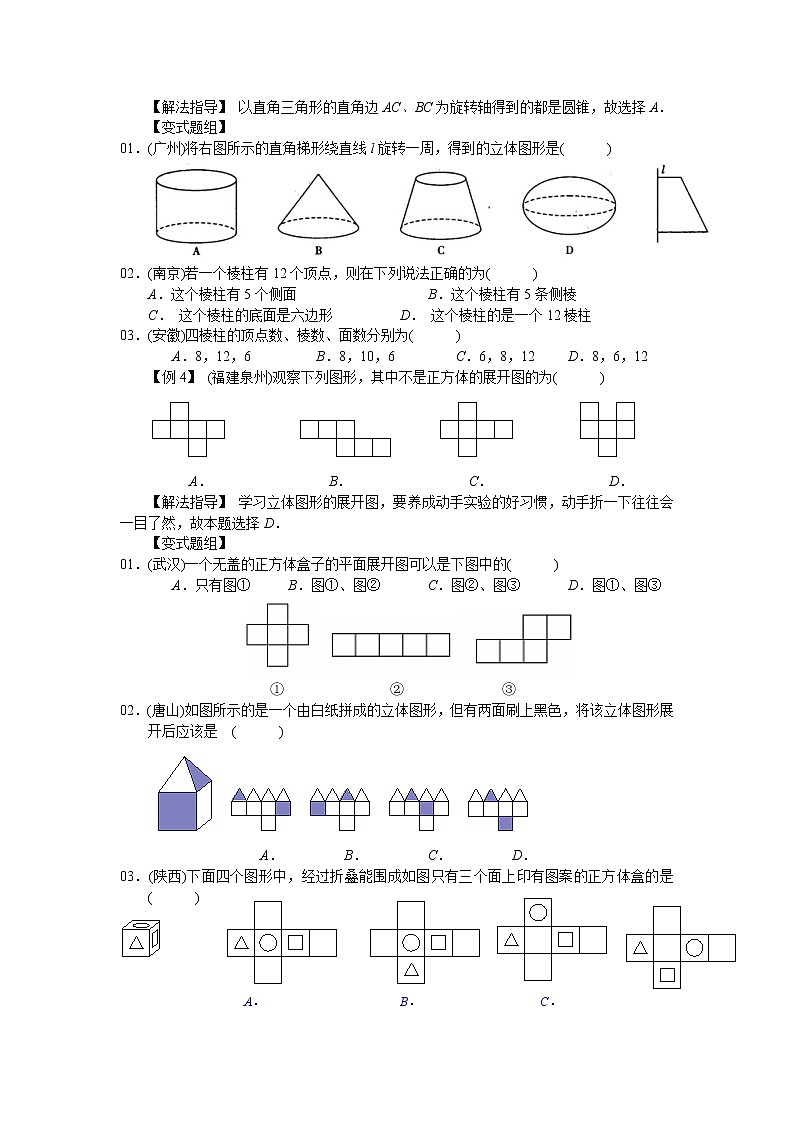
01．(广州)将右图所示的直角梯形绕直线l旋转一周，得到的立体图形是(      )

02．(南京)若一个棱柱有12个顶点，则在下列说法正确的为(      )

A．这个棱柱有5个侧面     B．这个棱柱有5条侧棱

C． 这个棱柱的底面是六边形   D． 这个棱柱的是一个12棱柱

03．(安徽)四棱柱的顶点数、棱数、面数分别为(      )

A．8，12，6   B．8，10，6   C．6，8，12  D．8，6，12

【例4】 (福建泉州)观察下列图形，其中不是正方体的展开图的为(      )

A．     B．     C．     D．

【解法指导】 学习立体图形的展开图，要养成动手实验的好习惯，动手折一下往往会一目了然，故本题选择D．

【变式题组】

01．(武汉)一个无盖的正方体盒子的平面展开图可以是下图中的(      )

A．只有图①  B．图①、图②  C．图②、图③  D．图①、图③

①    ②    ③

02．(唐山)如图所示的是一个由白纸拼成的立体图形，但有两面刷上黑色，将该立体图形展开后应该是 (      )

    A．   B．   C．   D．

03．(陕西)下面四个图形中，经过折叠能围成如图只有三个面上印有图案的正方体盒的是(      )

A．     B．     C．    D．

04．(北京)如图所示是三棱柱纸盒，在下面四个图中，只有一个是这个纸盒的展开图，那么这个展开图是 (      )

A．    B．    C．    D．

【例5】 (山西)一个画家有14个边长为1米的正方体，他在地面上把它们摆成如右图的形状，然后他把                                          露出的表面涂上颜色，那么被涂上颜色的总面积为(      )

A．19平方米  B．21平方米  C．33平方米  D．34平方米

【解法指导】 本题把涂上颜色的面积一块一块加起来计算很麻烦，应从整体角度出发，把立体转化为平面，观察题图所给的几何体，从前、后、左、右四个方向都只能看到6个1×1的正方形，从上面看可以看到一个3×3的大正方形轮廓，所以被涂上颜色的总面积应为4×6×1×1+3×3×1×1＝33(平方米)，故选C．

【变式题组】

01．(宜宾)如图是由若干个大小相同的小正方体堆砌而成的几何体．那么其三种视图中面积最小的是 (      )

A．正视图   B．左视图  C．俯视图  D．三种一样

02．(益阳)将一个底面直径为2 cm，高为2 cm的圆柱形纸筒沿一条母线剪开，所得到的侧面展开图的面积              为(      )

A．2πcm2  B．3πcm2  C．4πcm2  D．5πcm2

03．(青岛)一个大长方体是由四个完全一样的小长方体拼成的，如果每个小长方体的长、宽、高分别是3， 1，1那么这个大长方体的表面积可能有______种不同的值，其中最小值为______．

【例6】 (巴中)李明为好友制作一个(右图)正方形礼品盒，六个面上各有一字，连起来就是“预祝中考成功”，                            其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是(      )

【解法指导】 本例主要考查立方体的展开图中对面、邻面的分布规律，可动手折叠发现答案，故应选择C．

【变式题组】

01．(资阳)已知一个正方体的每一面都填有唯一一个数字，且各相对面上所填的数互为倒数，若这个正方  体的平面展开图如右图所示，则A、B的值分别是(      )

A．，   B． ，1   C．，   D．1，

02．(南宁)在下图中添加一个小正方形，使该图经过折叠后能围成一个四棱柱，不同的添法共有(      )

A．7种  B．4种  C．3种   D．2种

03．(沈阳)将一张长与宽的比为2：1的长方形纸片按如图①、②所示的方式对折后，然后沿图③中的虚线裁剪，得到图④，最后将图④的纸片再展开铺平，则所得到的图案是(      )

【例7】 (第21届江苏省竞赛题)设5 cm×4 cm×3 cm长方体的一个表面展开图的周长为n cm，则n的最                            小值是______．

【解法指导】 把展开图的周长用相应的代数式表示．长方体的展开图的周长为8c +4b +2a．故周长最小值为8×3+4×4+2×5＝50，故填50 cm．

【变式题组】

01．(广州)将一个长方形绕它的一边所在的直线旋转一周，得到的几何体是圆柱，如图现有一个边长为4  厘米，宽为3厘米的长方形，分别绕它的长、宽所在的直线旋转一周，得到不同的圆柱体，它们的体              积分别是多大?

02．(南京)如图是几个小立方块所搭成的几何体．从上面看图形，小正方形中的数字表示该位置的小立方  块的个数，那么是这个几何体从正面看的图形的是(      )

A．    B．    C．    D．

03．(烟台)如图①是由若干个小正方体所搭成的几何体， ②是①从上面看到的图形，则①从左面看到的图              形是(      )

①   ②    A．   B．   C．   D．

演练巩固 反馈提高

01．(连云港)水平位置的下列几何体，从正面看的图形不是长方形的是(      )

02．(邯郸)有一个外观为圆柱形的物体，它的内部构造从外部看不到，当分别用一组平面沿水平方向(自上 而下)和竖直方向(自左而右)截这个物体时(如图)，得到了如图所示的(1)、(2)两组形状不同的截面，则              这个物体的内部构造是(      )

A．空心圆柱  B．空心圆锥  C．空心球  D．空心半球

03．(唐山)将如图所示图形折叠成立方体后，下面四个选项正确的是(      )

04．(河南)由一些大小相同的小正方体组成的几何体的俯视图如图所示，其中正方形的数字表示在该位置  上的小正方体的个数，那么，这个几何体的左视图是(      )

A．    B．    C．    D．

05．(湖州)一个正方体的表面展开图如图所示，则原正方体中的“★”所在面的对面所标的字是(      )

A．上  B．海  C．世  D．博

006．(芜湖)一个几何体的三视图如图所示，那么这个几何体是(      )

A．    B．    C．    D．

07．(安徽)如图，下列四个几何体中，其主视图、左视图、俯视图中只有两个相同的是(      )

08．(哈尔滨)如下图所示的某一几何体的三视图，则这个几何体是(      )

A．圆柱  B．圆锥  C．正方体  D．球

正视图   左视图   俯视图

09．(泰州)如图是一个几何体的三视图，根据图中提供的数据(单位： cm)可求得这个几何体的体积为 (      )

A．2 cm2  B．4 cm2  C．6 cm2  D．8 cm2

主视图    左视图    俯视图

10．如图所示是无盖长方体盒子的表面展开图(重叠部分不计)则盒子的容积为(      )

A．4  B．6  C．12  D．15

11．(宜黄)宜黄素有“华南虎之乡”的美誉，将“华南虎之乡美”六个字填写在一个正方体的六个面上，其平              面展开图如图所示，那么在该正方体中，和“虎”字相对的字是______．

12．(黄冈)如图是由棱长为1的正方体搭成的积木三视图，则图中棱长为1的正方体的个数是______．

主视图    左视图    俯视图

13． 设有一个边长为1的正三角形，记作A1，将A1的每条边三等分， 在中间的线段上向外作正三角形，              去掉中间的线段后所得到的图形记作A2；将A2的每条边三等分， 重复上述过程，所得到的图形记作              A3，现将A3的每条边三等分，重复上述过程，所得到的图形记作A4，则A4的周长是多少?

14．(温州)由3个相同的小立方块搭成的几何体如图所示，请画出它的主视图和俯视图．

15．一个五棱柱如图，它的底面边长都是4厘米，侧棱长6厘米，回答下列问题．

 (1)这个五棱柱一共有多少个面?它们分别是什么形状?哪些面的形状、面积完全相同？

 (2)这个五棱柱一共有多少条棱?它们的长度分别是多少?

培优升级 奥赛检测

01．(成都)如图表示一个由相同小立方块搭成的几何体的俯视图，小正方形中的数字表示该位置上小立方  块的个数，那么该几何体的从正面看到的图形为(      )

A．    B．    C．    D．

02．(鄂尔多斯)将圆柱形纸筒沿母线AB剪开铺平，得到一个矩形(图1)；如果将这个纸筒沿线路BMA(图              2)剪开铺平，得到的图形是(      )

 A．平行四边形  B．矩形  C．三角形  D．半圆

03．(长春)一根单线从纽扣的4个孔中穿过(每个孔只穿过一次)，其正面情形如图所示，下面4个图形可能 是其背面情形的是(      )

04．(河北)用M、N、P、Q各代表四种简单几何图形(线段、正三角形、正方形、圆)中的一种，下图①至                            ④是由M、N、P、Q中的两种图形组合而成的(组合用“&”表示)．那么下列组合图形表示P&Q的是              (      )

05． (第11届“华罗庚杯”竞赛试题)如图是一个立体图形的主视图，左视图(图中单位为厘米)，则立体图形                            的体积为(      )立方厘米．

A．π  B．2π  C．3π  D．4π

06．(太原)如下左图是一个正方体的平面展开图，这个正方体是(      )

A．    B．    C．    D．

07．(第18届“希望杯”邀请赛试题)某人特制了4个同样的立方块，并将它们如图(a)放置，然后又如图(b)                            放置，则图(b)中四个底面正方形中的点数之和为(      )

A．11  B．13  C．14  D．16

08．(重庆市竞赛题)把10个相同的小正方形按如图的位置堆放，它的外表会有若干个小正方形，如果将图 中标有字母P的一个小正方体搬去，这时外表含有的小正方形的个数与搬运前相比(      )

A．不增不减  B．减少1个  C． 减少2个  D． 减少3个

09．(威海)如图，可以沿线折叠成一个带数字的立方体，每三个带数字的面交于立方体的一个顶点，则相  交于一个顶点的三个面上的数字之和最小值是______．

10．(第21届江苏省竞赛)设5 cm ×4 cm ×3 cm长方体的一个表面展开图的周长为n cm，则n的最小值              是______．

11．画出如图的几何体从正面、上面、左面看到的平面图形．

12．下面图形如图，线直线l旋转一周后形成什么图形?

13．(杭州)已知直四棱柱的底面是边长为a的正方形，高为h，体积为V，表面积等于S．

 (1)当a＝2， h＝3时，分别求V和S；

 (2)当V＝12，S＝32时，求+的值．