








初中人教版 (五四制)30.2 中心对称精品课件ppt
展开30.2.2 中心对称图形
一、教学目标
(一)学习目标
1.了解中心对称图形的概念及中心对称图形的对称中心的概念,掌握这两个概念的应用.
2.复习两个图形关于中心对称的有关概念,利用这个所学知识探索一个图形是中心对称图形的有关概念及其它的运用.
(二)学习重点
中心对称图形的有关概念及其它们的运用.
(三)学习难点
区别关于中心对称的两个图形和中心对称图形.
二、教学设计
(一)课前设计
1.预习任务
(1)中心对称图形的定义:把一个图形绕着某个点旋转,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
(2)中心对称图形的性质:
①图形上每一对对应点所连接成的线段都过对称中心,且被对称中心平分.
②对应线段相等且平行(或共线).
2.预习自测
(1)下列图案中,不是中心对称图形的是( )
A. B. C. D.
【知识点】中心对称图形的定义.
【解题过程】观察旋转180°后完全重合.则选B.
【思路点拨】抓住中心对称图形的定义.
【答案】B.
(2)下列说法正确的是( )
A. 关于中心对称的两个图形全等 B. 全等的两个图形是中心对称图形
C. 中心对称图形都是轴对称图形 D. 轴对称图形都是中心对称图形
【知识点】中心对称和中心对称图形的定义
【解题过程】利用中心对称定义可判断,选A.
【思路点拨】抓住中心对称图形的定义
【答案】A.
(3)连接中心对称图形上两个对应点的线段,经过 ,且 .
【知识点】中心对称图形的性质
【解题过程】利用中心对称图形的性质:对称中心;被对称中心平分.
【思路点拨】抓住中心对称图形的性质
【答案】对称中心;被对称中心平分.
(4)把O L Y M P I C每个字母都看成一个图形,那么中心对称图形是 .
【知识点】中心对称图形的性质
【解题过程】由中心对称图形的性质可得:O,I.
【思路点拨】抓住中心对称图形的性质
【答案】 O,I.
(二)课堂设计
1.知识回顾
(1)中心对称的定义:如果把一个图形绕某个点旋转,它能够与另一个图形重合,那么这两个图形关于这个点对称或中心对称.这个点叫做它们的对称中心.这两个图形中的对应点叫做关于中心的对称点.
(2)中心对称的性质:
1.中心对称的两个图形,对称点所连线段必过对称中心,且被对称中心平分.
2.中心对称的两个图形是全等图形.
2.问题探究
探究一 中心对称图形及中心对称图形的对称中心的相关概念 重点知识★
●活动① 回顾旧知,回忆中心对称中的相关概念
1.师:关于中心对称的两个图形具有什么性质?
生:关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.
关于中心对称的两个图形是全等图形.
2.(学生活动)作图题.
作出三角形AOB关于O点的对称图形,如图所示.
解:延长AO使OC=AO,
延长BO使OD=BO,
连结CD
则△COD为所求的,如图所示.
【设计意图】通过对旧知识的复习,为新知识的学习作铺垫.
●活动② 整合旧知,探究中心对称图形中的相关概念.
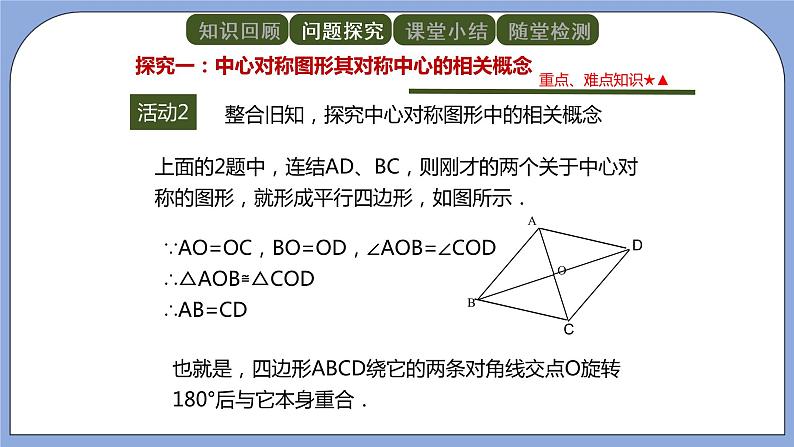
上面的2题中,连结AD、BC,则刚才的两个关于中心对称的图形,就形成平行四边形,如图所示.
∵AO=OC,BO=OD,∠AOB=∠COD
∴△AOB≌△COD
∴AB=CD
也就是,四边形ABCD绕它的两条对角线交点O旋转180°后与它本身重合.
像这样,把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.
【设计意图】鼓励学生独立自主解决问题,让学生初步感受通过观察来掌握几何知识的相关概念,引导学生由观察得到感性认识,思考满足中心对称图形的条件,寻求解决问题的方法.
探究二 中心对称图形的基本性质 重点、难点知识★▲
●活动① (大胆猜想,大胆操作,探究新知识)
如图,四边形ABCD绕O点旋转180°,与原图完全重合.
(1)这个图形是中心对称图形吗?如果是对称中心是哪一点?如果不是,请说明理由.
(2)如果是中心对称图形,那么A、B、C、D关于中心的对称点是哪些点.
解:⑴根据中心对称图形的定义便知这个图形是中心对称图形,对称中心是O点.
⑵A、B、C、D关于中心O的对称点是C、D、A、B.
【设计意图】老师综合学生的疑惑,把有意义的问题归纳,并展示出来.
●活动② (集思广益,探索中心对称图形的基本性质)
如图,线段AB绕中点O旋转180°,与原图完全重合;
平行四边形ABCD绕O点旋转180°,与原图完全重合.
则线段AB与平行四边形ABCD均为中心对称图形.
图(1)中,A、B、O共线,且OA=OB;
图(2)中,A、C、O共线,B、D、O共线,且OA=OC,OB=OD;AB=CD,AD=BC.
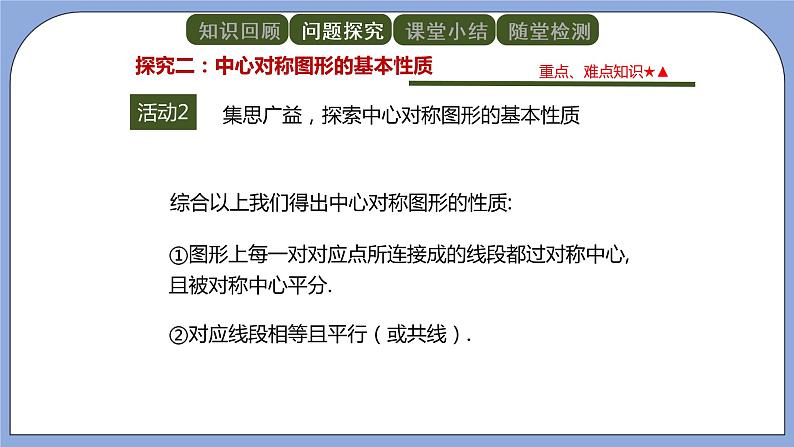
因此,综合以上我们得出中心对称图形的性质:
①图形上每一对对应点所连接成的线段都过对称中心,且被对称中心平分.
②对应线段相等且平行(或共线).
【设计意图】通过中心对称图形的定义,发现并证明中心对称图形的性质.
●活动③ (中心对称图形的性质应用)
1.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,涂黑的小正方形的序号是 .
【知识点】中心对称图形的定义
【数学思想】数形结合
【解题过程】四个位置依次尝试,只有②可以.
【思路点拨】抓住中心对称图形的定义
【答案】②.
【设计意图】进一步理解中心对称图形的定义
2.四张扑克牌如图①所示放在桌面上,小敏把其中一张旋转180°后得到图②,则她所旋转的牌从左数起是( )
- 第一张 B. 第二张 C. 第三张 D. 第四张
【知识点】中心对称图形的性质
【解题过程】由旋转180°观察是否重合,故选A.
【思路点拨】抓住中心对称图形的性质
【答案】A.
【设计意图】中心对称图形的性质应用
●活动④ (对比探究)
中心对称与中心对称图形的区别与联系.
成中心对称 中心对称图形
①一个图形与另一个图形重合 一个图形与本身重合
②两个图形的位置关系 一个图形本身的性质
探究三 拓展应用 ★ ▲
●活动① (中心对称图形识图)
例1. 下列图形中,既是轴对称,又是中心对称图形的是( )
A B C D
【知识点】中心对称图形和轴对称图形的定义.
【解题过程】由中心对称图形的定义可得D.
【思路点拨】抓住中心对称图形的性质是解题的关键.
【答案】D.
练习:下列图形中,既是轴对称图形又是中心对称图形的有( )
A. 4个 B. 3个 C. 2 个 D. 1 个
【知识点】中心对称图形和轴对称图形的定义.
【解题过程】由中心对称图形的定义可得C.
【思路点拨】抓住中心对称图形的性质是解题的关键.
【答案】C.
【设计意图】通过训练,进一步掌握中心对称图形的定义.
●活动2 (提升型例题)
例2.下列正多边形绕中心至少旋转多少度与原图重合.
【知识点】旋转对称图形
【解题过程】令相邻两个顶点首次重合的角度即为所求,分别是120°,90°,72°,60°.
【思路点拨】正n边形绕中心至少旋转与原图重合.
【答案】120°,90°,72°,60°.
练习:下列图形绕中心至少旋转多少度与原图重合.
【知识点】旋转对称图形
【解题过程】令相邻两个顶点首次重合的角度即为所求,分别是72°,120°,90°,120°.
【思路点拨】抓住几个顶点旋转重合即可
【答案】72°,120°,90°,120°.
【设计意图】通过训练,进一步掌握中心对称图形的性质
●活动3 (探究型例题)
例3.各基本图形的对称性:
| 轴对称 | 中心对称 |
直线、线段 |
|
|
等腰三角形 |
|
|
等边三角形 |
|
|
平行四边形 |
|
|
菱形 |
|
|
矩形 |
|
|
正方形 |
|
|
【知识点】轴对称和中心对称的定义
【解题过程】由轴对称和中心对称的定义可得:
| 轴对称 | 中心对称 |
直线、线段 | 是 | 是 |
等腰三角形 | 是 | 不是 |
等边三角形 | 是 | 不是 |
平行四边形 | 不是 | 是 |
菱形 | 是 | 是 |
矩形 | 是 | 是 |
正方形 | 是 | 是 |
【思路点拨】抓住轴对称和中心对称的定义
【答案】
| 轴对称 | 中心对称 |
直线、线段 | 是 | 是 |
等腰三角形 | 是 | 不是 |
等边三角形 | 是 | 不是 |
平行四边形 | 不是 | 是 |
菱形 | 是 | 是 |
矩形 | 是 | 是 |
正方形 | 是 | 是 |
练习:判断以下命题是否是真命题.
①关于轴对称的两个图形全等 ②关于中心对称的两个图形全等
③等边三角形既是轴对称图形,又是中心对称图形
④矩形既是轴对称图形,又是中心对称图形
⑤轴对称图形一定是中心对称图形
⑥中心对称图形一定是轴对称图形
⑦有两条互相垂直对称轴的轴对称图形一定是中心对称图形
【知识点】轴对称和中心对称的性质
【解题过程】
③等边三角形是轴对称图形,不是中心对称图形;
⑤轴对称图形不一定是中心对称图形;
⑥中心对称图形不一定是轴对称图形.
即真命题:①②④⑦;假命题:③⑤⑥.
【思路点拨】抓住轴对称和中心对称的性质
【答案】真命题:①②④⑦;假命题:③⑤⑥.
【设计意图】综合运用中心对称图形的性质解题
3. 课堂总结
知识梳理
(1)中心对称图形的定义:把一个图形绕着某个点旋转,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
(2)中心对称图形的性质:
①图形上每一对对应点所连接成的线段都过对称中心,且被对称中心平分.
②对应线段相等且平行(或共线).
重难点归纳
⑴中心对称图形的有关概念及其它们的运用.
⑵区别关于中心对称的两个图形和中心对称图形.
(三)课后作业
基础型 自主突破
1.下列图形中,既是轴对称图形又是中心对称图形的是( )
A. 等边三角形 B. 平行四边形 C. 正五边形 D. 菱形
【知识点】轴对称和中心对称的定义
【解题过程】A轴对称,B中心对称,C轴对称,所以选D.
【思路点拨】抓住轴对称和中心对称的定义
【答案】D.
2.线段是中心对称图形,对称中心是 ;平行四边形也是中心对称图形,对称中心是 .
【知识点】中心对称图形的性质
【解题过程】由中心对称图形的性质可得:线段中点;两条对角线的交点
【思路点拨】抓住中心对称图形的性质
【答案】线段中点;两条对角线的交点
3.下列四个艺术字中,不是中心对称图形的是( )
A. 木 B. 田 C. 王 D. 噩
【知识点】中心对称图形的性质
【解题过程】由中心对称图形的定义可知,选A.
【思路点拨】抓住中心对称图形的性质
【答案】A.
4.已知六边形ABCDEF是中心对称图形,AB=1,BC=2,CD=3,那么EF= .
【知识点】中心对称图形的性质
【解题过程】EF与BC是对应边,故 EF=BC=2.
【思路点拨】抓住中心对称图形的性质
【答案】2.
5.在四边形ABCD中,AB=CD,要使四边形ABCD是中心对称图形,只需添加一个条件,这个条件可以是 .
【知识点】中心对称图形的性质
【解题过程】根据平行四边形是中心对称图形,可以针对平行四边形的各种判定方法,给出相应的条件,得出此四边形是中心对称图形.即可添加:AD=BC或AB∥CD或∠B+∠C=180°或∠A+∠D=180°等.
【思路点拨】抓住中心对称图形的性质
【答案】AD=BC或AB∥CD或∠B+∠C=180°或∠A+∠D=180°等.
6.如图所示,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD、BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为 .
【知识点】中心对称图形的性质
【解题过程】∵矩形是中心对称图形,
∴△AOE和△COF关于点O对称,
∴,
∴
【思路点拨】抓住中心对称图形的性质
【答案】3.
能力型 师生共研
- 下列图形:①平行四边形;②正方形;③等腰梯形;④菱形;⑤正六边形.其中既是轴对称图形又是中心对称图形的有( )
A .1个 B.2个 C.3个 D.4个
【知识点】中心对称图形;轴对称图形
【解题过程】平行四边形不是轴对称图形,是中心对称图形.故错误;
正方形是轴对称图形,也是中心对称图形.故正确;
等腰梯形是轴对称图形,不是中心对称图形.故错误;
菱形是轴对称图形,也是中心对称图形.故正确;
正六边形是轴对称图形,也是中心对称图形.故正确. 共3个.故选C.
【思路点拨】根据轴对称图形与中心对称图形的概念求解.
【答案】C.
8.在综合实践活动课上,老师组织大家利用两块大小相同的含30°角的三角板进行拼接组合(不重叠)的探索活动,在讨论所组合而成的图形过程中,所得下列四个结论中错误的是( )
A.当两块三角板的斜边完全拼接在一起时,所拼成的图形一定是轴对称图形
B.当两块三角板的对应直角边完全拼接在一起时,所拼成的图形可能是等边三角形
C.当两块三角板可以通过平移后重合时,所拼成的图形不可能是轴对称图形
D.当两块三角板只有直角顶点拼接在一起时,所拼成的图形不可能是中心对称图形
【知识点】中心对称和轴对称的性质
【解题过程】当两块三角板只有直角顶点拼接在一起时,所拼成的图形有可能是中心对称图
形,故D错误.即选D.
【思路点拨】抓住中心对称和轴对称的性质
【答案】D.
探究型 多维突破
9.如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形标号为
A. ①② B. ②③ C. ①③ D. ①②③
【知识点】中心对称图形的性质
【解题过程】
如图,设原住房平面图长方形的周长为2l,①的长和宽分别为a、b,②③的边长分别为c、d.
根据题意,得
①-②得a-c=c-b⇒a+b=2c,
将a+b=2c代入,得4c=l⇒2c=(定值),
将2c=代入a+b=2c,得a+b=⇒2(a+b)=l(定值),
而由已列方程组得不到d.
∴分割后不用测量就能知道周长的图形标号为①②.
【思路点拨】抓住中心对称图形的性质
【答案】A.
10.如图,在2×2的正方形网格纸中,有一个以格点为顶点的△ABC,请你找出网格纸中所有与△ABC成中心称且也以格点为顶点的三角形共有 个.(不包括△ABC本身)
【知识点】中心对称图形的性质
【解题过程】如图,与△ABC成中心对称的三角形有:①△ACG关于中心点I成中心对称;②△DFG关于中心点0成中心对称,共2个.
【思路点拨】抓住中心对称图形的性质
【答案】2.
自助餐
1.下列各图中,不是中心对称图形的是
A. B. C. D.
【知识点】中心对称图形的定义
【解题过程】B是轴对称图形,但不是中心对称图形,故选B.
【思路点拨】抓住中心对称图形的定义
【答案】B.
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
【知识点】中心对称图形的定义
【解题过程】D既是轴对称图形,又是中心对称图形,故选D.
【思路点拨】抓住中心对称图形的定义
【答案】D.
3.下面的几何图形中,既是轴对称图形又是中心对称图形的个数是
A.4 B.3 C.2 D.1
【知识点】轴对称图形和中心对称图形的定义
【解题过程】等腰三角形,等腰梯形,正五边形是轴对称图形,但不是中心对称图形;
故选C.
【思路点拨】抓住轴对称图形和中心对称图形的定义
【答案】C.
4.如图所示,四边形ABCD是中心对称图形,对称中心为点O,过点O的直线与AD、BC分别交于点E、F,则图中相等的线段有 对.
【知识点】中心对称图形的性质
【解题过程】AB=CD,AD=BC,AE=CF,BF=DE,OE=DE.即有5对.
【思路点拨】抓住中心对称图形的性质
【答案】5.
5.将正方体骰子(相对面上的点数分别为 1 和 6 、 2 和 5 、 3 和 4 )放置于水平桌面上 ,如图 ① .在图 ② 中,将骰子向右翻滚,然后在桌面上按逆时针方向旋转,则完成一次变换.若骰子的初始位置为图①所示的状态,那么按上述规则连续完成10次变换后,骰子朝上一面的点数是( )
A.6 B.5 C.3 D.2
【知识点】旋转的性质
【解题过程】一次变换后5朝上,二次变换后6朝上,三次变换后3朝上,四次变换后5朝上(此时同第一次变换),三次一个循环,所以10次变换后是5朝上,选B.
【思路点拨】抓住旋转图形的性质
【答案】B.
6.下列3×3网格都是由9个相同小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(请将三个小题 依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
【知识点】轴对称图形和中心对称图形的性质
【解题过程】(1) 画出下列其中一种即可.
(2) 画出下列其中一种即可.
(3) 画出下列其中一种即可.
【思路点拨】抓住轴对称图形和中心对称图形的性质
【答案】(1) 画出下列其中一种即可.
(2) 画出下列其中一种即可.
(3) 画出下列其中一种即可.
初中32.3 用频率估计概率精品ppt课件: 这是一份初中32.3 用频率估计概率精品ppt课件,文件包含人教版五四学制九上数学323用频率估计概率课件pptx、人教版五四学制九上数学323用频率估计概率教案doc等2份课件配套教学资源,其中PPT共40页, 欢迎下载使用。
初中数学人教版 (五四制)九年级上册32.1 随机事件与概率公开课ppt课件: 这是一份初中数学人教版 (五四制)九年级上册32.1 随机事件与概率公开课ppt课件,文件包含人教版五四学制九上数学3212概率课件ppt、人教版五四学制九上数学3212概率教案doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
初中数学人教版 (五四制)九年级上册第32章 概率初步32.1 随机事件与概率优秀ppt课件: 这是一份初中数学人教版 (五四制)九年级上册第32章 概率初步32.1 随机事件与概率优秀ppt课件,文件包含人教版五四学制九上数学3211随机事件课件ppt、人教版五四学制九上数学3211随机事件教案doc等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。













