沪科版九年级上册21.1 二次函数优秀课件ppt

这是一份沪科版九年级上册21.1 二次函数优秀课件ppt，共20页。PPT课件主要包含了学习目标及重难点，课程导入，0-5，直线x-2，-2-4，直线x4，课程讲授，x-2，对称轴，顶点坐标等内容，欢迎下载使用。

1.会用配方法或公式法将一般式 y＝ax2＋bx＋c 化成顶点式y=a(x-h)2+k；（重点）2.会熟练求出一般式 y＝ax2＋bx＋c 的顶点坐标、对称轴.（难点）
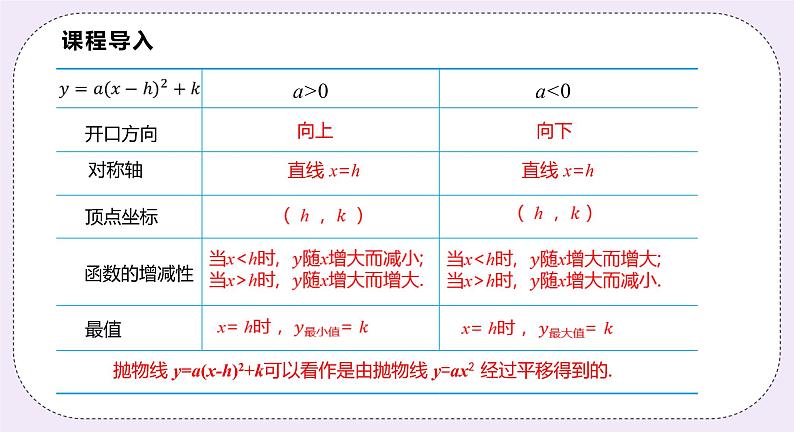
抛物线 y=a(x-h)2+k可以看作是由抛物线 y=ax2 经过平移得到的.
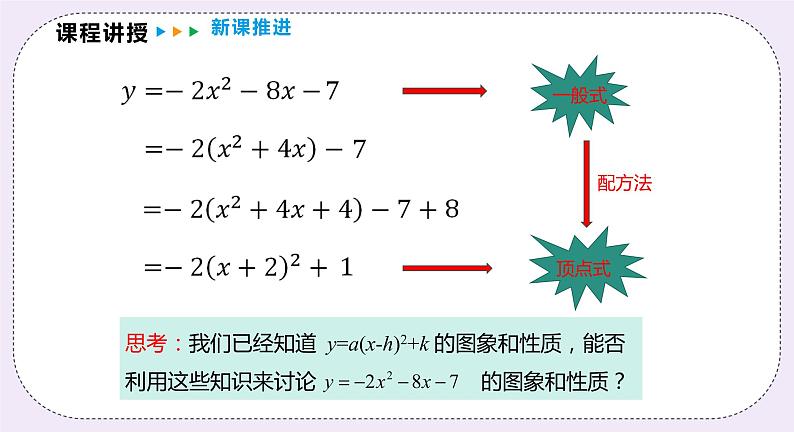
例1 怎样将 化成 y=a(x-h)2+k 的形式
(1)“提”：提出二次项系数；
(2)“配”：括号内配成完全平方；
(3)“化”：化成顶点式.
提示:配方后的表达式通常称为配方式或顶点式.
答：对称轴是直线 x=-2,顶点坐标是（-2，1）.
答：平移方法1 先向上平移1个单位，再向左平移2个单位得到的； 平移方法2 先向左平移2个单位，再向上平移1个单位得到的.
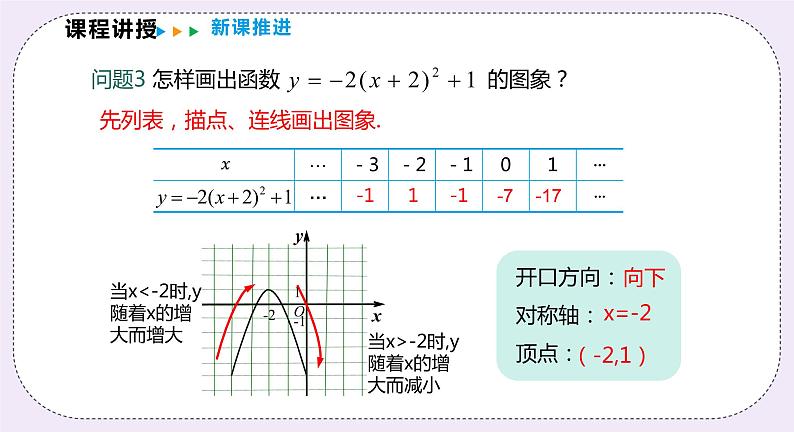
先列表，描点、连线画出图象.
当x<-2时,y随着x的增大而增大
当x>-2时,y随着x的增大而减小
二次函数 的图象如下图所示，请根据二次函数的性质填空：
探索：二次函数字母系数与图象的关系
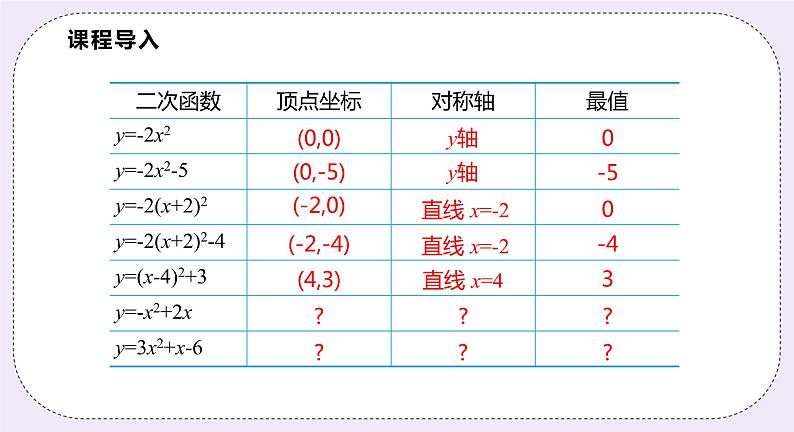
例2 根据公式确定下列二次函数图象的对称轴和顶点坐标：
习题2 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示，则下列结论：
（1）a、b同号；（2）当x=–1和x=3时，函数值相等；（3） 4a+b=0；（4）当y=–2时，x的值只能取0；其中正确的是 .