河南省商丘市柘城县2021-2022学年七年级下学期期中质量检测数学试卷(含解析)

河南省商丘市柘城县2021-2022学年下学期七年级期中

数学考试题

一、选择题

1. 面积为4的正方形的边长是（      ）

A. 4的平方根 B. 4的算术平方根 C. 4开平方的结果 D. 4的立方根

2. 如图，已知，为角平分线，下列说法错误的是（    ）

A  B.  

C.  D.

3. 已知，则在如图所示的平面直角坐标系中，小手盖住的点的坐标可能是（    ）

A.  B.  

C.  D.

4. 在，，，，，0. 2020020002…（两个“2”之间依次多一个“0”），，，中无理数的个数是(   )

A. 4个 B. 5个 C. 6个 D. 7个

5. 下列说法中，正确的是(   )

A. 的平方根是4 B. 9的算术平方根是

C. 的立方根是 D. 的平方根是

6. 估计的值在（    ）

A. 2到3之间 B. 3到4之间 C. 4到5之间 D. 5到6之间

7. 将一把直尺和一块含30°角的三角板ABC按如图所示的位置放置，如果∠CED＝46°，那么∠BAF的度数为（　　）

A. 48° B. 16° C. 14° D. 32°

8. 如图，点在的延长线上，于点，交于点．若，则的度数为（    ）．

A. 65° B. 70° C. 75° D. 85°

9. 已知M（1，﹣2），N（﹣3，﹣2），则直线MN与x轴，y轴的位置关系分别为（ ）

A. 相交，相交 B. 平行，平行

C. 垂直，平行 D. 平行，垂直

10. 若和两边分别平行，且比的两倍少，则的度数为(   )

A.  B.  C. 或 D.

二、填空题

11. 无理数的整数部分是_____，小数部分是_____．

12. 如图是小凡同学在体育课上跳远后留下的脚印，他的跳远成绩是线段   _______的长度，这样测量的依据是____________________．

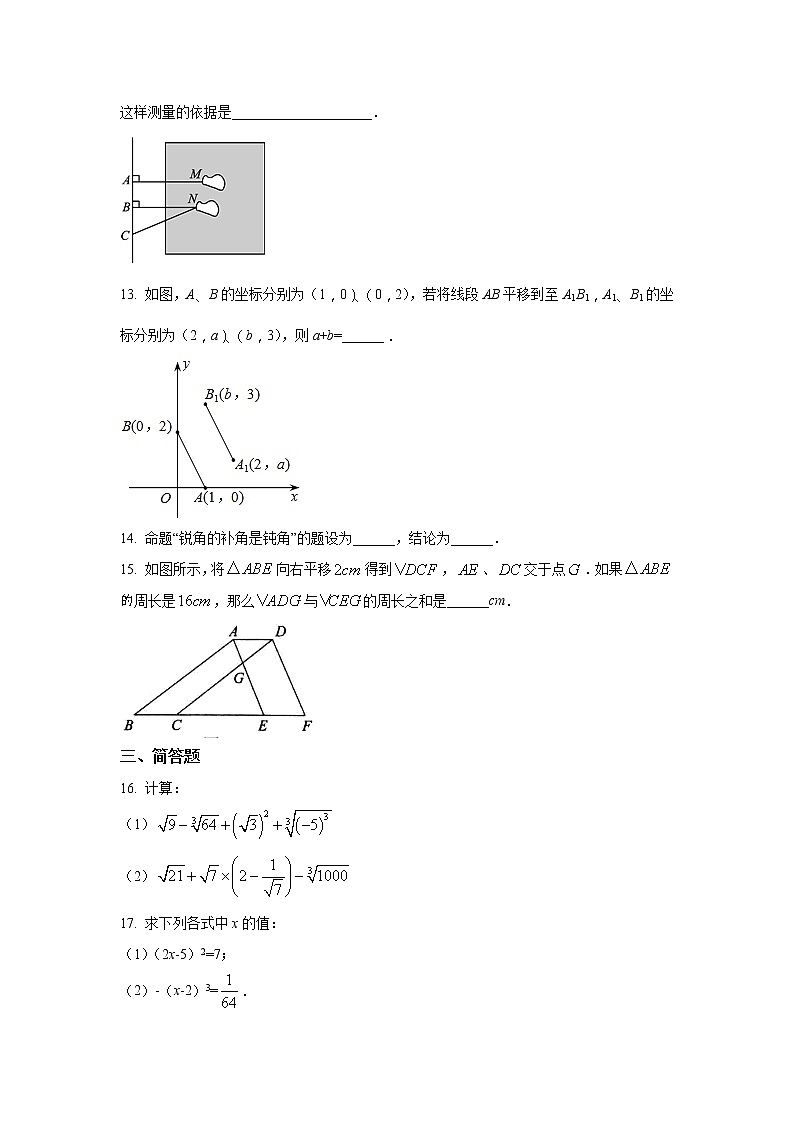
13. 如图，A、B的坐标分别为（1，0）、（0，2），若将线段AB平移到至A1B1，A1、B1的坐标分别为（2，a）、（b，3），则a+b=______．

14. 命题“锐角的补角是钝角”的题设为______，结论为______．

15. 如图所示，将向右平移得到，、交于点．如果周长是，那么与的周长之和是______cm．

三、简答题

16. 计算：

（1）

（2）

17. 求下列各式中x的值：

（1）（2x-5）2=7；

（2）-（x-2）3=．

18. 已知实数a，b，c，d，e，f，且a，b互为倒数，c，d互为相反数，e的绝对值为，f的算术平方根是8，求ab＋＋e2＋的值．

19. 如图，有下列三个条件：①DE//BC；②；③．

（1）若从这三个条件中任选两个作为题设，另一个作为结论，组成一个命题，一共能组成几个命题？请你都写出来；

（2）你所写出的命题都是真命题吗？若是，请你就其中的一个真命题给出推理过程；若不是，请你对其中的假命题举出一个反例（温馨提示：）

20. 如图，有一块不规则的四边形地皮ABCO，各个顶点的坐标分别为A(－2，6)，B(－5，4)，C(－7，0)，O(0，0)(图上一个单位长度表示10米)，现在想对这块地皮进行规划，需要确定它的面积．

(1)求这个四边形的面积；

(2)如果把四边形ABCD的各个顶点的纵坐标保持不变，横坐标加2，所得到的四边形面积是多少？

21. 如图，已知，，那么，为什么？请完成下列推理过程：

∵（已知），

又∵（                       ）．

∴（                       ）

∴__________________（                       ）．

∴（     ）（                       ）

∵（已知）．

∴_________=_________（等量代换）

∴（                       ）

22. 如图，直线AB，CD相交于点O，OF⊥CD，OE平分∠BOC．

（1）若∠BOE＝65°，求∠DOE度数；

（2）若∠BOD：∠BOE＝2：3，求∠AOF的度数．

23. 如图1，在平面直角坐标系中，点，的坐标分别是，，现同时将点，分别向上平移2个单位长度，再向右平移2个单位长度，得到，的对应点，，连接，，．

（1）点坐标为_________，点的坐标为_________，四边形的面积为_________；

（2）在轴上是否存在一点，使得的面积是面积的2倍？若存在，请求出点的坐标；若不存在，请说明理由．

（3）如图2，点是线段上一动点（，两点除外），试说明与的大小关系，并说明理由．

答案

1. B

解：面积为4的正方形的边长是，即为4的算术平方根；

故选B．

2. B

∵l1∥AB，

∴∠2=∠4，∠3=∠2，∠5=∠1+∠2，

∵AC为角平分线，

∴∠1=∠2=∠4=∠3，∠5=2∠1．

故选B．

3. B

∵

∴

选项Ａ：在第一象限

选项Ｂ：在第二象限

选项Ｃ：在第三象限

选项Ｄ：在第四象限

小手盖住的点位于第二象限

故选：B

4. B

解：∵=2，=-2，

∴在，，，，，0. 2020020002…（两个“2”之间依次多一个“0”），，，中，无理数有，，0.2020020002…（两个“2”之间依次多一个“0”），，，共5个，

故选：B．

5. C

解：A. 没有平方根，故该项错误；

B. 9的平方根是，故该项错误；

C. 的立方根是，故该项正确；

D. 9的平方根是，故该项错误；

故选：C．

6. C

解：∵，
∴

即

在4和5之间，
故选C．

7. C

解：∵DE∥AF，

∴∠CED＝∠EAF＝46°，

∵∠BAC＝90°﹣30°＝60°，

∴∠BAF＝∠BAC﹣∠EAF＝60°﹣46°＝14°，

故选：C．

8. B

解：∵

∴，

∴．

故选B．

9. D

由点M(1，－2)和点N(－3，－2)的纵坐标相等可知，直线MN平行于x轴，则与y轴垂直．或者在平面直角坐标系中描出点M和点N，结合图判断出直线MN平行于x轴，与y轴垂直．

10. C

解：∵∠A和∠B两边分别平行，

∴∠A=∠B或∠A+∠B=180°，

∵∠A比∠B的两倍少45°，

即∠A=2∠B-45°，

∴2∠B-45°=∠B或2∠B-45°+∠B=180°，

∴∠B=45°或∠B=75°

故选：C．

11. ①. 3    ②. ﹣5

∵25＜29＜36，

∴5＜＜6，

∴3＜-2＜4，

∴−2的整数部分是3，小数部分是为-2-3=-5．

故答案为3；-5．

12. ①. 3    ②. ﹣5

∵25＜29＜36，

∴5＜＜6，

∴3＜-2＜4，

∴−2的整数部分是3，小数部分是为-2-3=-5．

故答案为3；-5．

13. 2

解：根据点的坐标可得：图象先向右平移1个单位，再向上平移1个单位，

则a=1+0=1，b=1+0=1，

则a+b=1+1=2．

故答案为：2．

14. ①. 如果一个角是锐角的补角    ②. 那么这个角是钝角

解：题设为：一个角是锐角的补角，结论为：这个角是钝角，故写成“如果…那么…”的形式是：如果一个角是锐角的补角，那么这个角是钝角，

故答案为：如果一个角是锐角的补角，那么这个角是钝角．

15. 16

∵△ABE向右平移2cm得到△DCF，
∴DF=AE，
∴△ADG与△CEG的周长之和=AD+CE+CD+AE=BE+AB+AE=16，
故答案为：16；

16. （1）

=3－4+3－5

=－3．

（2）

．

17. （1）

解：方程两边开平方，得2x-5=±

则2x=5+，或2x=5-

解得x=或x=

（2）

方程两边同乘-1，得（x-2）3=-

方程两边开立方，得x-2=-

解得x=．

18. 解：由题意可知：ab＝1，c＋d＝0，e＝±，f＝64，

∴e2＝(±)2＝2，＝=4.

∴ab＋＋e2＋＝＋0＋2＋4＝6．

19. （1）

解：一共能组成三个命题：

①如果DE//BC，，那么；

②如果DE//BC，，那么；

③如果，，那么DE//BC ；

（2）

解：都是真命题，

如果DE//BC，，那么，

理由如下：∵DE//BC，

∴，

∵，

∴．

如果DE//BC，，那么；

理由如下：∵DE//BC，

∴，，

∵，

∴；

如果，，那么DE//BC ；

理由如下：∵，

∴∠B+∠C=180°-∠BAC，

∵∠1+∠2+∠BAC=180°，

∴∠1+∠2=180°-∠BAC，

∴∠B+∠C=∠1+∠2，

∵，，

∴∠B=∠1，

∴DE//BC ．

20. 解：

(1)过B作BF⊥x轴于F，过A作AG⊥x轴于G，如图所示．

∴S四边形ABCO＝S三角形BCF＋S梯形ABFG＋S三角形AGO

＝[]

×102＝2500(平方米)．

(2)把四边形ABCO的各个顶点的纵坐标保持不变，横坐标加2，即将这个四边形向右平移2个单位长度，

故所得到的四边形的面积与原四边形的面积相等，为2500平方米．

21. 对顶角相等；等量代换；；；同位角相等，两直线平行；；两直线平行，同位角相等；；；内错角相等，两直线平行．

22. （1）∵OE平分∠BOC，∠BOE=65°，

∴∠EOC=∠BOE=65°，

∴∠DOE=180°-∠EOC=180°-65°=115°；

（2）∵OE平分∠BOC，

∴∠EOC=∠BOE，

∵∠BOD:∠BOE=2:3，

设∠BOD=x，则∠COE=∠BOE=，

∵∠COE+∠BOE+∠BOD=180°，

∴，

∴x=45°，

∵OF⊥CD，∠BOD=∠AOC，

∴∠BOD=∠AOC=45°，

∴∠COF=90°，

∴∠AOF=∠COF-∠AOC=90°-45°=45°.

23. （1）

解：∵点A、的坐标分别是，，同时将点、分别向上平移2个单位长度，再向右平移2个单位长度得到A、的对应点、，

∴点的坐标为，点的坐标为，

；

（2）

解：存在．理由如下：

设点的坐标为，

∵的面积是的面积的2倍，

∴，解得或，

∴点的坐标为或；

（3）

解：，理由如下：

过点作交轴于，如图所示：

∴

∴，，

∴．