高考复习 2.1　函数的概念及其表示课件PPT

这是一份高考复习 2.1　函数的概念及其表示课件PPT，共44页。PPT课件主要包含了实数集，唯一确定，定义域，对应关系，答案B，答案C，答案D，x＋1，－31，－11等内容，欢迎下载使用。

【课标标准】　1.了解构成函数的要素，会求一些简单函数的定义域.2.在实际情境中，会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.3.了解简单的分段函数，并能简单应用．
知识梳理1.函数的概念一般地，设A，B是非空的________，如果对于集合A中的________一个数x，按照某种确定的对应关系f，在集合B中都有________的数y和它对应，那么就称f：A→B为从集合A到集合B的一个函数，记作y＝f(x)，x∈A.2．函数的三要素(1)函数的三要素：________、________和________．(2)两个函数只有当________和________分别相同时，这两个函数才相同．
3．函数的表示法表示函数的常用方法有解析式法、列表法、图象法．4．分段函数在一个函数的定义域中，对于自变量x的不同取值范围，有着不同的对应关系，这样的函数叫分段函数．
夯实双基1.思考辨析(正确的打“√”，错误的打“×”)(1)函数y＝f(x)的图象可以是一条封闭的曲线．(　　)(2)直线x＝1与函数y＝f(x)的图象的交点最多有两个．(　　)(3)函数y＝1与y＝x0是同一个函数. (　　)(4)若两个函数的定义域与值域相同，则这两个函数相等．(　　)
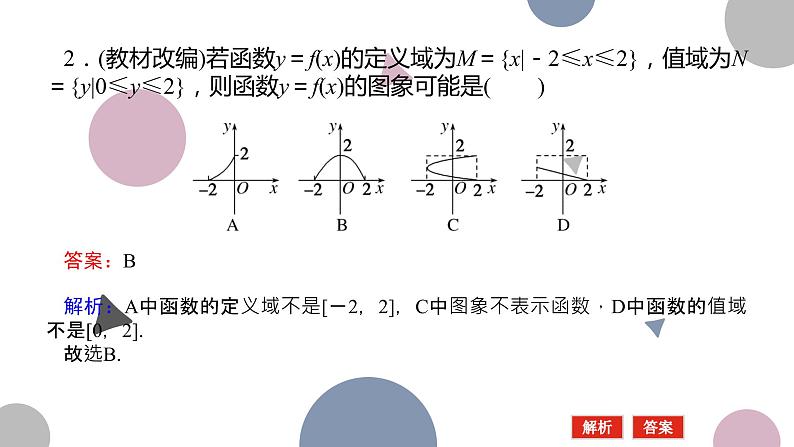
2．(教材改编)若函数y＝f(x)的定义域为M＝{x|－2≤x≤2}，值域为N＝{y|0≤y≤2}，则函数y＝f(x)的图象可能是(　　)
解析：A中函数的定义域不是[－2，2]，C中图象不表示函数，D中函数的值域不是[0，2].故选B.
解析：在A中，f(x)定义域为R，g(x)的定义域为{x|x≠0}，定义域不同，∴f(x)与g(x)不是同一函数；在B中，f(x)定义域为R，g(x)定义域为{x|x≥0}，定义域不同，∴f(x)与g(x)不是同一函数；在C中，f(x)与g(x)定义域与对应关系都相同，∴f(x)与g(x)是同一函数；在D中，f(x)与g(x)定义域都是R，但对应关系不同，∴f(x)与g(x)不是同一函数．故选C.
解析：由题意知，x≥0且2－x>0，解得0≤x＜2，故其定义域是[0，2)．故选B.
解析：∵f(a)＋f(1)＝0，∴f(a)＝－f(1)＝－2，当a>0时，2a＝－2，∴a＝－1(舍去)，当a≤0时，a＋1＝－2，∴a＝－3.
题后师说求函数定义域的策略
题后师说求函数解析式的方法
(2)已知f(x)是二次函数且f(0)＝2，f(x＋1)－f(x)＝x－1，则f(x)＝___________．
(3)若f(x)对于任意实数x恒有3f(x)－2f(－x)＝5x＋1，则f(x)＝________．
解析：(3)对∀x∈R恒有3f(x)－2f(－x)＝5x＋1，①所以有3f(－x)－2f(x)＝－5x＋1，②由①②解得f(x)＝x＋1.
题后师说分段函数问题的求解策略